ВВЕДЕНИЕ
В настоящее время как в странах СНГ, так и за дальней рубежом большое внимание уделяется исследованию эффективного резонансного туннелирования электромагнитных волн через среды, например с мелкомасштабными неоднородностями [1-3]. Доказано, что в большинстве случаев это безотражательное прохождение волн в различной среде через достаточно разные слои неоднородной среды. В частности, такие случаи рассмотрены через слой неоднородностей плазмы при отсутствии внешнего магнитного поля [3-4].
Выполненный для ряда ситуаций анализ (например, работы [2,3]) показал, что можно обеспечить безотражательное туннелирование электромагнитных волн из вакуума в неоднородный слой, несмотря на скачок диэлектрической проницаемости на границе раздела. Здесь необходимо отметить, что анализ точно решаемых моделей позволит значительно улучшить существующие представления о пространственно-временной динамике электромагнитных полей в неоднородных диэлектрических структурах с сильной пространственной дисперсией.
В данной статье рассмотрена линейная одномерная задача о резонансном туннелировании электромагнитной волны через слой газов в неоднородной среде с мелкомасштабными структурами, на примере ионосферы. Напоминаем, что случай через слой газов в неоднородной среде в первые, так как исследование работы в этом областью очень малы. Можно отметить, что наиболее простые ситуации возникают в случае прохождения электромагнитной волны (или потока частиц) в слое ионосферы без внешнего магнитного поля либо при распространении электромагнитной волны поперек однородного внешнего магнитного поля в магнитоактивном газе.
ОСНОВНЫЕ УРАВНЕНИЯ И ИХ РЕШЕНИЕ
Отметим, что на основе сказанного выше в данной работе используется точно решаемая модель уравнения Гельмгольца, а также рассмотриваются безотражательное резонансное туннелирование поперечной электромагнитной волны (или поток тяжелых частиц) через слой неоднородной среды газов с мелкомасштабными структурами.
Таким образом, при проведение анализ в данной работе оно рассматривает стандартные отношения между величинами индукции (B, H, E, D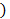 в среде:
в среде:
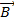 =
=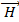 - i
- i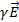 ,
, 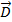 = i
= i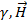 + (
+ (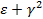 )
) 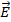 , где
, где 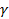 - малый параметр неоднородности.
- малый параметр неоднородности.
При распространении волны или поток частиц поперек однородного внешнего магнитного поля для волнового поля используем стандартное представление 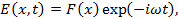 где
где 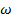 -частота волны. Тогда получаем для амплитуды волны F(x) с помощью уравнения Гельмгольца [1]:
-частота волны. Тогда получаем для амплитуды волны F(x) с помощью уравнения Гельмгольца [1]:
d2F / dx2 + k02 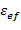 (x) F = 0, (1)
(x) F = 0, (1)
где ось x соответствует направлению неоднородности, k0 = w / c-вакуумное волновое число, ef(x)-эффективная диэлектрическая проницаемость газов. Так как в случае распространения волн в различных слоях газов без внешнего магнитного поля имеется ef(x) = 1 – [ wpe(x) / w ]2 , где wpe(x)-электронная ленгмюровская частота. Так как на практике и опыт показывает, что при распространении необыкновенной волны в магнитоактивном слое газов поперек внешнего магнитного поля можно получить ef(x) º Р2(x) = e^ - ( ec2 / e^ ). Здесь Р-показатель преломления, exx = eyy º e^ и exy = - i ec-компоненты тензора диэлектрической проницаемости газов (см., например, [4]). Для дальнейшего анализа и упрощения задачи введем переменную  = k0 x и безразмерный волновой вектор Z(
= k0 x и безразмерный волновой вектор Z( ) = c kx(x) / w . Тогда точное решение уравнения (1) записывается аналогично [2, 3] в виде
) = c kx(x) / w . Тогда точное решение уравнения (1) записывается аналогично [2, 3] в виде
F(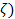 = F0 exp[ i Y(
= F0 exp[ i Y(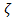 ) ] [1/ Z (
) ] [1/ Z ( )] 1/2 , dY/d
)] 1/2 , dY/d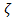 = Z (
= Z ( ), F0 = const. (2)
), F0 = const. (2)
Тогда с учетом выражениях (1) и (2) для точности решения, величина эффективной диэлектрической проницаемости ef(x), которая связана с безразмерным волновым вектором Z( ), приобретает следующее нелинейное уравнение:
), приобретает следующее нелинейное уравнение:
ef( ) = [Z(
) = [Z( ) ]2 + (d2 Z / d
) ]2 + (d2 Z / d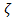 2) /2Z – 0.75(dZ / d
2) /2Z – 0.75(dZ / d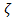 )2 /Z2. (3)
)2 /Z2. (3)
Согласно (3), в точном решении возникает некотораяе нелокальная связь функций ef( ) и Z(
) и Z( ), что является принципиальным отличием от классических соотношений. Введем также нормированную амплитуду волныôF / F0 ôº A(
), что является принципиальным отличием от классических соотношений. Введем также нормированную амплитуду волныôF / F0 ôº A( ) = [1/Z(
) = [1/Z( )]1/2. Тогда формула (3) может быть записана в виде уравнения для амплитуды волны A(
)]1/2. Тогда формула (3) может быть записана в виде уравнения для амплитуды волны A( ) с кубической нелинейностью
) с кубической нелинейностью
d2A / d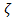 2 + ef(
2 + ef( ) A - [ 1 / A(
) A - [ 1 / A( ]3 = 0. (4)
]3 = 0. (4)
Отметим, что нелинейное уравнение (4) при заданной функции эффективной диэлектрической проницаемости ef( ) определяет пространственный профиль безразмерной амплитуды электромагнитной волны. Тогда приходим внимание к следующее. В случае однородного слоя газов, когда ef(
) определяет пространственный профиль безразмерной амплитуды электромагнитной волны. Тогда приходим внимание к следующее. В случае однородного слоя газов, когда ef( ) = const, решение уравнения (4) для фиксированной частоты волны, т.е фактически уравнение нелинейного осциллятора без диссипации, при ef(
) = const, решение уравнения (4) для фиксированной частоты волны, т.е фактически уравнение нелинейного осциллятора без диссипации, при ef( ) > 0 описывает как распространение электромагнитной волны или поток частиц в газах с постоянной амплитудой A0 = 1/ef1/4, так и пространственно модулированный волновой пакет с параметром, который определяет величину вариаций Amin < A < Amax амплитуды А, причем эти вариации могут быть и весьма большими.
) > 0 описывает как распространение электромагнитной волны или поток частиц в газах с постоянной амплитудой A0 = 1/ef1/4, так и пространственно модулированный волновой пакет с параметром, который определяет величину вариаций Amin < A < Amax амплитуды А, причем эти вариации могут быть и весьма большими.
В дальнейшем рассмотрим безотражательное прохождение поперечной электромагнитной волны через слой газов, занимающий область 0 £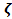 £ 3b которая слева (
£ 3b которая слева ( = 0 ) и справа (
= 0 ) и справа ( = 3b ) граничит с вакуумом. В качестве, наиболее простой аналитической модели, автоматически обеспечивающей на границах газового слоя
= 3b ) граничит с вакуумом. В качестве, наиболее простой аналитической модели, автоматически обеспечивающей на границах газового слоя  = 0,
= 0,  = 3 b, условия безотражательной сшивки полей, падающих из вакуума (
= 3 b, условия безотражательной сшивки полей, падающих из вакуума ( < 0) и уходящих вправо от газового слоя (
< 0) и уходящих вправо от газового слоя ( > 3b) электромагнитными волнами, используем следующее выражение для безразмерного волнового вектора Z(
> 3b) электромагнитными волнами, используем следующее выражение для безразмерного волнового вектора Z(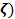 = 1 – m [1 – cos ( g
= 1 – m [1 – cos ( g  )], где m-параметр задачи (0 < m < 0.5), g = 2p / b, b -параметр толщины газового слоя, ниже он полагается равным b = 20. Входящий в данную формулу множитель [ 1 – cos ( g
)], где m-параметр задачи (0 < m < 0.5), g = 2p / b, b -параметр толщины газового слоя, ниже он полагается равным b = 20. Входящий в данную формулу множитель [ 1 – cos ( g  ) ] обеспечивает выполнение условий безотражательной сшивки полей электромагнитных волн на границах газ-вакуум, а именно p(0) = p(b) = 1, dp / d
) ] обеспечивает выполнение условий безотражательной сшивки полей электромагнитных волн на границах газ-вакуум, а именно p(0) = p(b) = 1, dp / d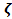 = 0 при
= 0 при  = 0,
= 0,  = 3 b.
= 3 b.
Введем обозначения g( ) = m g2 cos(g
) = m g2 cos(g ), h(
), h( ) = 0.5 / p(
) = 0.5 / p( ), q(
), q( ) = [m g sin(g
) = [m g sin(g )]2 . В итоге формулу (3) для эффективной диэлектрической проницаемости газов приводим к виду:
)]2 . В итоге формулу (3) для эффективной диэлектрической проницаемости газов приводим к виду:
ef( ) = [ p(
) = [ p( ) ]2 – g(
) ]2 – g( ) h(
) h( ) – 0.75 q(
) – 0.75 q( ) / [p
) / [p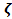 )]2 . (5)
)]2 . (5)
Численные расчеты показали, что для m < 0.49 функция ef(x) < 1, причем для m £ 0.44 она положительна. Если же m > 0.44, то в газовом слое появляются некоторые слои, в которых ef(x) отрицательно, что, по классическим представлениям, соответствует непрозрачности газов [4,5].
Более общий вариант модели газовых неоднородностей может быть описан например, [5], следующей моделью безразмерного волнового вектора p( ) = 1 – m f(
) = 1 – m f( )[1 – cos ( g
)[1 – cos ( g  )], где f(
)], где f( ) ограниченная функция (вообще говоря, произвольная), g = 2p / b - параметр толщины газового слоя. Входящий в данную формулу множитель [1 – cos ( g
) ограниченная функция (вообще говоря, произвольная), g = 2p / b - параметр толщины газового слоя. Входящий в данную формулу множитель [1 – cos ( g  )] обеспечивает выполнение условия безотражательной сшивки полей электромагнитных волн на границах газ-вакуум, а именно p(0) = p(b) = 1, dp/d
)] обеспечивает выполнение условия безотражательной сшивки полей электромагнитных волн на границах газ-вакуум, а именно p(0) = p(b) = 1, dp/d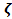 = 0 при
= 0 при  = 0,
= 0,  = b.
= b.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ И ИХ ОБСУЖДЕНИЕ
Полученные результаты можно рассматривать как применение данной функции в зависимости от параметров, а также вычисление с помощью компьютерных вычислительных программ. Поэтому в качестве примера рассмотрим следующий вариант выбора функции f( ):
):
f( ) = [ 1 + cos(2 g
) = [ 1 + cos(2 g  ) - cos(3 g
) - cos(3 g  ) – 0.5 cos(4 g
) – 0.5 cos(4 g  ) + 0.5 cos(5 g
) + 0.5 cos(5 g  ) ], (6)
) ], (6)
где m-свободный параметр задачи и выполняются условия f(0) = f(b) = 0. Используя выражение (5), вычислим по формуле (3) эффективную диэлектрическую проницаемость ef( ).
).
Рассмотрим вариант безотражательного взаимодействия электромагнитной волны с неоднородным газовым слоем при выборе более сложной функции f( ) по сравнению с выражением (5), когда
) по сравнению с выражением (5), когда
f( ) = 0.125 m [ 1 - 0.25 cos( g
) = 0.125 m [ 1 - 0.25 cos( g  ) – 0.5 cos(2 g
) – 0.5 cos(2 g  ) – 1.25 cos(3 g
) – 1.25 cos(3 g  ) – cos(4 g
) – cos(4 g  ) – 0.25 cos (5 g
) – 0.25 cos (5 g  ) – 0.5 cos(6 g
) – 0.5 cos(6 g  ) – 0.5 cos (7 g
) – 0.5 cos (7 g  ) – 0.25 cos (9 g
) – 0.25 cos (9 g  ) ], (7)
) ], (7)
При выборе данных параметров получаем вариант газов без внешнего магнитного поля, а также некоторые графики на примере пространственных профилей диэлектрической проницаемости ef( ), волнового числа p(
), волнового числа p( ) и других параметров так как эти графики показано в ниже.
) и других параметров так как эти графики показано в ниже.
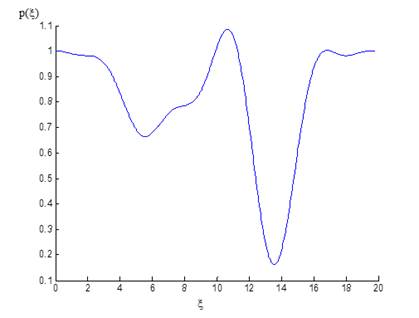
Рис.1. График зависимости p( )
)
Как видно из рисунка 1, профиль волнового вектора включает и слои непрозрачности, в которых 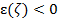 . Отметим, что вне слоев гибридного резонанса имеется корреляция максимума p(
. Отметим, что вне слоев гибридного резонанса имеется корреляция максимума p( )
)
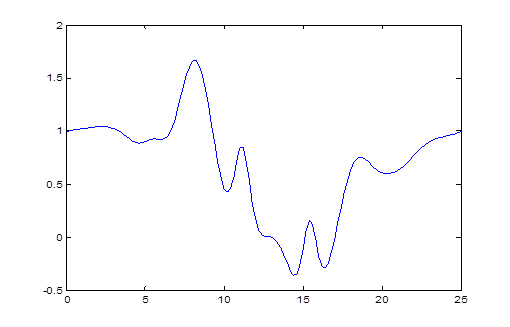
Рис. 2. График зависимости 
Так как рисунок 2 показывает, что величина пространственных профилей диэлектрической проницаемости  в неоднородном газовом слое означает, что существуют некоторые зоны непрозрачности, т.е. пространственных профилей диэлектрической проницаемости
в неоднородном газовом слое означает, что существуют некоторые зоны непрозрачности, т.е. пространственных профилей диэлектрической проницаемости 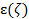 при ниже нуля создаёт зоны непрозрачности
при ниже нуля создаёт зоны непрозрачности
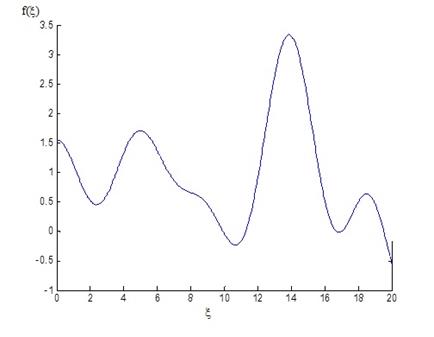
Рис. 3. График зависимости f( )
)
Как видно из рисунка 3, меняя параметры функции f( ), можно получить неограниченное количество различных профилей неоднородности в данном слое с субволновыми структурами, т.е. для которых реализуется безотражательное прохождение электромагнитных волн через среду.
), можно получить неограниченное количество различных профилей неоднородности в данном слое с субволновыми структурами, т.е. для которых реализуется безотражательное прохождение электромагнитных волн через среду.
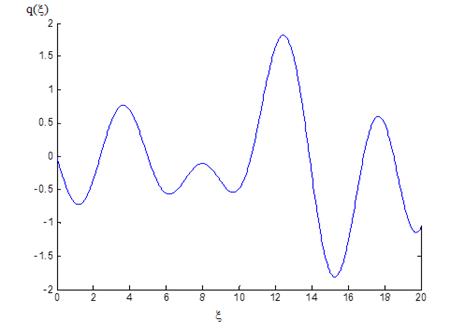
Рис. 4. График зависимости q( )
)
Как видно из рисунка 4, величина q( )-это зависимость эффективной диэлектрической проницаемости разных газов с волновым числом. Перемена линии графика завысить от параметр
)-это зависимость эффективной диэлектрической проницаемости разных газов с волновым числом. Перемена линии графика завысить от параметр 
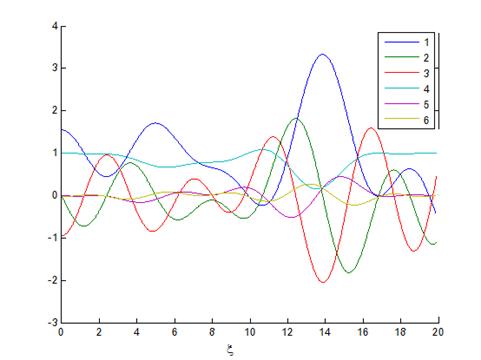
Рис.5. График в общем виде, p( ,
,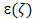 , f(
, f( ) q(
) q( ), в общем-5 параметров
), в общем-5 параметров
Как следует из сравнения на рисунке 5, в общем виде, уменьшение параметров b и 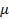 приводит к сужению зоны непрозрачности газового слоя, величина главного минимума p(
приводит к сужению зоны непрозрачности газового слоя, величина главного минимума p( ) становится несколько больше, а значение максимума ef(
) становится несколько больше, а значение максимума ef( ) уменьшается в несколько раз.
) уменьшается в несколько раз.
ЗАКЛЮЧЕНИЕ
Изучаемая выше методика исследования точных решений одномерной задачи с помощью волнового уравнения при неоднородности области газов представляет интерес, в частности, для характеристики газов и падающей из вакуума электромагнитной волны в целях существенного увеличения эффективности поглощения электромагнитного излучения в сфере газовых резонансов. Вполне очевидно, что задача о резонансном туннелировании электромагнитных волн через слой или какой-нибудь барьер представляет интерес для различных практических приложений. Исследуемые точно решаемые модели могут выявлять новые особенности в динамике волновых процессов в неоднородном газе, особенно нелинейных процессов при сильной неоднородности.
Таким образом, в настоящей работе на основе точно решаемых моделей исследованно безотражательное взаимодействие электромагнитных волн с неоднородными мелкомасштабными структурами слоя газов, на примере ионосфере. В задаче имеется ряд независимых параметров, в частности толщина неоднородного слоя, глубина модуляции диэлектрической проницаемости, величини влонового вектора и др. Меняя параметры и используя метод численные с помощью компьютерных программ можно получить зависимости графиков так как показанному выше и большое количество полностью просветленных неоднородных слоев с мелкомасштабными структурами слоя газов.
Библиографическая ссылка
Гаюров Х.Ш. О РЕЗОНАНСНОМ ТУННЕЛИРОВАНИИ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ЧЕРЕЗ НЕОДНОРОДНУЮ СРЕДУ С МЕЛКОМАСШТАБНЫМИ НЕОДНОРОДНОСТЯМИ // Научное обозрение. Фундаментальные и прикладные исследования. 2019. № 4. ;URL: https://scientificreview.ru/ru/article/view?id=69 (дата обращения: 18.11.2025).
