Обнаружение гравитационных волн ещё раз подтвердило гипотезу Луи де Бройля об универсальной двойственности корпускулярных и волновых свойств всех объектов природы.
Не обладают ли числа такой же двойственностью?
Основные формулы.
Для доказательства теории воспользуемся спиралью Феодора Киренского и прямоугольной (декартовой) системой координат.
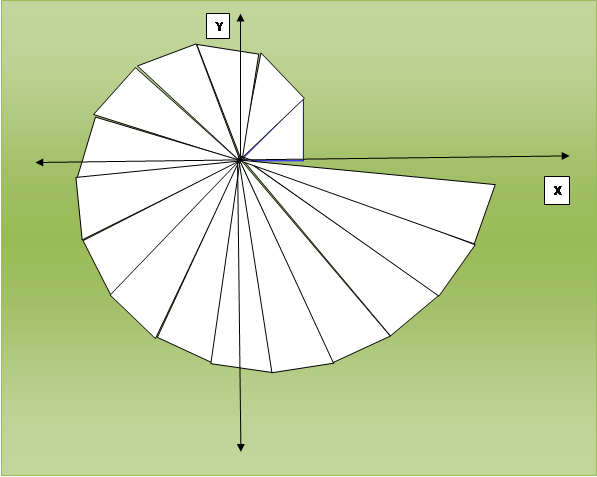
Рисунок № 1. Спираль Феодора Киренского.
Гипотенузы прямоугольных треугольников, из которых состоит спираль, равны квадратному корню из натуральных чисел от единицы до бесконечности, один из катетов всегда равен единице, второй катет последующего треугольника всегда является гипотенузой предыдущего треугольника.
Спираль Феодора Киренского наглядно показывает существование иррациональных чисел, квадратами которых являются натуральные числа, и трансцендентных чисел- углов в треугольниках, которые можно построить, но невозможно точно вычислить.
Спираль Феодора Киренского даёт возможность создать новый раздел математики – новую теорию чисел, тригонометрическую теорию чисел или волновую арифметику на основе элементарной арифметики, элементарной алгебры, геометрии и тригонометрии.
Но вернёмся к нашему доказательству.
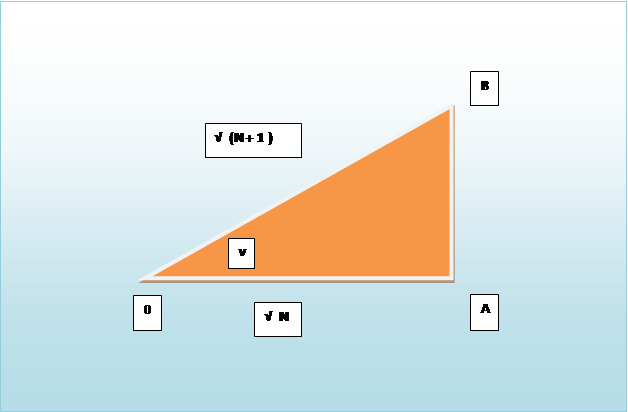
Рисунок № 2. Треугольник.
Рассмотрим какой-либо прямоугольный треугольник (рисунок № 2) из спирали Феодора Киренского.
Будем считать, что катет AB равен 1.
Катет 0A равен √N, где N – числа натурального ряда.
На основании теоремы Пифагора гипотенуза 0B равна √(N + 1).
Угол, лежащий напротив катета AB, назовём ν (ню).
Тогда тангенс угла ν равняется: tg ν = 1 / √N.
Синус угла ν равняется: sin ν = 1 / √(N + 1).
Косинус угла ν равняется: cos ν = √N / √(N + 1).
Если Ni – любое натуральное число, то на основании любого треугольника спирали Феодора Киренского получаются простые формулы – тригонометрические формулы числа:
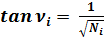 (1)
(1)
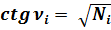 (2)
(2)
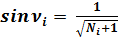 (3)
(3)
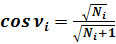 (4)
(4)
Формулы двойных углов:
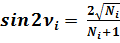 (5)
(5)
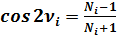 (6)
(6)
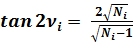 (7)
(7)
Формулы половинных углов:
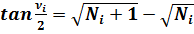 (8)
(8)
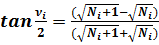 (9)
(9)
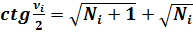 (10)
(10)
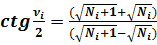 (11)
(11)
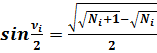 (12)
(12)
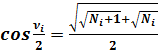 (13)
(13)
Угол ν (ню).
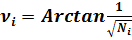 (14)
(14)
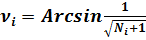 (15)
(15)
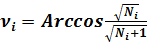 (16)
(16) 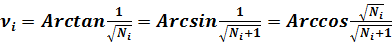
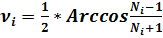 (17)
(17)
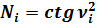 (18)
(18)
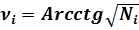 (19)
(19)
Таким образом, каждое натуральное число является квадратом котангенса угла ν, который в свою очередь равен арккотангенсу из квадратного корня данного числа.
Соответственно, любое число U есть квадрат котангенса угла u, а угол u равен: u = Arc tg ( 1 / √ U ).
Таблица № 1. Чиcла N, тангенсы угла ν, угол ν°.
|
№№ |
N |
√ N |
1 / √ N |
ν = arctg (1 / √ N) |
ν° |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
0,785398163 |
45 |
|
2 |
2 |
1,414213562 |
0,707106781 |
0,615479709 |
35,26438968 |
|
3 |
3 |
1,732050808 |
0,577350269 |
0,523598776 |
30 |
|
4 |
4 |
2 |
0,5 |
0,463647609 |
26,56505118 |
|
5 |
5 |
2,236067977 |
0,447213595 |
0,420534335 |
24,09484255 |
|
6 |
6 |
2,449489743 |
0,40824829 |
0,387596687 |
22,2076543 |
|
7 |
7 |
2,645751311 |
0,377964473 |
0,361367124 |
20,70481105 |
|
8 |
8 |
2,828427125 |
0,353553391 |
0,339836909 |
19,47122063 |
|
9 |
9 |
3 |
0,333333333 |
0,321750554 |
18,43494882 |
|
10 |
10 |
3,16227766 |
0,316227766 |
0,306277369 |
17,54840061 |
|
11 |
11 |
3,31662479 |
0,301511345 |
0,292842772 |
16,77865488 |
|
12 |
12 |
3,464101615 |
0,288675135 |
0,281034902 |
16,10211375 |
|
13 |
13 |
3,605551275 |
0,277350098 |
0,270549763 |
15,50135957 |
|
14 |
14 |
3,741657387 |
0,267261242 |
0,261157411 |
14,96321743 |
|
15 |
15 |
3,872983346 |
0,25819889 |
0,252680255 |
14,47751219 |
|
16 |
16 |
4 |
0,25 |
0,244978663 |
14,03624347 |
|
17 |
17 |
4,123105626 |
0,242535625 |
0,237941125 |
13,63302223 |
|
18 |
18 |
4,242640687 |
0,23570226 |
0,231477364 |
13,26267601 |
|
19 |
19 |
4,358898944 |
0,229415734 |
0,225513406 |
12,92096638 |
|
20 |
20 |
4,472135955 |
0,223606798 |
0,219987977 |
12,60438265 |
|
21 |
21 |
4,582575695 |
0,21821789 |
0,214849833 |
12,30998866 |
|
22 |
22 |
4,69041576 |
0,213200716 |
0,210055739 |
12,03530731 |
|
23 |
23 |
4,795831523 |
0,208514414 |
0,205568931 |
11,77823215 |
|
24 |
24 |
4,898979486 |
0,204124145 |
0,201357921 |
11,53695903 |
|
25 |
25 |
5 |
0,2 |
0,19739556 |
11,30993247 |
|
26 |
26 |
5,099019514 |
0,196116135 |
0,1936583 |
11,09580328 |
|
27 |
27 |
5,196152423 |
0,19245009 |
0,190125603 |
10,89339465 |
|
28 |
28 |
5,291502622 |
0,188982237 |
0,186779461 |
10,70167482 |
|
29 |
29 |
5,385164807 |
0,185695338 |
0,18360401 |
10,51973489 |
|
30 |
30 |
5,477225575 |
0,182574186 |
0,180585214 |
10,34677062 |
|
31 |
31 |
5,567764363 |
0,179605302 |
0,177710601 |
10,1820674 |
|
32 |
32 |
5,656854249 |
0,176776695 |
0,174969046 |
10,02498786 |
|
33 |
33 |
5,744562647 |
0,174077656 |
0,17235059 |
9,874961398 |
|
34 |
34 |
5,830951895 |
0,171498585 |
0,169846288 |
9,731475473 |
|
35 |
35 |
5,916079783 |
0,169030851 |
0,167448079 |
9,594068227 |
|
36 |
36 |
6 |
0,166666667 |
0,165148677 |
9,462322208 |
|
37 |
37 |
6,08276253 |
0,164398987 |
0,162941479 |
9,335859032 |
|
38 |
38 |
6,164414003 |
0,162221421 |
0,160820481 |
9,214334802 |
|
39 |
39 |
6,244997998 |
0,160128154 |
0,158780215 |
9,097436169 |
|
40 |
40 |
6,32455532 |
0,158113883 |
0,156815685 |
8,984876932 |
Проверка формул.
Докажем формулу:
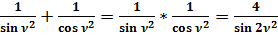 ;
;
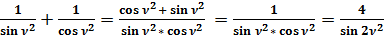
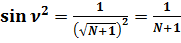 ;
;
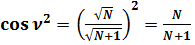 ;
;
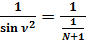 ;
;
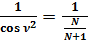 ;
;
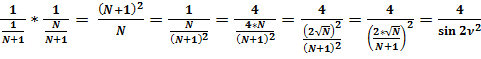 ;
;
Выводы:
Каждому числу N соответствует значение тригонометрической функции угла ν:
ctg2 νi = Ni,
или: 1 / tg2 νi = Ni
При N → ∞, угол ν → 0.
При N = 1, угол ν = π/4, или 45°.
При N → 0, угол ν → π/2, или 90°.
Вся числовая ось от нуля до бесконечности заключена между 90° и 0°.
Каждому значению числа N соответствует определённая функция угла ν.
Каждому значению угла ν соответствует определённая функция числа N.
В этом как раз и заключена двойственная природа чисел.
Угол ω (омега).
Рассмотрим рисунок № 3, где изображены первые три треугольника из спирали Феодора Киренского в координатных осях 0X и 0Y.
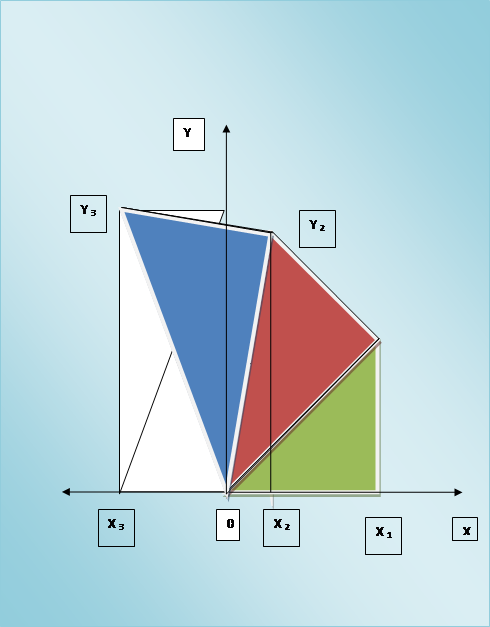
Рисунок № 3.
Ось абцисс – ось 0X.
Ось ординат– ось 0Y.
Угол B0A – ν1,
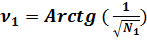
 =
=  =
= 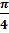 = 45°.
= 45°.
Угол B0A – ω1;
ω1 = ν1;
Угол C0B - ν2.
Угол C0A – ω2.
ω2 = ν1 + ν2.
Угол D0C – ν3.
Угол D0A – ω3.
ω3 = ν1 + ν2 + ν3.
Угол ω равен сумме углов ν:
ωi = ∑ νi.
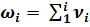 (20)
(20)
По аналогии с числами N получаем числа Ω:
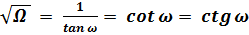 ; (21)
; (21)
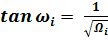 ; (22)
; (22)
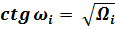 ; (23)
; (23)
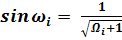 ; (24)
; (24)
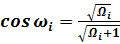 . (25)
. (25)
Таблица № 2. Чиcла N, угол ν, ω, числа Ω.
|
N = ctg² ν |
ν |
ω = Σ ν |
tg ω |
ctg ω = √ Ω |
Ω = ctg² ω |
|
|
|
|
|
|
|
|
1 |
0,785398163 |
0,785398163 |
1 |
1 |
1 |
|
2 |
0,615479709 |
1,400877872 |
5,828427125 |
0,171572875 |
0,029437252 |
|
3 |
0,523598776 |
1,924476648 |
-2,708523595 |
-0,369204832 |
0,136312208 |
|
4 |
0,463647609 |
2,388124257 |
-0,938096008 |
-1,065988972 |
1,136332489 |
|
5 |
0,420534335 |
2,808658592 |
-0,34580647 |
-2,891790888 |
8,362454542 |
|
6 |
0,387596687 |
3,196255279 |
0,054717134 |
18,27581095 |
334,0052658 |
|
7 |
0,361367124 |
3,557622403 |
0,441818923 |
2,263370689 |
5,122846874 |
|
8 |
0,339836909 |
3,897459312 |
0,942614973 |
1,060878544 |
1,125463284 |
|
9 |
0,321750554 |
4,219209866 |
1,860538922 |
0,537478678 |
0,288883329 |
|
10 |
0,306277369 |
4,525487236 |
5,287958686 |
0,18910889 |
0,035762172 |
|
11 |
0,292842772 |
4,818330007 |
-9,403873646 |
-0,106339157 |
0,011308016 |
|
12 |
0,281034902 |
5,099364909 |
-2,453841669 |
-0,407524256 |
0,166076019 |
|
13 |
0,270549763 |
5,369914672 |
-1,295088804 |
-0,772147823 |
0,59621226 |
|
14 |
0,261157411 |
5,631072083 |
-0,763544249 |
-1,309681791 |
1,715266394 |
|
15 |
0,252680255 |
5,883752338 |
-0,422124989 |
-2,368966599 |
5,612002747 |
|
16 |
0,244978663 |
6,128731001 |
-0,155694368 |
-6,422839893 |
41,25287229 |
|
17 |
0,237941125 |
6,366672126 |
0,08368133 |
11,95009688 |
142,8048154 |
|
18 |
0,231477364 |
6,59814949 |
0,325809824 |
3,069275163 |
9,420450027 |
|
19 |
0,225513406 |
6,823662896 |
0,600079003 |
1,666447244 |
2,777046416 |
|
20 |
0,219987977 |
7,043650873 |
0,951337991 |
1,051151125 |
1,104918688 |
|
21 |
0,214849833 |
7,258500706 |
1,475964614 |
0,677523018 |
0,45903744 |
|
22 |
0,210055739 |
7,468556445 |
2,464771536 |
0,405717116 |
0,164606378 |
|
23 |
0,205568931 |
7,674125376 |
5,499913818 |
0,181821031 |
0,033058887 |
|
24 |
0,201357921 |
7,875483297 |
-46,50086284 |
-0,021504977 |
0,000462464 |
|
25 |
0,19739556 |
8,072878857 |
-4,495154089 |
-0,222461784 |
0,049489246 |
|
26 |
0,1936583 |
8,266537157 |
-2,284811525 |
-0,437672862 |
0,191557534 |
|
27 |
0,190125603 |
8,456662761 |
-1,453319254 |
-0,688080061 |
0,47345417 |
|
28 |
0,186779461 |
8,643442222 |
-0,99190798 |
-1,008158035 |
1,016382624 |
|
29 |
0,18360401 |
8,827046232 |
-0,680812042 |
-1,468834184 |
2,157473861 |
|
30 |
0,180585214 |
9,007631446 |
-0,443154345 |
-2,256550141 |
5,09201854 |
|
31 |
0,177710601 |
9,185342047 |
-0,244118918 |
-4,096364219 |
16,78019982 |
|
32 |
0,174969046 |
9,360311093 |
-0,064556324 |
-15,4903491 |
239,9509154 |
|
33 |
0,17235059 |
9,532661683 |
0,108304229 |
9,233249798 |
85,25290184 |
|
287 |
0,058959719 |
31,79316172 |
0,396210363 |
2,52391177 |
6,370130625 |
|
288 |
0,058857506 |
31,85201923 |
0,466015966 |
2,145849227 |
4,604668904 |
|
289 |
0,058755823 |
31,91077505 |
0,539632275 |
1,853113771 |
3,434030647 |
|
290 |
0,058654665 |
31,96942972 |
0,617935625 |
1,618291548 |
2,618867535 |
|
|
|
|
|
|
|
|
Σ |
31,96942972 |
6012,943228 |
217,1195483 |
-745,4382655 |
327755,5451 |
|
|
|
|
|
|
|
|
N |
ν |
ω = Σ ν |
tg ω |
ctg ω = √ Ω |
Ω = ctg² ω |
Из формулы (23): 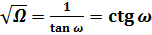 , получаем:
, получаем:
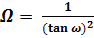 ; (26)
; (26)
На основании рисунка № 3 получаем:
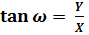 ; (27)
; (27)
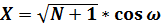 ; (28)
; (28)
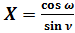 ; (29)
; (29)
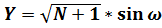 ; (30)
; (30)
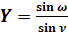 ; (31)
; (31)
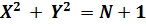 ; (32)
; (32)
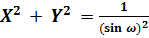 ; (33)
; (33)
Таблица № 3. Чиcла N, X, Y.
|
N |
X = cos ω / sin ν |
Y = sin ω / sin ν |
X² |
Y² |
X² + Y² = N + 1 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
2 |
|
2 |
0,292893219 |
1,707106781 |
0,085786438 |
2,914213562 |
3 |
|
3 |
-0,692705341 |
1,87620876 |
0,479840689 |
3,520159311 |
4 |
|
4 |
-1,630809721 |
1,529856089 |
2,659540345 |
2,340459655 |
5 |
|
5 |
-2,314982163 |
0,800535811 |
5,359142416 |
0,640857584 |
6 |
|
6 |
-2,641799539 |
-0,1445517 |
6,979104806 |
0,020895194 |
7 |
|
7 |
-2,587164132 |
-1,143058071 |
6,693418247 |
1,306581753 |
8 |
|
8 |
-2,183032076 |
-2,057758722 |
4,765629044 |
4,234370956 |
9 |
|
9 |
-1,497112502 |
-2,78543608 |
2,241345843 |
7,758654157 |
10 |
|
10 |
-0,616280273 |
-3,258864622 |
0,379801375 |
10,62019863 |
11 |
|
11 |
0,366304381 |
-3,444680116 |
0,1341789 |
11,8658211 |
12 |
|
12 |
1,360697877 |
-3,338937149 |
1,851498713 |
11,14850129 |
13 |
|
13 |
2,286752423 |
-2,96154746 |
5,229236645 |
8,770763355 |
14 |
|
14 |
3,078259275 |
-2,350387167 |
9,475680165 |
5,524319835 |
15 |
|
15 |
3,685126632 |
-1,55558404 |
13,5801583 |
2,419841705 |
16 |
|
16 |
4,074022642 |
-0,634302382 |
16,59766049 |
0,402339512 |
17 |
|
17 |
4,227863567 |
0,353793246 |
17,87483034 |
0,125169661 |
18 |
|
18 |
4,144473699 |
1,350310245 |
17,17666224 |
1,823337759 |
19 |
|
19 |
3,834691283 |
2,301117721 |
14,70485724 |
5,295142764 |
20 |
|
20 |
3,320145718 |
3,158580759 |
11,02336759 |
9,97663241 |
21 |
|
21 |
2,630886889 |
3,883095953 |
6,921565822 |
15,07843418 |
22 |
|
22 |
1,80300805 |
4,444002922 |
3,250838029 |
19,74916197 |
23 |
|
23 |
0,876369385 |
4,819956089 |
0,768023299 |
23,2319767 |
24 |
|
24 |
-0,107500032 |
4,998844241 |
0,011556257 |
24,98844374 |
25 |
|
25 |
-1,10726888 |
4,977344234 |
1,226044373 |
24,77395563 |
26 |
|
26 |
-2,083406395 |
4,760190941 |
4,340582205 |
22,65941779 |
27 |
|
27 |
-2,999505568 |
4,359239193 |
8,997033654 |
19,00296635 |
28 |
|
28 |
-3,823324341 |
3,792385923 |
14,61780901 |
14,38219099 |
29 |
|
29 |
-4,527552727 |
3,082412416 |
20,4987337 |
9,501266304 |
30 |
|
30 |
-5,090321664 |
2,255798163 |
25,91137465 |
5,088625354 |
31 |
|
31 |
-5,495474975 |
1,341549403 |
30,2002452 |
1,799754802 |
32 |
|
32 |
-5,732629645 |
0,370077498 |
32,86304265 |
0,136957355 |
33 |
|
33 |
-5,797051868 |
-0,627845233 |
33,60581036 |
0,394189636 |
34 |
|
287 |
15,77730497 |
6,251131736 |
248,923352 |
39,07664798 |
288 |
|
288 |
15,4089535 |
7,180818347 |
237,4358479 |
51,56415213 |
289 |
|
289 |
14,98655242 |
8,087227376 |
224,5967534 |
65,40324663 |
290 |
|
290 |
14,51165407 |
8,967268036 |
210,588104 |
80,41189603 |
291 |
|
|
|
|
|
|
|
|
Σ |
172,8585736 |
-233,1718836 |
22406,53021 |
20078,46979 |
42485 |
|
|
|
|
|
|
|
|
N |
X = cos ω / sin ν |
Y = sin ω / sin ν |
X² |
Y² |
X² + Y² = N + 1 |
Доказательство:
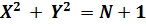 ;
;
Продифференцируем нашу формулу:
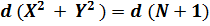 ;
;
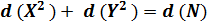 ;
;
На основании формул дифференцирования значения 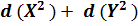 должны быть:
должны быть:
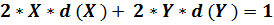 - если N – функция;
- если N – функция;
или: 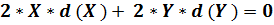 - если N – число.
- если N – число.
Вычислим дифференциал 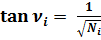 .
.
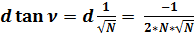 ; (34)
; (34)
Так как 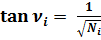 , то
, то 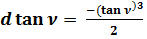 . (35)
. (35)
Соответственно, 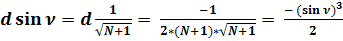 . (36)
. (36)
Общепринятые значения дифференциалов:
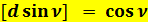 ;
;
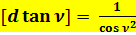 .
.
Вычислим значения sin ν, Δ sin ν, d sin ν, cos ν, значения сведём в таблицу № 4, где:
Δ ν = ν2 – ν1;
Δ sin ν = sin ν2 – sin ν1:
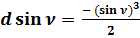 .
.
Таблица №4. Значения ν, Δ sin ν, d sin ν.
|
N |
Δ ν |
Δ (sin ν) |
d (sin ν) = -sin³ ν / 2 |
Δ (sin ν) |
d (sin ν) = cos ν |
|
|
|
|
|
|
|
|
1 |
0,785398163 |
|
-0,176776695 |
0 |
0,707106781 |
|
2 |
-0,169918455 |
-0,129756512 |
-0,096225045 |
-0,129756512 |
0,816496581 |
|
3 |
-0,091880933 |
-0,077350269 |
-0,0625 |
-0,077350269 |
0,866025404 |
|
4 |
-0,059951167 |
-0,052786405 |
-0,04472136 |
-0,052786405 |
0,894427191 |
|
5 |
-0,043113274 |
-0,038965305 |
-0,034020691 |
-0,038965305 |
0,912870929 |
|
6 |
-0,032937649 |
-0,030283817 |
-0,026997462 |
-0,030283817 |
0,9258201 |
|
7 |
-0,026229563 |
-0,024411082 |
-0,022097087 |
-0,024411082 |
0,935414347 |
|
8 |
-0,021530214 |
-0,020220057 |
-0,018518519 |
-0,020220057 |
0,942809042 |
|
9 |
-0,018086355 |
-0,017105567 |
-0,015811388 |
-0,017105567 |
0,948683298 |
|
10 |
-0,015473185 |
-0,014716421 |
-0,013705061 |
-0,014716421 |
0,953462589 |
|
11 |
-0,013434597 |
-0,01283621 |
-0,012028131 |
-0,01283621 |
0,957427108 |
|
12 |
-0,01180787 |
-0,011325036 |
-0,010667311 |
-0,011325036 |
0,960768923 |
|
13 |
-0,010485139 |
-0,010088856 |
-0,009545044 |
-0,010088856 |
0,963624112 |
|
14 |
-0,009392352 |
-0,009062352 |
-0,00860663 |
-0,009062352 |
0,966091783 |
|
15 |
-0,008477156 |
-0,00819889 |
-0,0078125 |
-0,00819889 |
0,968245837 |
|
16 |
-0,007701592 |
-0,007464375 |
-0,007133401 |
-0,007464375 |
0,9701425 |
|
17 |
-0,007037538 |
-0,006833365 |
-0,006547285 |
-0,006833365 |
0,971825316 |
|
18 |
-0,006463761 |
-0,006286527 |
-0,006037256 |
-0,006286527 |
0,973328527 |
|
19 |
-0,005963958 |
-0,005808936 |
-0,00559017 |
-0,005808936 |
0,974679434 |
|
20 |
-0,005525429 |
-0,005388908 |
-0,005195664 |
-0,005388908 |
0,975900073 |
|
21 |
-0,005138144 |
-0,005017174 |
-0,004845471 |
-0,005017174 |
0,977008421 |
|
22 |
-0,004794094 |
-0,004686302 |
-0,004532922 |
-0,004686302 |
0,978019294 |
|
23 |
-0,004486808 |
-0,004390269 |
-0,004252586 |
-0,004390269 |
0,97894501 |
|
24 |
-0,00421101 |
-0,004124145 |
-0,004 |
-0,004124145 |
0,979795897 |
|
25 |
-0,003962361 |
-0,003883865 |
-0,003771464 |
-0,003883865 |
0,980580676 |
|
26 |
-0,003737259 |
-0,003666045 |
-0,003563891 |
-0,003666045 |
0,981306763 |
|
27 |
-0,003532697 |
-0,003467853 |
-0,003374683 |
-0,003467853 |
0,981980506 |
|
28 |
-0,003346142 |
-0,003286898 |
-0,003201644 |
-0,003286898 |
0,982607369 |
|
29 |
-0,003175451 |
-0,003121152 |
-0,003042903 |
-0,003121152 |
0,98319208 |
|
30 |
-0,003018796 |
-0,002968884 |
-0,00289686 |
-0,002968884 |
0,983738754 |
|
31 |
-0,002874613 |
-0,002828607 |
-0,002762136 |
-0,002828607 |
0,984250984 |
|
32 |
-0,002741555 |
-0,002699039 |
-0,00263754 |
-0,002699039 |
0,984731928 |
|
33 |
-0,002618456 |
-0,002579071 |
-0,002522038 |
-0,002579071 |
0,985184366 |
|
287 |
-0,000102747 |
-0,000102569 |
-0,000102301 |
-0,000102569 |
0,998262379 |
|
288 |
-0,000102213 |
-0,000102036 |
-0,000101771 |
-0,000102036 |
0,998268397 |
|
289 |
-0,000101683 |
-0,000101507 |
-0,000101245 |
-0,000101507 |
0,998274373 |
|
290 |
-0,000101158 |
-0,000100984 |
-0,000100723 |
-0,000100984 |
0,998280308 |
|
|
|
|
|
|
|
|
Σ |
0,058654665 |
-0,648485743 |
-0,747616955 |
-0,648485743 |
287,2762485 |
|
|
|
|
|
|
|
|
N |
Δ ν |
Δ (sin ν) |
d (sin ν) = -sin³ ν / 2 |
Δ (sin ν) |
d (sin ν) = cos ν |
С увеличением N значения Δ sin ν и d sin ν становятся практически равными, в отличие от общепринятого значения.
Аналогичные значения получаются и при сравнении Δ cos ν и d cos ν, Δ tg ν и d tg ν, Δ ctg ν и d ctg ν.
Вывод: общепринятые значения дифференциалов тригонометрических функций подсчитаны не правильно.
Соответственно, не правильно подсчитаны общепринятые значения интегралов тригонометрических функций.
На основании ранее полученных формул, получим следующие формулы:
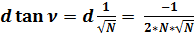 ;
; 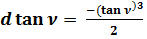 ; (35)
; (35)
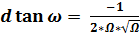 ;
; 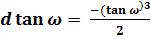 ; (37)
; (37)
d (ctg ν) = 1 / (2 * √ N) = tg ν / 2 = 1 / (2 *ctg ν) (38)
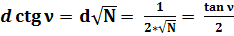 ; (39)
; (39)
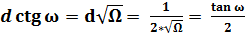 ; (40)
; (40)
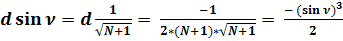 ; (36)
; (36)
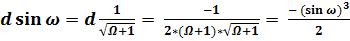 ; (41)
; (41)
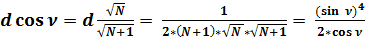 ; (42)
; (42)
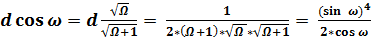 ; (43)
; (43)
Отношения полученных значений дифференциалов к общепринятым:
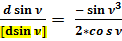 ;
;
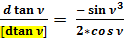 ;
;
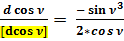 ;
;
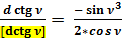 ;
;

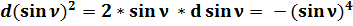 ; (44)
; (44)
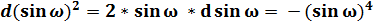 ; (45)
; (45)
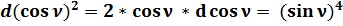 ; (46)
; (46)
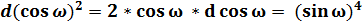 ; (47)
; (47)
Проверка полученных формул:
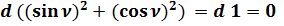 ;
;
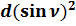 +
+ 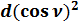 =
= 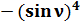 +
+ 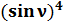 = 0;
= 0;
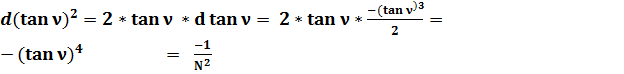 ; (48)
; (48)
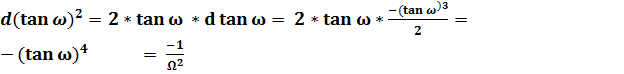 ; (49)
; (49)
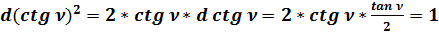 ;
;
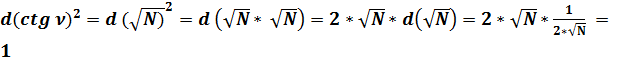 ;
;
Разница чисел: Δ N = N + 1 – N = 1;
Δ N = d (ctg² ν) = 1.
Общепринятое значение:
 ;
;
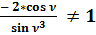 .
.
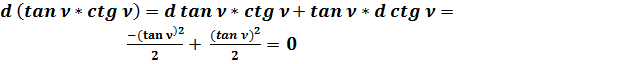 ;
;
Общепринятое значение:
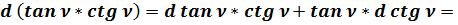
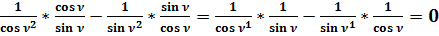 .
.
Соответственно, для угла ω:
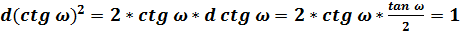 ;
;
Общепринятое значение:
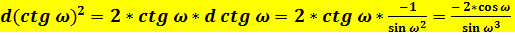 ;
;
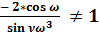 .
.
Проверка значений:
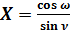 ;
; 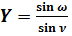 .
.
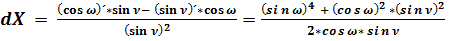 ; (50)
; (50)
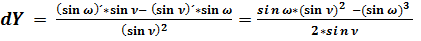 ; (51)
; (51)
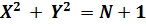 ;
;
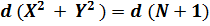 ;
;
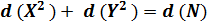 ;
;
Должно быть:
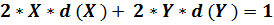 ;
;
или: 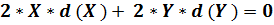 .
.
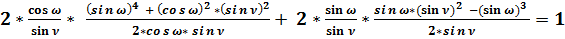 ;
;
Таблица № 5. Значения 2 * X * d (X ) + 2 * Y * d ( Y ).
|
d ( X ) = (sin4 ω + cos² ω * sin² ν) / (2 * cos ω * sin ν) |
d ( Y ) = (sin ω * sin² ν - sin³ ω)/(2 * sin ν) |
2 * X * d ( X ) |
2 * Y * d ( Y ) |
2 * X * d ( X ) + + 2 * Y * d ( Y ) |
|
|
|
|
|
|
|
0,5 |
0 |
1 |
0 |
1 |
|
4,881430372 |
-0,544627825 |
2,859475708 |
-1,859475708 |
1 |
|
-2,322661871 |
-0,591043122 |
3,217840566 |
-2,217840566 |
1 |
|
-0,498972482 |
-0,205071037 |
1,627458348 |
-0,627458348 |
1 |
|
-0,207699255 |
0,023958864 |
0,961640143 |
0,038359857 |
1 |
|
-0,188711772 |
-0,010109376 |
0,997077345 |
0,002922655 |
1 |
|
-0,202938761 |
0,021902547 |
1,050071765 |
-0,050071765 |
1 |
|
-0,577574005 |
0,369753058 |
2,52172516 |
-1,52172516 |
1 |
|
-2,085282839 |
0,941289957 |
6,243806017 |
-5,243806017 |
1 |
|
-8,346882623 |
1,425042044 |
10,2880382 |
-9,288038201 |
1 |
|
16,0308267 |
1,559553245 |
11,74432411 |
-10,74432411 |
1 |
|
3,56549447 |
1,303277229 |
9,703121512 |
-8,703121512 |
1 |
|
1,283097338 |
0,82191016 |
5,868251891 |
-4,868251891 |
1 |
|
0,433077986 |
0,354463443 |
2,666252654 |
-1,666252654 |
1 |
|
0,164816183 |
0,069021347 |
1,214737011 |
-0,214737011 |
1 |
|
0,120992841 |
-0,011149926 |
0,985855151 |
0,014144849 |
1 |
|
0,117543592 |
0,008597474 |
0,993916544 |
0,006083456 |
1 |
|
0,130174759 |
-0,029256879 |
1,079011728 |
-0,079011728 |
1 |
|
0,27866255 |
-0,247090728 |
2,137169706 |
-1,137169706 |
1 |
|
0,792826374 |
-0,675081391 |
5,264598182 |
-4,264598182 |
1 |
|
2,023865931 |
-1,242452518 |
10,64912469 |
-9,649124685 |
1 |
|
4,741837043 |
-1,811333274 |
17,09914072 |
-16,09914072 |
1 |
|
12,84876689 |
-2,232440656 |
22,52053186 |
-21,52053186 |
1 |
|
-116,17371 |
-2,398289877 |
24,97735508 |
-23,97735508 |
1 |
|
-10,68073077 |
-2,275599249 |
23,65288161 |
-22,65288161 |
1 |
|
-4,602414569 |
-1,909314155 |
19,17739989 |
-18,17739989 |
1 |
|
-2,20339745 |
-1,401414937 |
13,21820584 |
-12,21820584 |
1 |
|
-0,998703127 |
-0,875007461 |
7,636731952 |
-6,636731952 |
1 |
|
-0,407772888 |
-0,436740147 |
3,692426503 |
-2,692426503 |
1 |
|
-0,164149214 |
-0,148759896 |
1,671144601 |
-0,671144601 |
1 |
|
-0,095076411 |
-0,016764228 |
1,04498008 |
-0,04498008 |
1 |
|
-0,086907601 |
0,004839283 |
0,996418181 |
0,003581819 |
1 |
|
-0,085644943 |
-0,005593458 |
0,992976348 |
0,007023652 |
1 |
|
-0,098657799 |
0,037793007 |
1,122602889 |
-0,122602889 |
1 |
|
-0,189506605 |
0,20366704 |
2,052433835 |
-1,052433835 |
1 |
|
0,517956468 |
-0,898006378 |
15,52476353 |
-14,52476353 |
1 |
|
0,79053196 |
-1,223552847 |
22,94385267 |
-21,94385267 |
1 |
|
|
|
|
|
|
|
1837,033778 |
89,89744322 |
15026,99231 |
-14736,99231 |
290 |
|
|
|
|
|
|
|
d ( X ) = (sin4 ω + cos² ω * sin² ν) / (2 * cos ω * sin ν) |
d ( Y ) = (sin ω * sin² ν - sin³ ω) / (2 * sin ν) |
2 * X * d ( X ) |
2 * Y * d ( Y ) |
2 * X * d ( X ) + + 2 * Y * d ( Y ) |
Общепринятое значение:
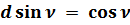 ;
; 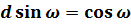 ;
;
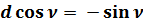 ;
; 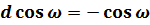 ;
;
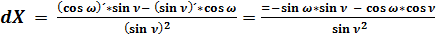 ; (52)
; (52)
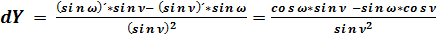 ; (53)
; (53)
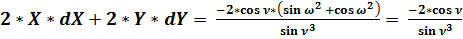 .
.
Таблица № 6. Значения 2 * X * d (X ) + 2 * Y * d ( Y ) при общепринятых значениях.
|
N |
2 * X * d ( X ) |
2 * Y * d ( Y ) |
2 * X * d ( X ) + 2 * Y * d ( Y ) |
(-2 )* cos ν / sin³ ν |
|
|
|
|
|
|
|
1 |
-4 |
0 |
-4 |
-4 |
|
2 |
-1,242640687 |
-7,242640687 |
-8,485281374 |
-8,485281374 |
|
3 |
0,93710275 |
-14,79350921 |
-13,85640646 |
-13,85640646 |
|
4 |
-5,648353017 |
-14,35164698 |
-20 |
-20 |
|
5 |
-20,26036124 |
-6,57245449 |
-26,83281573 |
-26,83281573 |
|
6 |
-34,9542445 |
0,661388102 |
-34,2928564 |
-34,2928564 |
|
7 |
-41,33279789 |
-0,999223088 |
-42,33202098 |
-42,33202098 |
|
8 |
-35,94277549 |
-14,96891275 |
-50,91168825 |
-50,91168825 |
|
9 |
-21,78829742 |
-38,21170258 |
-60 |
-60 |
|
10 |
-6,418822763 |
-63,15128576 |
-69,57010852 |
-69,57010852 |
|
11 |
1,633560706 |
-81,23255567 |
-79,59899497 |
-79,59899497 |
|
12 |
-3,740989982 |
-86,32565201 |
-90,06664199 |
-90,06664199 |
|
13 |
-24,16391005 |
-76,79152566 |
-100,9554357 |
-100,9554357 |
|
14 |
-56,43929517 |
-55,81042643 |
-112,2497216 |
-112,2497216 |
|
15 |
-93,72640548 |
-30,2090616 |
-123,9354671 |
-123,9354671 |
|
16 |
-127,6129594 |
-8,387040623 |
-136 |
-136 |
|
17 |
-150,3912062 |
1,959403684 |
-148,4318025 |
-148,4318025 |
|
18 |
-156,9414628 |
-4,27888333 |
-161,2203461 |
-161,2203461 |
|
19 |
-145,8421255 |
-28,51383227 |
-174,3559577 |
-174,3559577 |
|
20 |
-119,5698939 |
-68,25981625 |
-187,8297101 |
-187,8297101 |
|
21 |
-83,86917108 |
-117,7641595 |
-201,6333306 |
-201,6333306 |
|
22 |
-46,52070993 |
-169,238415 |
-215,759125 |
-215,759125 |
|
23 |
-15,8147446 |
-214,3851685 |
-230,1999131 |
-230,1999131 |
|
24 |
0,961524101 |
-245,9104984 |
-244,9489743 |
-244,9489743 |
|
25 |
-1,237926976 |
-258,762073 |
-260 |
-260 |
|
26 |
-24,43060224 |
-250,9164515 |
-275,3470537 |
-275,3470537 |
|
27 |
-67,34879197 |
-223,6357437 |
-290,9845357 |
-290,9845357 |
|
28 |
-125,7013066 |
-181,2058455 |
-306,9071521 |
-306,9071521 |
|
29 |
-192,8665491 |
-130,2433393 |
-323,1098884 |
-323,1098884 |
|
30 |
-260,8794113 |
-78,70857438 |
-339,5879857 |
-339,5879857 |
|
31 |
-321,5507956 |
-34,78612364 |
-356,3369192 |
-356,3369192 |
|
32 |
-367,5598504 |
-5,792530065 |
-373,3523805 |
-373,3523805 |
|
33 |
-393,3806686 |
2,750408639 |
-390,63026 |
-390,63026 |
|
34 |
-395,9410252 |
-12,22560744 |
-408,1666326 |
-408,1666326 |
|
35 |
-374,9540315 |
-51,0037129 |
-425,9577444 |
-425,9577444 |
|
36 |
-332,9080691 |
-111,0919309 |
-444 |
-444 |
|
37 |
-274,7407837 |
-187,5491686 |
-462,2899523 |
-462,2899523 |
|
288 |
-8280,137702 |
-1528,847567 |
-9808,985269 |
-9808,985269 |
|
289 |
-7878,688928 |
-1981,311072 |
-9860 |
-9860 |
|
290 |
-7432,632157 |
-2478,470708 |
-9911,102865 |
-9911,102865 |
|
|
|
|
|
|
|
42195 |
-617650,492 |
-539630,6657 |
-1157281,158 |
-11,71276549 |
|
|
|
|
|
|
|
N |
2 * X * d ( X ) |
2 * Y * d ( Y ) |
2 * X * d ( X ) + 2 * Y * d ( Y ) |
(-2 )* cos ν / sin³ ν |
Но значения 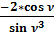 являются ни чем иным, как отношениями значений общепринятых дифференциалов к значениям дифференциалам, полученных нами.
являются ни чем иным, как отношениями значений общепринятых дифференциалов к значениям дифференциалам, полученных нами.
Значения по таблице № 6 не равны ни 0, ни 1, что однозначно доказывает, что общепринятые формулы дифференцирования тригонометрических функций определены не правильно.
2. Проверка значений:
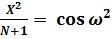 ; (53)
; (53)
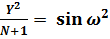 . (54)
. (54)
Продифференцируем значения (53) и (54):
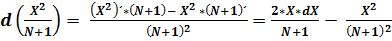 ; (55)
; (55)
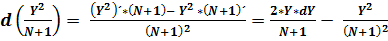 ; (56)
; (56)
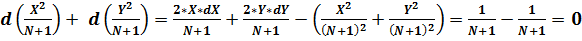 .
.
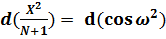 ;
;
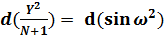 ;
;
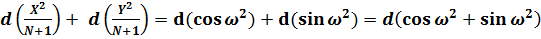 .
.
Таким образом, если числа N является функцией, значения d (cos² ω + sin² ω) равны 0, что и требовалось доказать.
В таблице № 7 представлены значения d (X2 / (N + 1)) и d (Y2 / (N + 1)).
Таблица № 7. Значения d (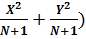 .
.
|
N |
2 * X * d ( X ) / (N + 1) - -X² / (N + 1)² |
2 * Y * d ( Y ) / (N + 1) - - Y² / (N + 1)² |
2 * X * d ( X ) / (N + 1)- - X² / (N + 1)² + |
|
|
|
|
+ 2 * Y * d ( Y ) / (N + 1) - - Y² / (N + 1)² |
|
1 |
0,25 |
-0,25 |
0 |
|
2 |
0,943626743 |
-0,943626743 |
0 |
|
3 |
0,774470098 |
-0,774470098 |
0 |
|
4 |
0,219110056 |
-0,219110056 |
0 |
|
5 |
0,01140829 |
-0,01140829 |
0 |
|
6 |
8,91039E-06 |
-8,91039E-06 |
1,51246E-17 |
|
7 |
0,026674311 |
-0,026674311 |
0 |
|
8 |
0,221356758 |
-0,221356758 |
0 |
|
9 |
0,601967143 |
-0,601967143 |
0 |
|
10 |
0,932137346 |
-0,932137346 |
0 |
|
11 |
0,977761878 |
-0,977761878 |
0 |
|
12 |
0,735438349 |
-0,735438349 |
0 |
|
13 |
0,392481071 |
-0,392481071 |
0 |
|
14 |
0,135636043 |
-0,135636043 |
0 |
|
15 |
0,02287357 |
-0,02287357 |
0 |
|
16 |
0,000560128 |
-0,000560128 |
0 |
|
17 |
4,83563E-05 |
-4,83563E-05 |
-8,18573E-18 |
|
18 |
0,009209309 |
-0,009209309 |
1,73472E-17 |
|
19 |
0,070096342 |
-0,070096342 |
0 |
|
20 |
0,225698853 |
-0,225698853 |
0 |
|
21 |
0,469750366 |
-0,469750366 |
0 |
|
22 |
0,737295649 |
-0,737295649 |
0 |
|
23 |
0,937022121 |
-0,937022121 |
0 |
|
24 |
0,999075713 |
-0,999075713 |
0 |
|
25 |
0,907912541 |
-0,907912541 |
0 |
|
26 |
0,704319911 |
-0,704319911 |
0 |
|
27 |
0,460602972 |
-0,460602972 |
0 |
|
28 |
0,245954123 |
-0,245954123 |
0 |
|
29 |
0,100304513 |
-0,100304513 |
0 |
|
30 |
0,026944961 |
-0,026944961 |
0 |
|
31 |
0,003163201 |
-0,003163201 |
6,07153E-18 |
|
32 |
1,72243E-05 |
-1,72243E-05 |
-6,58653E-18 |
|
33 |
0,000134416 |
-0,000134416 |
1,21702E-17 |
|
34 |
0,005650683 |
-0,005650683 |
-1,56125E-17 |
|
35 |
0,034385173 |
-0,034385173 |
0 |
|
287 |
0,018409824 |
-0,018409824 |
0 |
|
288 |
0,03183465 |
-0,03183465 |
0 |
|
289 |
0,050863076 |
-0,050863076 |
0 |
|
290 |
0,076358014 |
-0,076358014 |
0 |
|
N |
2 * X * d ( X ) / (N + 1) - -X² / (N + 1)² |
2 * Y * d ( Y ) / (N + 1) - - Y² / (N + 1)² |
2 * X * d ( X ) / (N + 1)- - X² / (N + 1)² + |
|
|
|
|
+ 2 * Y * d ( Y ) / (N + 1) - - Y² / (N + 1)² |
Если числа N является функцией, значения d (cos² ω + sin² ω) равны 0.
Общепринятое значение:
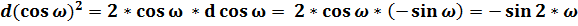 ;
;
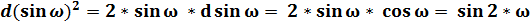 ;
;
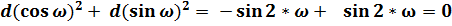 .
.
Значения d (cos² ω + sin² ω) всегда равны 0 при общепринятых значениях дифференциалов тригонометрических функций и только при условии, что числа N являются функцией угла.
Таким образом, числа обладают двойственной природой: числа являются числами и функциями углов, - что и требовалось доказать.
Заключение.
Доказательство двойственной природы числа всего лишь часть новой теории чисел – тригонометрической теории чисел или, как я её называю, волновой теории чисел или волновой арифметики.
Волновая теория чисел наконец-то позволяет, в отличие от общепринятых теорий, включая и высшую математику, точно, а не приблизительно производить всевозможные расчёты, то есть делать то, для чего и предназначена математика.
