Введение
Решение основной проблемы материаловедения – получение материалов с заранее заданными свойствами – может быть сделано лишь на основе фундаментальных принципов, определяющих совокупность физико-химических критериев данного вещества. Несомненно, таким базисом являются квантово-механические представления физики и химии твердого тела. С другой стороны, можно констатировать, что к настоящему времени накоплен значительный объем экспериментального материала по физико-химическим свойствам многих соединений. Хотя и имеется ряд полуэмпирических моделей по обработке этой информации, тем не менее, еще отсутствует теоретическое обоснование направления научных поисков для решения таких физико-химических проблем. Да и сами такие поиски часто ведутся интуитивно, методом "проб и ошибок". Аналогичные трудности возникают и при практическом использовании (в тех же целях) статистической модели атома Томаса-Ферми-Дирака. Одной из возможных причин такого несоответствия, по нашему мнению, является недостаточный учет суммарного паритетного соотношения противоположных энтропийных составляющих структурных взаимодействий.
Для получения зависимости между энергетическими параметрами свободных атомов и степенью структурных взаимодействий в простых и сложных системах классическая физика и квантовая механика широко используют кулоновские взаимодействия и их разновидности. Но биологические и многие кластерные системы в структурной основе электронейтральные. И для них основное значение имеют равновесно-обменные пространственно-энергетические взаимодействия не кулоновского типа.
В данной работе развит метод, основанный на применении пространственно-энергетического критерия (Р-параметра). Этот критерий найден и обоснован, исходя из энтропийной методологии суммирования обратных величин составляющих энергий разноименно заряженных систем. Р-параметр, рассчитанный по этим правилам для атома, приобретает физический смысл максимально эффективной энергии атома, т.е. энергии, ответственной за межатомные взаимодействия.
Поскольку Р-параметр включает в себя основные факторы, характеризующие стабильное состояние атома, то с его помощью удается скоррелировать, а, следовательно, и предсказать многие физико-химические свойства соединений и установить энергетические критерии структурных взаимодействий, взаимной растворимости систем, образования стабильных фаз и т.д.
2. Исходные принципы
Был проведен [1] анализ характера изменения величины потенциальной энергии 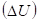 по ее знаку для различных потенциальных полей (таблица 1).
по ее знаку для различных потенциальных полей (таблица 1).
Получено, что значения –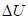 и соответственно
и соответственно 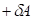 (положительная работа) соответствуют взаимодействиям, происходящим по градиенту потенциала, а +
(положительная работа) соответствуют взаимодействиям, происходящим по градиенту потенциала, а +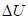 и
и 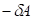 (отрицательная работа) имеют место при взаимодействиях против градиента потенциала.
(отрицательная работа) имеют место при взаимодействиях против градиента потенциала.
Таблица 1 – Направленность процессов взаимодействий
|
№ п/п |
Системы |
Вид потенциального поля |
Процесс |
|
|
|
Знак
|
Знак
|
Направление процесса в потенциальном поле |
|
1 |
разноименные эл. заряды |
электростатическое |
притяжение |
|
|
|
- |
+ |
по градиенту |
|
отталкивание |
|
|
|
+ |
- |
против градиента |
|||
|
2 |
одноименные эл. заряды |
электростатическое |
притяжение |
|
|
|
+ |
- |
против градиента |
|
отталкивание |
|
|
|
- |
+ |
по градиенту |
|||
|
3 |
элементарные массы |
гравитационное |
притяжение |
|
|
|
- |
+ |
по градиенту |
|
отталкивание |
|
|
|
+ |
- |
против градиента |
|||
|
4 |
деформация пружины |
поле упругих сил |
сжатие |
|
|
|
+ |
- |
против градиента |
|
растяжение |
|
|
|
+ |
- |
против градиента |
|||
|
5 |
фотоэффект |
электростатическое |
отталкивание |
|
|
|
- |
+ |
по градиенту |
Поэтому, на основе анализа первого начала термодинамики было установлено:
1. Все явления и процессы в природе и в мире, включая человека, технику, экономику и экологию, идут только в двух энергетических направлениях. Или - по градиенту силового поля, с минимальной затратой энергии, или - против градиента, с максимальной затратой энергии. Первое направление соответствует понятию энтропия, а второе - понятию негэнтропия (отрицательная энтропия). В динамике процессов оба явления взаимосвязаны, и дополняют друг друга.
2. В системах, в которых взаимодействие идет по градиенту потенциала (положительная работа) результирующая потенциальная энергия, как и приведенная масса, находятся по принципу сложения обратных значений соответствующих величин подсистем. Это – корпускулярный процесс, теоретической концепцией которого может являться энтропия.
3. В системах, в которых взаимодействие идет против градиента потенциала (отрицательная работа) выполняется алгебраическое сложение их масс и также соответствующих энергий подсистем. Это – волновой процесс, теоретической концепцией которого может являться негэнтропия.
4. Резонансное стационарное состояние систем выполняется при условии равенства степеней их корпускулярных и волновых взаимодействий. В термодинамике открытых систем продукция энтропии в стационарном состоянии полностью компенсируется потоком негэнтропии.
3. Энтропийные составляющие атома
Изначально свободный атом представляет собой систему двух противоположных начал: электроны – ядро атома. Положительный заряд ядра создает поле центральной силы, в котором расположено электронное облако, и совершается движение электронов. В кинематике любого вращательного движения действуют две составляющие ускорения: центростремительное – направленное к центру по градиенту поля – это корпускулярная составляющая, теоретической концепцией которой является энтропия. И есть линейное ускорение, направленное по касательной от атома, то есть против градиента поля, концепцией которого является негэнтропия. Это волновая часть процесса. Условия энтропийно-равновесного состояния между этими составляющими определяют стабилизацию всей структуры в соответствии с уравнением Планка для атомных центров:
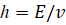 ,
,
где 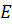 –орбитальная энергия, в стационарном состоянии – величина постоянная, процесс идет по градиенту поля (энтропия),
–орбитальная энергия, в стационарном состоянии – величина постоянная, процесс идет по градиенту поля (энтропия), 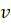 – частота электромагнитной волны (негэнтропия),
– частота электромагнитной волны (негэнтропия), 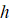 – постоянная Планка. И при упруго-гармонических колебаниях тоже есть две составляющие кинетической и потенциальной энергии. Их соотношение дает:
– постоянная Планка. И при упруго-гармонических колебаниях тоже есть две составляющие кинетической и потенциальной энергии. Их соотношение дает:
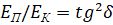 ,
,
где 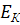 – кинетическая энергия,
– кинетическая энергия, 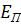 – потенциальная энергия, а
– потенциальная энергия, а 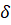 – угловая характеристика колебаний.
– угловая характеристика колебаний.
При условии равенства 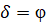 , система получает энтропийное равновесное состояние (где
, система получает энтропийное равновесное состояние (где 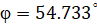 – энтропийный геодезический угол). Именно под данным углом тутовый шелкопряд наматывает шелковую нить на основу.
– энтропийный геодезический угол). Именно под данным углом тутовый шелкопряд наматывает шелковую нить на основу.
Аналогичные явления присутствуют и в макропроцессах, например, в технике, при изготовлении летательных космических аппаратов. В этом примере используются данные из [2]. При изготовлении космических аппаратов намотка высокопрочной нити на корпус проводится под геодезическим углом, в соответствии с энтропийными соотношениями:
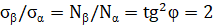
где: 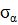 – осевое,
– осевое, 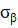 – окружное напряжения заменяются пропорциональной им величиной
– окружное напряжения заменяются пропорциональной им величиной 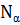 – осевое «усилие» и
– осевое «усилие» и 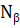 – окружное «усилие».
– окружное «усилие».
Это условие позволяет получать равнонапряженную систему нитей с минимальной массой изделия.
Между самими противоположными составляющими энтропии тип взаимодействия зависит от знака их электрического заряда. Если обе составляющие одноименного электрического заряда, то в этом случае выполняется принцип алгебраического сложения их составляющих. Например, максимальная энергия при упруго-колебательных процессах равна сумме кинетической и потенциальной энергии, и всегда является постоянной величиной.
Если обе составляющие энтропии электронейтральны, или у них величины энергетических параметров мало отличаются, то в этом случае также выполняется принцип алгебраического сложения. Если обе составляющие противоположного электрического заряда, то сумма этих составляющих находится по принципу сложения их обратных величин. Так происходит и в системе «электрон-ядро», и полученная таким методом суммарная энергия уменьшается, но является достаточной и наиболее эффективной в структурных взаимодействиях.
Функция Гамильтона равна сумме кинетической и потенциальной энергии. То есть – это полная механическая энергия системы. Но Гамильтониан выполняется только для систем с однородной функцией второй степени.
Например - две частицы вместе совершают свободное поступательное движение. У них и массы и энергии суммируются алгебраически. Но если эти же частицы двигаются в поле центральных сил с общей энергией, то такие частицы уже не однородные – у них и массы и энергии суммируются по принципу сложения обратных величин. Так, в сложной многокомпонентной системе при внешнем технологическом воздействии – общая энергия системы уменьшается.
Другой пример: уравнение Лагранжа для относительного движения изолированной системы двух взаимодействующих материальных точек с массами m1 и m2, которое в координате х имеет вид:
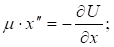
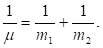
Здесь U – взаимная потенциальная энергия материальных точек; 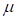 – приведенная масса.
– приведенная масса.
При этом х″ = a (характеристика ускорения системы). Для элементарных участков взаимодействий ?х можно принять:
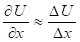 То есть:
То есть: 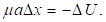 И тогда:
И тогда:
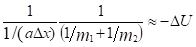
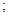
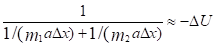
Или: 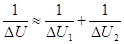
где ?U1 и ?U2 – потенциальные энергии материальных точек на элементарном участке взаимодействий, ?U – результирующая (взаимная) потенциальная энергия этих взаимодействий.
4. Пространственно-энергетический параметр (Р-параметр)
На основе установленных принципов энтропии, максимальная энергия атома может быть рассчитана по принципу сложения обратных величин исходных энергетических составляющих, согласно уравнениям:
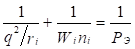 или
или 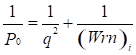 ;
; 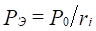 (1),(2),(3)
(1),(2),(3)
здесь: Wi – орбитальная энергия электронов [3]; ri– орбитальный радиус i–ой орбитали [4]; q=Z*/n* - по [5], ni – число электронов данной орбитали, Z*и n* - эффективный заряд ядра и эффективное главное квантовое число, r – размерные характеристики связи.
Величина РО названа пространственно-энергетическим параметром (ПЭП), а величина РЭ – эффективным Р–параметром (эффективный ПЭП). Эффективный ПЭП имеет физический смысл максимальной энергии атома, и измеряется в единицах энергии, например - в электрон-вольтах (эВ).
Значения Р0-параметра являются табулированными постоянными величинами для электронов данной орбитали атома.
Для размерности ПЭП можно записать:
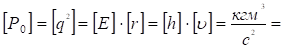 Дж×м,
Дж×м,
где [E], [h] и [υ] – размерности энергии, постоянной Планка и скорости. Таким образом, такой Р-параметр соответствует процессам, идущим по градиенту потенциала.
Введение Р-параметра следует рассматривать как последующее развитие квазиклассических представлений с использованием квантовомеханических данных по строению атома для получения критериев энергетических условий фазообразования. При этом для систем одноименно-заряженных (например, – орбитали в данном атоме), или однородных систем - сохраняется принцип алгебраического сложения таких параметров:
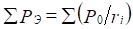 ;
; 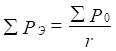 (4),(5)
(4),(5)
или: 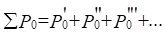 ;
; 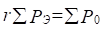 (6),(7)
(6),(7)
Здесь Р-параметры суммируются по всем валентным орбиталям атома.
Для вычисления значения РЭ-параметра на данном расстоянии от ядра в зависимости от вида связи вместо 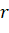 может использоваться или атомный радиус (R) или ионный радиус (
может использоваться или атомный радиус (R) или ионный радиус (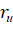 ).
).
Далее даны примеры применения такой методики в материаловедении.
5. Растворимость компонентов в металлической системе Co-W-Ni-Cr-Fe[6]
Используя в качестве орбитальной энергии электронов величину энергии их связи [3] по уравнению (1) были рассчитаны Р-параметры валентных орбиталей элементов, входящих в систему Co-W-Ni-Cr-Fe (табл.2). При этом их эффективные Рэ-параметры определялись по уравнению:
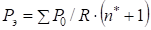 , (8)
, (8)
где R - атомный радиус по Белову-Бокию.
Здесь и далее часть таблиц дается в значительном сокращении в качестве иллюстрации.
Таблица 2. Р-параметры атомов элементов сплава
|
Атомы |
Валентные электроны |
W, эВ |
ri, Å |
q2, эВА |
∑Po, эВА |
R, Å |
Ро/R, эВ |
Рэ=∑Po/ R(n*+1), эВ |
|
С |
2Р1 |
11.792 |
0.596 |
35.395 |
5.868 |
0.77 |
7.6208 |
2.5403 |
|
2Р2 |
11.792 |
0.596 |
35.395 |
10.06 |
13.066 |
4.3554 |
||
|
2S1 |
19.201 |
0.620 |
37.240 |
9.021 |
11.715 |
3.9052 |
||
|
2S2 |
19.201 |
0.620 |
37.240 |
14.524 |
18.862 |
6.2874 |
||
|
2Р2+2S2 |
|
|
|
24.585 |
31,929 |
10,643 |
||
|
* для Кr=12 |
|
|
|
|
0.86* |
28.587 |
9.5291 |
|
|
W |
6S1 |
6.1184 |
1.36 |
38.838 |
6.8528 |
1.4 |
4.8949 |
0.9413 |
|
6S2 |
|
|
|
11.650 |
8.3214 |
1.6003 |
||
|
5d3 |
12.093 |
0.746 |
161.43 |
23.178 |
16.556 |
3.1838 |
||
|
5d4 |
|
|
|
29.493 |
21.066 |
4.0512 |
||
|
6S2+5d3 |
|
|
|
34.828 |
24.877 |
4.7841 |
||
|
6S2+5d4 |
|
|
|
41.143 |
29.388 |
5.6515 |
Количественным критерием растворимости системы является относительная разность Р-параметров атомов элементов, составляющих сплав:
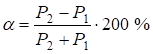 , (9)
, (9)
где Р1 – Рэ-параметр атомов первого компонента или структурной составляющей; Р2 – Рэ-параметр атомов второго компонента или структурной составляющей.
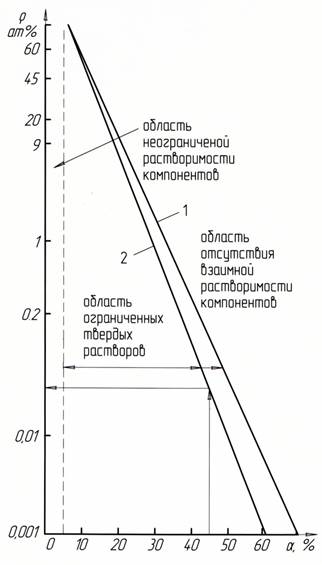
Рис.1. Номограмма к расчету растворимости компонентов ρ (в логарифмической шкале) в зависимости от коэффициента α: 1 – для металлических систем; 2 – для карбидов
Обработка результатов расчетов по данной методике позволила получить единую номограмму зависимости взаимной растворимости компонентов металлических систем от коэффициента α (рис.1, зависимость 1). На рисунке 1 дана такая номограмма в логарифмическом варианте для линейной зависимости. Так для бинарных металлических систем непрерывный ряд твердых растворов имеет место при α<4-6%, отсутствие растворимости – при α>50-60%, между ними – ограниченная растворимость.
Таблица 3. Оценка взаимной растворимости бинарных компонентов в сплаве
|
Атом и его валентность |
Направление растворимости |
Рэ , эВ |
РТ , эВ |
α , % |
ρ , ат% |
|
|
расчет |
эксперимент |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
W (5) |
W→Cr |
4.7841 5.5406 |
3.9163 |
34.45 |
2.1 |
Т Ограниченная растворимость |
|
Cr (6) |
||||||
|
W (6) |
W→Cr |
5.6515 |
4.6263 |
18.1 |
17.5 |
|
|
Cr (6) |
5.5406 |
|||||
|
Cr (6) |
Cr → W |
5.5406 |
6.3629 |
11.8 |
42-45 |
|
|
W (6) |
5.6515 |
|||||
|
Cr (3) |
Cr → W |
2.8762 |
3.3030 |
12.13 |
41 |
О.Т.Р.
Т |
|
W (4) |
3.7296 |
|||||
|
Cr (3) |
W→Cr |
2.8762 |
3.0531 |
5.97 |
100 |
|
|
W (4) |
3.7296 |
|||||
|
Cr (2) |
W→Cr |
1.7650 |
1.7313 |
1.93 |
100 |
|
|
W (2) |
1.6003 |
|||||
|
Co (2) |
2.1629 |
|||||
Зависимость α от температуры плавления компонентов сплава учитывалась по уравнениям:
- для компонента с большей температурой плавления:
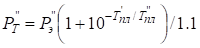 ; (10)
; (10)
- для компонента с меньшей температурой плавления:
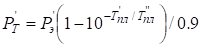 , (11)
, (11)
где Рт – приведенное «температурное» значение Р-параметра; T” – более высокая температура плавления одного компонента; T' – более низкая температура плавления другого компонента.
С учетом подстановки (10 и 11) в (9) получим:
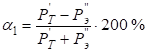 , (12)
, (12)
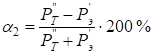 . (13)
. (13)
Используя значения рассчитанных Р-параметров (табл.2), по уравнениям (10) и (11) были определены Рт – параметры, для рассматриваемой металлической системы Co-W-Ni-Cr-Fe, приведенные к температуре другого компонента. При этом расчеты проводили в предположении парного взаимодействия атомов элементов М’-М” для всех возможных их вариантов сочетаний. Далее по уравнениям (12) и (13) находились коэффициенты структурного взаимодействия α. Результаты расчетов приведены в таблице 3.
Таблица 4. Р-параметры систем с полной растворимостью компонентов (ρmax=100%)
|
Система компонентов (их валентность) |
|
|
|
|
|
Т |
||||
|
Со-Ni-Fe (2-2-2) |
0.721 |
0.727 |
0.716 |
2.164 |
|
Со-Ni-Fe (3-3-3) |
0.952 |
0.966 |
0.938 |
2.856 |
|
Т |
||||
|
W-Cr (2-2) |
0.80015 |
0.8825 |
- |
1.6827 |
|
W-Cr (4-3) |
1.8648 |
1.4381 |
- |
3.3029 |
|
W-Cr (4-3)(система с широкой растворимостью) |
2.2005 |
1.1792 |
- |
3.3797 |
При всех вычислениях основными валентно-активными орбиталями считались те из них, которые отвечают наиболее устойчивой степени окисления: для железа, никеля и кобальта – (+2, +3); для хрома – (+3, +6); для вольфрама – (+6, +5, +4, +2).
Таблица 5. Растворимость компонентов системы (W-Cr)-(Co-Ni-Fe)
|
Система компонентов и направление растворимости |
|
|
|
РТ, эВ |
α, % |
ρ, ат.% |
|
При температурах процесса менее 1800оК (Т’пл/Т”пл=1765/3680) |
||||||
|
(Co-Ni-Fe)
|
0,8096 |
4,5759 |
5,3806 |
3,4558 |
43,6 |
0,44 |
|
(W-Cr) |
0,8096 |
4,5759 |
5,3806 |
4,002 |
33,4 |
2,3 |
|
При температурах процесса более 2133оК (Т’пл/Т”пл=1765/3680) |
||||||
|
(W-Cr) |
3,3029 |
2,1634 |
- |
2,4560 |
12,7 |
39-40 |
|
(Co-Ni-Fe)
|
3,3029 |
2,8565 |
- |
3,4558 |
4,52 |
100 |
|
(W-Cr) |
3,3745 |
2,8565 |
- |
2,5093 |
12,9 |
39-40 |
|
(Co-Ni-Fe)
|
3,3745 |
2,8565 |
- |
3,4558 |
2,37 |
100 |
По данным таблицы 3 установлено, что элементы 8-ой группы Fe, Co и Ni образуют между собой непрерывные твердые растворы. Для них взаимодействие наиболее валентно-активных орбиталей соответствуют меньшим внешним энергетическим затратам при более низкой температуре. Элементы Wи Cr имеют ограниченную растворимость, как между собой, так и в кобальтовой матрице, в железе и никеле. Однако в системе W-Cr для состояния W(4)-Cr(3) и W(2)-Cr(2) при температуре выше температуры плавления хрома расчеты показывают существование непрерывных твердых растворов. Если учесть, что температура сварочной ванны расплава составляет 1923-2123оК, а температура анодного пятна электрической дуги достигает 2573оК [7], то можно предположить, что все элементы сплава в расплавленном состоянии образуют между собой твердый раствор. При последующем понижении температуры расплава (ниже температуры плавления хрома 2133оК) в процессе кристаллизации сплава атомы элементов вольфрама и хрома для состояний W(5)-Cr(6) и W(6)-Cr(6) образуют между собой ограниченные твердые растворы. Эти результаты имеют удовлетворительное совпадение с экспериментальными данными работ [8,9]. Поэтому, с учетом ранее установленного принципа алгебраического сложения Р-параметров однородных систем, сплав при более низких температурах был рассмотрен как система, состоящая из компонентов (W-Cr) и (Co-Ni-Fe), для которой были определены РС-параметр, РТ-параметр и α, приведенные в табл. 4 и 5.
Анализ полученных данных показал, что при высоких температурах (более 21330К) в направлении (W-Cr)  (Co-Ni-Fe) идет образование непрерывных твердых растворов (α<4,52%), что подтвердило выдвинутое выше предположение. Обратное направление процесса растворения дает сужение этой области до α <12,9% и по номограмме (рис.1, зависимость 1) растворимость составит ρ=39-40 ат%. При температурах ниже температуры плавления хрома их растворение определяется значениями α1=41,1% и α2=44,2% (табл. 5) и, согласно диаграмме (рис.1, зависимость 1), область твердых растворов будет значительно ограничена.
(Co-Ni-Fe) идет образование непрерывных твердых растворов (α<4,52%), что подтвердило выдвинутое выше предположение. Обратное направление процесса растворения дает сужение этой области до α <12,9% и по номограмме (рис.1, зависимость 1) растворимость составит ρ=39-40 ат%. При температурах ниже температуры плавления хрома их растворение определяется значениями α1=41,1% и α2=44,2% (табл. 5) и, согласно диаграмме (рис.1, зависимость 1), область твердых растворов будет значительно ограничена.
6. Оценка энергии активации процессов диффузии. [10]
Поскольку атомы твердых тел состоят из ионов и относительно свободных электронов, движущихся в определенных пространственных зонах, можно предположить взаимосвязь между энергией активации диффузии и электронным взаимодействием атомов в кристаллической решетке тела. Исходя из этого, энергию активации диффузии (Еа) рассмотрим как энергию межатомного (парного) взаимодействия атомов А окружающей среды и диффундирующего в ней атома компонента В. Если энергия поступательного движения атома В больше энергии межатомного взаимодействия с атомами А, то он диффундирует за пределы окружающих его атомов А. Если же атом В будет иметь энергию движения меньше, чем энергия его взаимодействия с атомами А, то он не сможет мигрировать за пределы этих атомов. В этом случае не будет происходить обменного процесса между атомами А и В, то есть диффузия невозможна. Наконец, если энергии атомов равны, то создаются условия для образования пары: междоузельный атом – вакансия. Таким образом, оценка энергии активации (в данном случае диффузии) сводится к определению реальной энергии парного или иного вида взаимодействия диффундирующего атома и атомов окружающей его среды.
С учетом исходных принципов энтропии, результирующую величину эффективной энергии парного взаимодействия атомов А и В, тождественную энергии активации процесса диффузии, получим в виде суммы обратных величин Р-параметров:
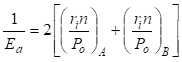 , (14)
, (14)
где Еа – энергия активации процесса диффузии атома Вв среде атомов А; n - число всех валентных электронов, или число наиболее удаленных от ядра валентных электронов конкретного атома.
При диффузии атома Вв однородной по составу и подобной ему среде с атомами В значение Еаприобретает смысл энергии активации самодиффузии атома В. Исходя из (5) она определится как:
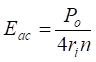 , (15)
, (15)
Сопоставление результатов расчетов с экспериментальными данными показало их удовлетворительное совпадение (табл. 6). Погрешность составила не более 5 ат%. Таким образом, пространственно-энергетический параметр является своеобразным «паспортом» атома и всего металла или сплава в целом, по которому расчетным путем можно оценить результаты его взаимодействия с другими металлами, сплавами, или химическими элементами.
Таблица 6. Энергия активации диффузии атомов в металлических системах
|
Растворитель |
Диффундирующий элемент |
Еас,эВ |
|||||
|
Атомы |
P0, эBÅ n |
rИ, Å |
Атомы |
P0, эBÅ n |
rИ, Å |
Расчет по (6-7) |
Литературные данные |
|
g-Fe (4S23d1) |
29,026 3 |
0,67 |
g-Fe (4S2) |
18,462 2 |
0,80 |
3,207 |
2,8-3,2 |
|
самодиффузия |
|||||||
|
Cr (4S13d2) |
25,835 3 |
0,64 |
3,483 |
3,468 |
|||
|
C (2P3) |
32,458 3 |
2,60 |
1,615 |
1,586 |
|||
|
Mn (4S2) |
18,025 2 |
0,91 |
2,937 |
2,71-2,861 |
|||
|
g-Fe (4S2) |
18,462 |
0,80 |
Mn (4S2) |
18,025 2 |
0,91 |
2,665 |
2,419 |
|
Ni (4S2) |
18,838 2 |
0,74 |
3,026 |
2,905 |
|||
|
Mo (5S14d1) |
17,475 2 |
0,915 |
2,613 |
2,557 |
|||
|
W (6S15d1) |
20,689 2 |
0,98 |
2,792 |
2,709 |
|||
Выводы
1. Максимальная и эффективная энергии атомной структуры равны сумме их энтропийных энергетических составляющих.
2. Данное суммирование выполняется для систем в равновесном энтропийном состоянии, и по специальным правилам.
3. Получен пространственно-энергетический параметр, численно равный наиболее эффективной энергии в структурных взаимодействиях.
4. Разработан расчетно-аналитический метод оценки растворимости и фазообразования для сложных многокомпонентных металлических систем. Результаты проведенных расчетов удовлетворительно согласуются с экспериментальными данными.
5. Приведена, основанная на энтропийных принципах, методика расчета энергии активации самодиффузии и объемной диффузии атомов в твердых телах.

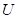
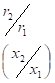
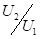
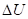
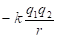
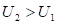
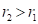
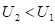
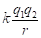
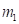 и
и 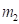
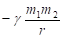
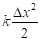
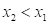

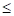 1768оК
1768оК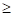 2233оК
2233оК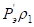 , эВ
, эВ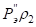 , эВ
, эВ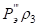 , эВ
, эВ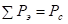 , эВ
, эВ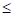 2133оК
2133оК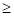 2133оК
2133оК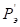 , эВ
, эВ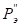 , эВ
, эВ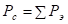 , эВ
, эВ