Введение
В работе рассматривается возможность нахождения произведения двух сомножителей, состоящих из произвольного количества произвольных цифр, используя предложенные ранее способы умножения [1 – 4], где первый сомножитель состоял только из произвольных, но одинаковых цифр.
Цель работы
Предложить еще один способ умножения двух сомножителей, состоящих из произвольного количества произвольных цифр.
Будем рассматривать первый сомножитель как состоящий из блоков различных, но однородных цифр с произвольным их количеством в каждом блоке, а второй сомножитель – произвольный.
Результатом произведения блоков на второй сомножитель записываем также в виде блоков в порядке их расположения в первом сомножителе слева направо. Затем блоки полученных произведений соединяются в соответствие с предложенным далее правилом и записывается окончательный ответ.
Способы нахождения произведения каждого отдельного блока могут быть разными в зависимости от количества цифр (периодических) в блоке (одна, две, три и т.д.) в соответствие с изложенными ранее в работе [1, 2, 4]. Чаще всего применяются методы «скобок-1» и «скобок-2». В случае периодических девяток и единиц можно сразу записать формализованный ответ. Можно использовать и другие способы.
Рассмотрим различные примеры.
Пусть первый сомножитель состоит из трех блоков, в каждом из которых содержатся по 3 различных периодических цифры, а второй сомножитель – произвольное двузначное число. Также рассмотрим различные вариации количества цифр в сомножителях.
Примеры:
Найти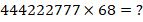 
Решение.
Первый сомножитель состоит из трех блоков различных однорядных цифр:
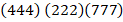
Найдем по отдельности произведение каждого из блоков на 68.
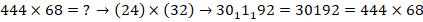
Здесь применили метод «скобок-2» – метод суммирования нечетного количества цифр [2]:
1, 3, 431, справа налево,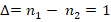 
.
Аналогично для второго и третьего блоков:
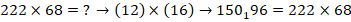
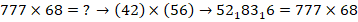
Замечание: индексы везде указывают количество десятков, прибавляемых к единицам соседнего левого разряда.
Далее записываем ответы произведений в порядке расположения блоков первого сомножителя. Выделили их в скобках:
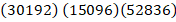
Для получения окончательного ответа произведения сомножителей сформулируем правило перехода между соседними блоками (скобками) ответа.
В последней скобке (третьем блоке ответа) остаются неизменными и переходят в окончательный ответ последние цифры в количестве, равном их количеству в последнем блоке первого сомножителя (777). Неизменные части в каждом подобном случае будем выделять рамкой. В третьем (последнем) блоке это 836. Оставшиеся цифры блока суммируются с последними цифрами соседнего предыдущего (левого) блока ответа.
Далее со второй скобкой поступаем аналогично. Ее последние цифры после суммирования в количестве равном их количеству во втором блоке первого сомножителя входят в окончательный результат ответа. Аналогичным образом, оставшиеся цифры первого блока ответа и результат полностью записываются в начале окончательного ответа исходного произведения. За ними идут неизменные цифры второго и третьего блоков ответа.
Аналогично поступают во всех далее рассматриваемых случаях.
Итак, неизменными (входящими в окончательный ответ) цифрами последних трех случаев остаются 836, а 52 суммируются с числом второй скобки.
Т.е.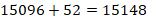 
.
Аналогично, т.к. во втором блоке первого сомножителя тоже три цифры, здесь неизменным остается число 148. Записывается слева от неизменного числа третьего блока.
Далее переходим к первому блоку ответа аналогично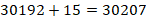 
.
Это число полностью входит в окончательный ответ, располагаясь в начале его.
Получим: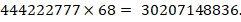 
Замечание: во всех случаях блочного умножения запись окончательного ответа производится справа налево.
2) Найти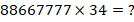 
Решение.
Выделим скобками:
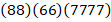
Найдем произведения каждого блока на 34, применяя метод «скобок-2».
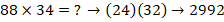
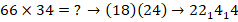
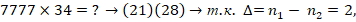
где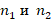 
соответственно количество цифр первого и второго сомножителей, тогда в середину ответа включается двукратное суммирование всех цифр обеих скобок
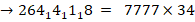
Запишем результат произведений в виде блоков ответа, согласно их расположению в первом сомножителе.
Получим: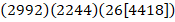 
Далее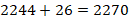 
, 
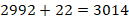
Ответ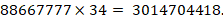 
Во всех случаях количество цифр в ответе равно их сумме в обоих сомножителях, кроме случаев, когда произведение первых цифр сомножителей – одночлены. В этом случае для формализации ответа впереди можно добавить 0. [1]
3) Найти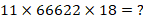 
Решение.
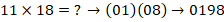
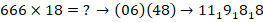
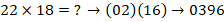
Записываем блоки ответов
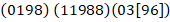
Далее, согласно правилу: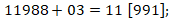
.
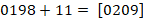Ответ: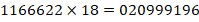 
4) Найти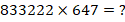 
Решение.
Для блоков одночлена (8) и двучлена (33) воспользуемся методом «скобок-1» с пошаговым суммированием цифр справа налево, а для третьего блока (222) первого сомножителя – методом суммирования «скобок-2» как наиболее удобным в этом случае.
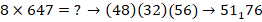
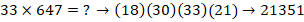
Пояснение: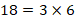 
; 
;
; 
.
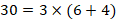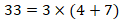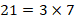Т.е. сначала периодическое число умножается на первую цифру второго сомножителя, затем пошагово на сумму двух рядом стоящих цифр второго сомножителя, заканчивая умножением периодического числа на последнюю цифру. Все произведения записываются последовательно в виде скобок.
В случае, если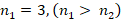 
, можно воспользоваться тем, что периодическое число умножается последовательно сначала на первую цифру второго сомножителя, затем на сумму второго, двух первых его цифр, затем на сумму трех и далее суммируем по три цифры с каждым шагом смещаясь на одну цифру к концу второго сомножителя, затем сумму последовательно уменьшаем до одной (последней) цифры. Результаты произведения записываем в виде скобок в соответствие с порядком умножения и суммируя пошагово справа налево записываем ответ. Алгоритм аналогичен для 
.
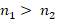Или
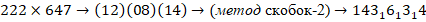
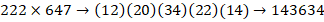
Составим блоки ответа
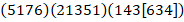
Затем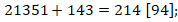 
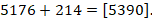
Ответ: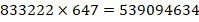 
.
5) Найти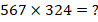 
Решение.
Здесь (5), (6), (7) периодические цифры – одночлены каждого блока первого сомножителя.
Тогда имеем
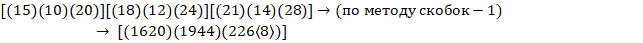
Далее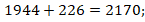 
.
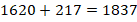Итак, ответ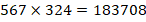 
6) Найти 732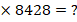
Решение. Блоки перового сомножителя (7)(3)(2)
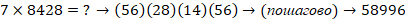
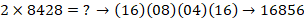
Блоки ответа:
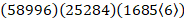
Далее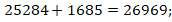 
.
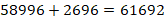Ответ: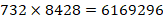 
.
Заключение.
Метод представляет интерес как еще один удобный способ нахождения произведения двух сомножителей, состоящих из разного количества произвольных цифр, особенно, когда первый сомножитель включает блоки с несколькими методическими цифрами.