Scientific journal

Scientific Review. Fundamental and Applied Research

Введение. В настоящее время наблюдаются глобальные климатические изменения, связанные с повышением среднегодовой температуры воздуха на планете (так называемое глобальное потепление). Прогнозируется, что в ближайшем будущем эти изменения будут только усиливаться и приведут к существенным последствиям для всей климатической системы. Особо уязвимым климатическим элементом природной среды является вечная мерзлота, которая занимает большую часть Северного полушария Земли [1].

Многолетнемерзлые грунты, часто называемые вечной мерзлотой, встречаются более чем на 60% территории России [2]. На этой территории десятками лет строилась нужная инфраструктура, которая учитывает все особенности подстилающей поверхности. Таяние вечной мерзлоты может значительно усложнить экономическое положение соответствующих регионов [3].

В настоящей работе рассматривается модель сезонного таяния многолетнемерзлых грунтов, со слоями, имеющими различные характеристики. Это позволяет учесть и описать особенности сезонного изменения температурного режима грунта, где могут возникнуть слои промерзшей почвы и воды.

Целью исследования является реализация численного решения задачи теплопроводности конечно-разностным методом с переменными характеристиками, а также изучение зависимостей температуры грунта от различных параметров.

Материалы и методы исследования. Для анализа влияния повышения среднегодовой температуры воздуха на структуру промерзшего грунта будет использована глобальная климатическая модель [3, 4] и сценарии изменения концентрации углекислого газа в атмосфере [5].

Для Пятого доклада МГЭИК [5] научные эксперты выбрали набор из четырех новых сценариев, именуемых репрезентативными траекториями концентраций (РТК). Они задают приблизительные суммарные величины радиационного форсинга (воздействия) в 2100 г. по сравнению с 1750г.: 2.6 Вт/м2 для сценария РТК2.6; 4.5 Вт/м2 для сценария РТК4.5; 6.0 Вт/м2 для сценария РТК6.0 и 8.5 Вт/м2 для сценария РТК8.5.

Эти четыре РТК имеют один сценарий сокращения выбросов, который предполагает весьма низкий уровень воздействия (РТК2.6); два сценария стабилизации (РТК4.5 и РТК6.0) и один сценарий с достаточно высокими уровнями выбросов парниковых газов (РТК8.5) [4]. Таким образом, эти сценарии могут представлять результаты целого ряда направлений политических мер в области климата в XXI веке. Согласно РТК6.0 и РТК8.5, радиационное воздействие продолжает расти вплоть до 2100 г., в РТК2.6 оно достигает максимума и затем снижается; и в РТК4.5 оно стабилизируется к 2100 г. Каждый сценарий дает наборы данных с высоким пространственным разрешением по изменениям в землепользовании и выбросам загрязняющих воздух веществ по секторам экономики, а также определяет годовые концентрации парниковых газов и антропогенные выбросы до 2100 г [5].

Модель общей циркуляции атмосферы (ОЦА) - это комплекс программ, который описывает многие глобальные физические процессы в атмосфере. Имеются два основных блока программы: блок динамики модели ОЦА, в котором вычисляются течения в атмосфере, описываемые примитивными уравнениями, и блок физики, в котором определяются солнечные и тепловые радиационные потоки, рассматриваются адиабатические, влажные и конвекционные процессы. Результаты, полученные в этом блоке, используются в блоке динамики для вычисления течений и термодинамических характеристик атмосферы [3]. Модель ОЦА дополняется моделью мирового океана [4, 6, 7].

По совместной глобальной модели проведены расчеты прогнозирования климата до 2100 г. с использованием сценариев роста СО2 РТК8.5 и РТК4.5 (рис. 1, 2), предложенных МГЭИК. Некоторые результаты сведены в табл. 1 [3,8].

Таблица 1. Результаты расчетов по сценариям РТК8.5 и РТК4.5. Изменения климатических характеристик по сравнению с 2010 г.

В настоящей работе рассматривается модель сезонного таяния многолетнемерзлых грунтов, со слоями, имеющими различные физические характеристики. Это позволяет учесть и описать особенности сезонного изменения температурного режима грунта, где могут возникнуть слои промерзшей почвы и воды.

Исследование ведется на основе численного решения уравнения теплопроводности с плотностью, коэффициентами теплопроводности и теплоемкости грунта, зависящими от агрегатного состояния влаги грунта. Граничные условия на поверхности определяются заданием ее температуры в соответствии с сезонным ходом или постоянной величиной. На нижней границе вертикального слоя грунта задается либо постоянная температура, либо условие отсутствие потока тепла. Учитывается возможность фазового перехода внутри слоя с вычисляемой подвижной границей. Эта граница определяется температурой замерзания влаги почвы, а потоки тепла на границе формируются с учетом скрытой теплоты замерзания (таяния). Вместо скачкообразного изменения характеристик почвы на указанной границе предлагается резкое, но непрерывное изменение этих характеристик. Изменение во времени координаты точки фазового перехода определяется на каждом шаге по времени с учетом скрытой теплоты фазового перехода, суммируется до достижения значения величины одного шага по координате, после чего происходит соответствующее изменение координаты фазового перехода. Это позволяет вести сквозной счет уравнения теплопроводности.

Для численного решения задачи используется конечно-разностный метод с равномерной по глубине грунта сетке. Значение температуры грунта и объемная теплоемкость задаются в центрах ячеек, а значение коэффициента теплопроводности - на границах ячеек, таким образом достигается консервативность (сохранение энергии) для конечно-разностной задачи. Расчеты проведены для различных глубин грунта от 10 м до 30 м и различных температур на нижней границе слоя грунта от +5оС до -5оС. Выход на установившийся режим происходит примерно за 10 лет.

Предлагаемый конечно – разностный метод решения, имеет преимущество в том, что он допускает произвольную нелинейную зависимость параметров модели от температуры и глубины. Модель предполагается использовать как отдельный блок в глобальной модели климата при прогнозах его изменения [3].

Результаты исследования и их обсуждение. На рис. 1 приведены результаты расчетов изменения во времени средней температуры грунта для варианта нулевого потока тепла на глубине 10 м и сезонного хода температуры на поверхности. Выход на установившийся режим происходит примерно за 10 лет. На рис 1б приведены результаты расчетов распределения температуры по глубине в моменты времени от 1 года до 9 лет при постоянной температуре на поверхности, равной -5оС и нулевому потоку тепла на нижней границе. В обоих случаях начальная температура грунта постоянная и равна 20 оС.

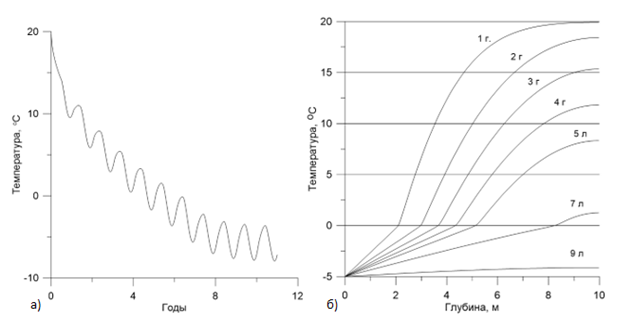
Рисунок 1 – выход на стационарный режим

Графики распределения температуры грунта по глубине для четырех сезонов для 2010 года с фиксированной температурой -5оС и +5оС на нижней границе 10 м приведены на рис. 2.

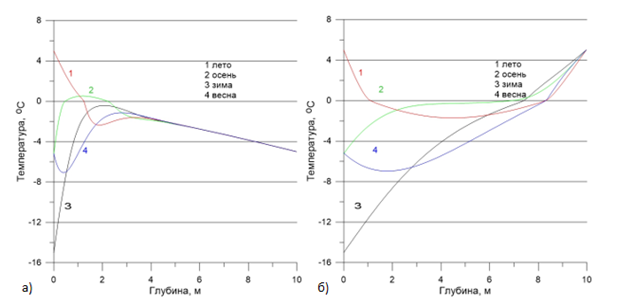
Рисунок 2 –Зависимость температуры грунта от глубины для четырех сезонов для 2010 года и с фиксированной температурой на нижней границе 10 м: а) -5оС и б) +5оС

Из рис. 2а следует, что распределение температуры грунта не зависит от сезона на глубинах, больших 4 м, это связано с коротким промежутком положительной температуры воздуха, слой грунта не успевает прогреваться и находится в стационарном состоянии. На рис. 2б температура меняется вплоть до точки с фиксированной температурой на глубине 10 м, это демонстрирует сильную зависимость характера мерзлого грунта от граничных условий на глубине.

Постоянная температура на нижней границе слоя грунта может использоваться для анализа зон вечной мерзлоты с промерзанием на большие глубины, чтобы упростить расчеты и не создавать сетку на всю глубину грунта, а использовать глубину до 6 м и фиксировать температуру при значении -4.5 оС. Постоянная положительная температура на нижней границе слоя грунта может оказать влияние температуры земли на характер промерзания почвы. На рис. 2б видно, что температура на нижней границе влияет на промерзание и уже не наблюдается вечной мерзлоты, остается сезонная.

На рис. 3 приведена зависимость температуры грунта от глубины для четырех сезонов для 2010 года для варианта расчета при нулевом потоке тепла на нижней границе 10 м. Отметим переменную температуру на нижней границе для всех сезонов.

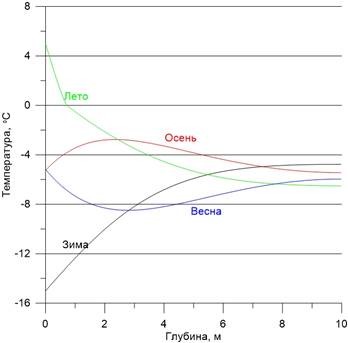
Рисунок 3 - Зависимость температуры грунта от глубины для четырех сезонов для 2010 года при нулевом потоке тепла на нижней границе 10 м

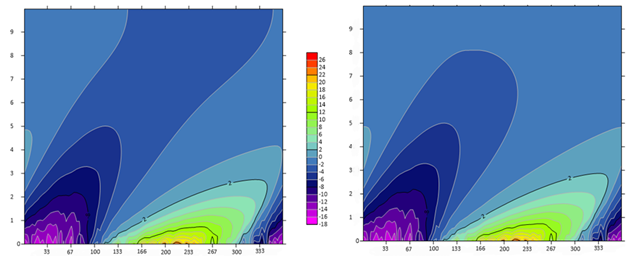
а) б)

Рисунок 4 – Изолинии распределения температуры грунта в зависимости от дня года (горизонтальная ось) и глубины (вертикальная ось) с фиксированной температурой на нижней границе 10 м (а) и при нулевом потоке тепла на нижней границе 10 м (б)

Рис. 4 показывает динамику изменения температуры грунта по дням года, можно заметить, что грунт прогревается не сразу, а с накопительным эффектом и тепло полученное грунтом летом может влиять на распределение вплоть до зимы. Поэтому при анализе вечной мерзлоты важно учитывать не только связь со среднегодовой температурой, но еще учитывать и длительность теплого периода. Если среднегодовая температура будет низкой, но при этом продолжительное время будет поддерживаться положительная температура на поверхности, то грунт будет успевать прогреваться и не успевать промерзать, что приводит к отсутствию вечной мерзлоты в регионах, где среднегодовая температура отрицательна или к сезонной мерзлоте в регионах с низкой температурой зимой.

При увеличении средней температуры воздуха на 2оС - 3оС конечное распределение температуры грунта будет зависеть от глубины грунта, а также начальной температуры. При большой глубине промерзания изменения будут затрагивать лишь первые 30 м, для оттаивания более глубоких участков необходимо более длительное воздействие или существенное изменение температуры воздуха.

Проанализирована также зависимость накопительной погрешности изменения температуры грунта от размерности конечно – разностной сетки и количества лет в расчетах.

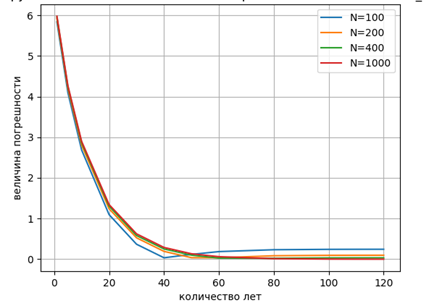
Рисунок 5 - Зависимость накопительной погрешности изменения температуры грунта от числа разбиений и количества лет

Из рис. 5 следует, что погрешность связана в первую очередь с количеством лет в расчетах, а не с размерностью конечно – разностной сетки. Достаточная точность может достигаться и при размерности 100-200 элементов.

Выводы. Проведенные расчеты показывают, что процесс промерзания грунта в первую очередь зависит от температуры на границе, а также от глубины грунта. Вторым важным фактором является продолжительность сезонов, зависящая от географической широты региона. При низкой среднегодовой температуре возможна сезонная мерзлота при продолжительном воздействии положительной температуры. Стационарное состояние температуры грунта наступает приблизительно через 8 лет при неизменных условиях и практически не зависит от размерности конечно – разностной сетки.

Заключение. Построена математическая модель, основанная на уравнении теплопроводности с применением зонального осреднения параметров по широте и учитывающая наличие обратной альбедо-температурной связи. Предлагаемый конечно – разностный метод решения полученных уравнений, имеет преимущество в том, что он не зависит от выбора коэффициентов поглощения климатической системы, характера зависимости длинноволнового излучения от температуры и других факторов и допускает произвольную нелинейную зависимость коэффициента диффузии от широты и температуры.

С применением данной модели были изучены зависимости, возникающие в рассматриваемой модели, в частности, проведены численные эксперименты по изучению теоретически возможных изменений температурного режима Земли при изменении климата.