Дифференцирование и интегрирование тригонометрических функций на основе тригонометрической теории чисел.
Введение.
Не секрет, что высшая математика в большинстве своём имеет дело с приближенными вычислениями и позволяет производить и получать приближённые результаты в вычислениях с достаточной степенью точности.
Но какова эта достаточная степень точности?
Для ответа на этот вопрос, ответим сначала на другие два вопроса.
Вопрос 1: при каком значении числа N второй замечательный предел 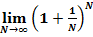 становится числом
становится числом 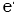 ?
?
Довольно простые расчёты позволяют определить величину числа N, оно будет равно:
N = 253 = 9007199254740990 = 9,0072E+15.
Вопрос 2: при каком значении угла x выполняется первый замечательный предел 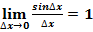 ?
?
Значение угла x° будет равно:
x° = 6,03709E-07 = 0,0000006037.
Таким образом, при числах N ≥ 9007199254740990 и углах x° ≤ 0,0000006037°, можно смело говорить, что высшая математика – точная наука. При других значениях чисел N и углах x° так сказать уже трудно и нельзя. Точная наука математика перестаёт быть точной наукой.
Данная работа направлена на преодоление такого мнения.
1. Основы тригонометрической теории чисел.
Рассмотрим спираль Феодора Киренского в прямоугольной (декартовой) системе координат.
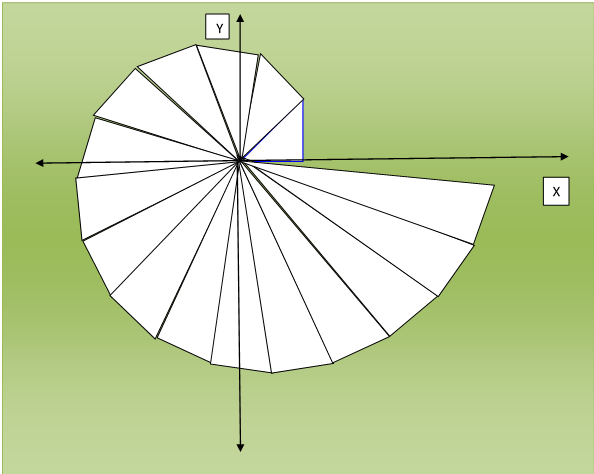
Рисунок № 1. Спираль Феодора Киренского.
Гипотенузы прямоугольных треугольников, из которых состоит спираль, равны квадратному корню из натуральных чисел от единицы до бесконечности, один из катетов всегда равен единице, второй катет последующего треугольника всегда является гипотенузой предыдущего треугольника.
Спираль Феодора Киренского наглядно показывает существование иррациональных чисел, квадратами которых являются натуральные числа, и трансцендентных чисел- углов в треугольниках, которые можно построить, но невозможно точно вычислить.
Спираль Феодора Киренского даёт возможность создать новый раздел математики – новую теорию чисел, тригонометрическую теорию чисел или волновую арифметику на основе элементарной арифметики, элементарной алгебры, геометрии и тригонометрии.
Но вернёмся к нашему доказательству.
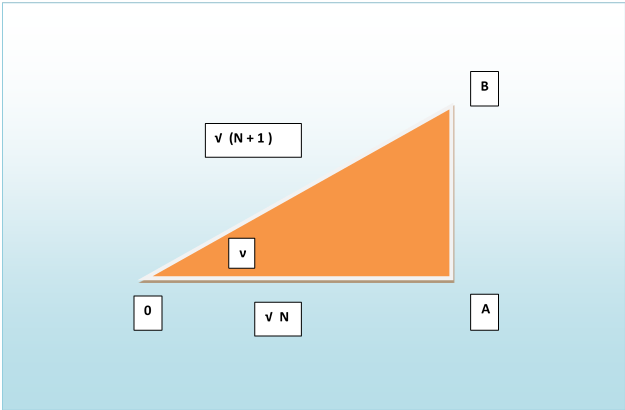
Рисунок № 2. Треугольник.
Рассмотрим какой-либо прямоугольный треугольник (рисунок № 2) из спирали Феодора Киренского.
Будем считать, что катет AB равен 1.
Катет 0A равен √N, где N – числа натурального ряда.
На основании теоремы Пифагора гипотенуза 0B равна √(N + 1).
Угол, лежащий напротив катета AB, назовём ν (ню).
Тогда тангенс угла ν равняется: tg ν = 1 / √N.
Синус угла ν равняется: sin ν = 1 / √(N + 1).
Косинус угла ν равняется: cos ν = √N / √(N + 1).
Если Ni – любое натуральное число, то на основании любого треугольника спирали Феодора Киренского получаются простые формулы – тригонометрические формулы чисел:
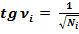 (1)
(1)
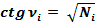 (2)
(2)
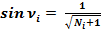 (3)
(3)
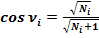 (4)
(4)
Формулы двойных углов:
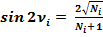 (5)
(5)
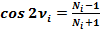 (6)
(6)
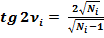 (7)
(7)
Формулы половинных углов:
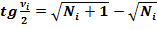 (8)
(8)
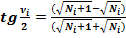 (9)
(9)
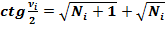 (10)
(10)
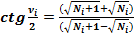 (11)
(11)
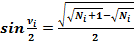 (12)
(12)
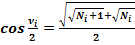 (13)
(13)
Угол ν (ню).
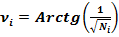 (14)
(14)
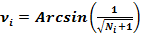 (15)
(15)
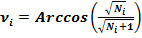 (16)
(16) 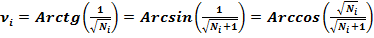
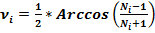 (17)
(17)
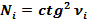 (18)
(18)
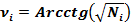 (19)
(19)
Таким образом, каждое натуральное число является квадратом котангенса угла ν, который в свою очередь равен арккотангенсу из квадратного корня данного числа.
Таблица 1. Чиcла N, тангенсы угла ν, угол ν°.
|
№№ |
N |
√ N |
1 / √ N |
ν = arctg (1 / √ N) |
ν° |
|
1 |
1 |
1 |
1 |
0,785398163 |
45 |
|
2 |
2 |
1,414213562 |
0,707106781 |
0,615479709 |
35,26438968 |
|
3 |
3 |
1,732050808 |
0,577350269 |
0,523598776 |
30 |
|
4 |
4 |
2 |
0,5 |
0,463647609 |
26,56505118 |
|
5 |
5 |
2,236067977 |
0,447213595 |
0,420534335 |
24,09484255 |
|
6 |
6 |
2,449489743 |
0,40824829 |
0,387596687 |
22,2076543 |
|
7 |
7 |
2,645751311 |
0,377964473 |
0,361367124 |
20,70481105 |
|
8 |
8 |
2,828427125 |
0,353553391 |
0,339836909 |
19,47122063 |
|
9 |
9 |
3 |
0,333333333 |
0,321750554 |
18,43494882 |
|
10 |
10 |
3,16227766 |
0,316227766 |
0,306277369 |
17,54840061 |
|
11 |
11 |
3,31662479 |
0,301511345 |
0,292842772 |
16,77865488 |
|
12 |
12 |
3,464101615 |
0,288675135 |
0,281034902 |
16,10211375 |
|
13 |
13 |
3,605551275 |
0,277350098 |
0,270549763 |
15,50135957 |
|
14 |
14 |
3,741657387 |
0,267261242 |
0,261157411 |
14,96321743 |
|
15 |
15 |
3,872983346 |
0,25819889 |
0,252680255 |
14,47751219 |
|
16 |
16 |
4 |
0,25 |
0,244978663 |
14,03624347 |
|
17 |
17 |
4,123105626 |
0,242535625 |
0,237941125 |
13,63302223 |
|
18 |
18 |
4,242640687 |
0,23570226 |
0,231477364 |
13,26267601 |
|
19 |
19 |
4,358898944 |
0,229415734 |
0,225513406 |
12,92096638 |
|
20 |
20 |
4,472135955 |
0,223606798 |
0,219987977 |
12,60438265 |
|
21 |
21 |
4,582575695 |
0,21821789 |
0,214849833 |
12,30998866 |
|
22 |
22 |
4,69041576 |
0,213200716 |
0,210055739 |
12,03530731 |
|
23 |
23 |
4,795831523 |
0,208514414 |
0,205568931 |
11,77823215 |
|
24 |
24 |
4,898979486 |
0,204124145 |
0,201357921 |
11,53695903 |
|
25 |
25 |
5 |
0,2 |
0,19739556 |
11,30993247 |
|
26 |
26 |
5,099019514 |
0,196116135 |
0,1936583 |
11,09580328 |
|
27 |
27 |
5,196152423 |
0,19245009 |
0,190125603 |
10,89339465 |
|
28 |
28 |
5,291502622 |
0,188982237 |
0,186779461 |
10,70167482 |
|
29 |
29 |
5,385164807 |
0,185695338 |
0,18360401 |
10,51973489 |
|
30 |
30 |
5,477225575 |
0,182574186 |
0,180585214 |
10,34677062 |
|
31 |
31 |
5,567764363 |
0,179605302 |
0,177710601 |
10,1820674 |
|
32 |
32 |
5,656854249 |
0,176776695 |
0,174969046 |
10,02498786 |
|
33 |
33 |
5,744562647 |
0,174077656 |
0,17235059 |
9,874961398 |
|
34 |
34 |
5,830951895 |
0,171498585 |
0,169846288 |
9,731475473 |
|
35 |
35 |
5,916079783 |
0,169030851 |
0,167448079 |
9,594068227 |
|
36 |
36 |
6 |
0,166666667 |
0,165148677 |
9,462322208 |
|
37 |
37 |
6,08276253 |
0,164398987 |
0,162941479 |
9,335859032 |
|
38 |
38 |
6,164414003 |
0,162221421 |
0,160820481 |
9,214334802 |
|
39 |
39 |
6,244997998 |
0,160128154 |
0,158780215 |
9,097436169 |
|
40 |
40 |
6,32455532 |
0,158113883 |
0,156815685 |
8,984876932 |
Докажем, что полученные формулы являются формулами тригонометрическими.
Основная формула тригонометрии гласит, что сумма квадратов синуса и косинуса любого угла равна единице:
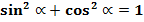
В нашем случае:
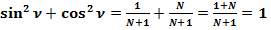 (20)
(20)
Таким образом, сумма квадратов синуса угла ν и косинуса угла ν равна единице, то есть формулы, полученные на основании треугольников спирали Феодора Киренского являются тригонометрическими формулами.
Не менее интересна следующая формула, хотя она не является одной из основных формул тригонометрии.
Известно, что сумма квадрата синуса и квадрата косинуса любого угла равна единице.
А чему равна сумма квадратов косеканса и секанса любого угла?
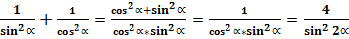
В то же время, произведение квадратов косеканса и секанса любого угла равняется:
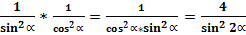
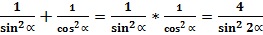
Таким образом, сумма квадратов косеканса и секанса любого угла равна произведению квадратов косеканса и секанса любого угла и равна четырём квадратам косеканса двойного угла.
Выполним вторую проверку.
В нашем случае:
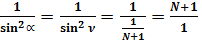 (21)
(21)
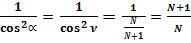 (22)
(22)
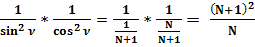 (23)
(23)
 (24)
(24)
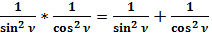
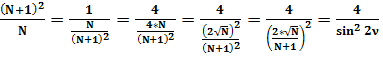 (25)
(25)
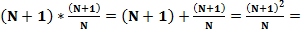
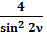
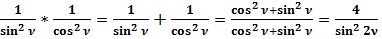 (26)
(26)
Таким образом, сумма квадратов косеканса и секанса угла ν равна произведению квадратов косеканса и секанса угла ν и равна четырём квадратам косеканса двойного угла ν, то есть формулы, полученные на основании треугольников спирали Феодора Киренского являются тригонометрическими формулами.
И самое главное, получена формула (26), в которой произведение чисел равно их сложению.
Выводы:
Каждому числу N соответствует значение тригонометрической функции угла ν:
ctg2 νi = Ni,
или: 1 / tg2 νi = Ni
При N → ∞, угол ν → 0.
При N = 1, угол ν = π/4, или 45°.
При N → 0, угол ν → π/2, или 90°.
Вся числовая ось от нуля до бесконечности заключена между 90° и 0°.
Каждому значению числа N соответствует определённая функция угла ν.
Каждому значению угла ν соответствует определённая функция числа N.
В этом как раз и заключена двойственная природа чисел.
2. Дифференциалы.
2.1. Продифференцируем формулу (1): 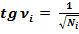
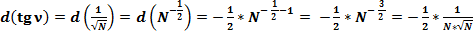 (27)
(27)
Так как: 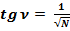 , то:
, то:
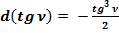 (28)
(28)
Общепринятое значение d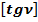 :
:
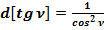 (29)
(29)
Отношение общепринятого значения дифференциала (28) к полученному значению (29) равно:
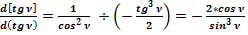 (30)
(30)
2.2. Продифференцируем формулу (3): 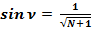
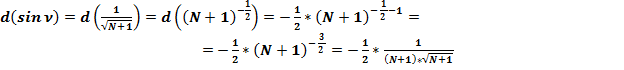 (31)
(31)
Так как: 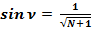 , то:
, то:
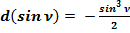 (32)
(32)
Общепринятое значение 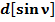 :
:
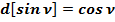 (33)
(33)
Отношение общепринятого значения дифференциала (33) к полученному значению (32) равно:
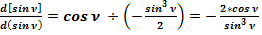 (34)
(34)
2.3. Продифференцируем формулу (4): 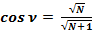
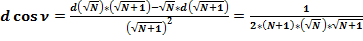 (35)
(35)
Так как: 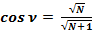 , то:
, то:
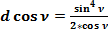 (36)
(36)
Общепринятое значение 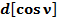 :
:
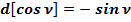 (37)
(37)
Отношение общепринятого значения дифференциала (37) к полученному значению (36) равно:
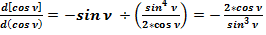 (38)
(38)
2.4. Продифференцируем формулу (2): 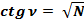
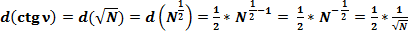 (39)
(39)
Так как: 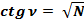 , то:
, то:
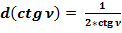 (40)
(40)
Общепринятое значение d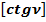 :
:
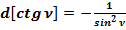 (41)
(41)
Отношение общепринятого значения дифференциала (41) к полученному значению (40) равно:
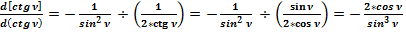 (42)
(42)
2.5. Вычислим значения sin ν, Δ sin ν, d sin ν, cos ν, значения сведём в таблицу № 2,
где:
Δ ν = ν2 – ν1;
Δ sin ν = sin ν2 – sin ν1 ;
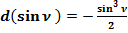 ;
;
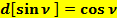 .
.
Таблица 2. Значения ν, Δ sin ν, d(sin ν), d[sin ν].
|
N |
Δ ν |
Δ (sin ν) |
d (sin ν) = -sin³ ν / 2 |
Δ (sin ν) |
d [sin ν] = cos ν |
|
1 |
0,785398163 |
-0,176776695 |
0 |
0,707106781 |
|
|
2 |
-0,169918455 |
-0,129756512 |
-0,096225045 |
-0,129756512 |
0,816496581 |
|
3 |
-0,091880933 |
-0,077350269 |
-0,0625 |
-0,077350269 |
0,866025404 |
|
4 |
-0,059951167 |
-0,052786405 |
-0,04472136 |
-0,052786405 |
0,894427191 |
|
5 |
-0,043113274 |
-0,038965305 |
-0,034020691 |
-0,038965305 |
0,912870929 |
|
6 |
-0,032937649 |
-0,030283817 |
-0,026997462 |
-0,030283817 |
0,9258201 |
|
7 |
-0,026229563 |
-0,024411082 |
-0,022097087 |
-0,024411082 |
0,935414347 |
|
8 |
-0,021530214 |
-0,020220057 |
-0,018518519 |
-0,020220057 |
0,942809042 |
|
9 |
-0,018086355 |
-0,017105567 |
-0,015811388 |
-0,017105567 |
0,948683298 |
|
10 |
-0,015473185 |
-0,014716421 |
-0,013705061 |
-0,014716421 |
0,953462589 |
|
11 |
-0,013434597 |
-0,01283621 |
-0,012028131 |
-0,01283621 |
0,957427108 |
|
12 |
-0,01180787 |
-0,011325036 |
-0,010667311 |
-0,011325036 |
0,960768923 |
|
13 |
-0,010485139 |
-0,010088856 |
-0,009545044 |
-0,010088856 |
0,963624112 |
|
14 |
-0,009392352 |
-0,009062352 |
-0,00860663 |
-0,009062352 |
0,966091783 |
|
15 |
-0,008477156 |
-0,00819889 |
-0,0078125 |
-0,00819889 |
0,968245837 |
|
16 |
-0,007701592 |
-0,007464375 |
-0,007133401 |
-0,007464375 |
0,9701425 |
|
17 |
-0,007037538 |
-0,006833365 |
-0,006547285 |
-0,006833365 |
0,971825316 |
|
18 |
-0,006463761 |
-0,006286527 |
-0,006037256 |
-0,006286527 |
0,973328527 |
|
19 |
-0,005963958 |
-0,005808936 |
-0,00559017 |
-0,005808936 |
0,974679434 |
|
20 |
-0,005525429 |
-0,005388908 |
-0,005195664 |
-0,005388908 |
0,975900073 |
|
21 |
-0,005138144 |
-0,005017174 |
-0,004845471 |
-0,005017174 |
0,977008421 |
|
22 |
-0,004794094 |
-0,004686302 |
-0,004532922 |
-0,004686302 |
0,978019294 |
|
23 |
-0,004486808 |
-0,004390269 |
-0,004252586 |
-0,004390269 |
0,97894501 |
|
24 |
-0,00421101 |
-0,004124145 |
-0,004 |
-0,004124145 |
0,979795897 |
|
25 |
-0,003962361 |
-0,003883865 |
-0,003771464 |
-0,003883865 |
0,980580676 |
|
26 |
-0,003737259 |
-0,003666045 |
-0,003563891 |
-0,003666045 |
0,981306763 |
|
27 |
-0,003532697 |
-0,003467853 |
-0,003374683 |
-0,003467853 |
0,981980506 |
|
28 |
-0,003346142 |
-0,003286898 |
-0,003201644 |
-0,003286898 |
0,982607369 |
|
29 |
-0,003175451 |
-0,003121152 |
-0,003042903 |
-0,003121152 |
0,98319208 |
|
30 |
-0,003018796 |
-0,002968884 |
-0,00289686 |
-0,002968884 |
0,983738754 |
|
31 |
-0,002874613 |
-0,002828607 |
-0,002762136 |
-0,002828607 |
0,984250984 |
|
32 |
-0,002741555 |
-0,002699039 |
-0,00263754 |
-0,002699039 |
0,984731928 |
|
33 |
-0,002618456 |
-0,002579071 |
-0,002522038 |
-0,002579071 |
0,985184366 |
|
287 |
-0,000102747 |
-0,000102569 |
-0,000102301 |
-0,000102569 |
0,998262379 |
|
288 |
-0,000102213 |
-0,000102036 |
-0,000101771 |
-0,000102036 |
0,998268397 |
|
289 |
-0,000101683 |
-0,000101507 |
-0,000101245 |
-0,000101507 |
0,998274373 |
|
290 |
-0,000101158 |
-0,000100984 |
-0,000100723 |
-0,000100984 |
0,998280308 |
|
Σ |
0,058654665 |
-0,648485743 |
-0,747616955 |
-0,648485743 |
287,2762485 |
|
N |
Δ ν |
Δ (sin ν) |
d (sin ν) = -sin³ ν / 2 |
Δ (sin ν) |
d (sin ν) = cos ν |
С увеличением N значения Δ sin ν и d sin ν становятся практически равными, в отличие от общепринятого значения.
Аналогичные значения получаются и при сравнении Δ cos ν и d cos ν,
Δ tg ν и d tg ν, Δ ctg ν и d ctg ν.
Отношение общепринятых значений дифференциалов к полученным значениям всегда равно:
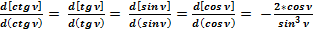 (43)
(43)
Вывод: общепринятые значения дифференциалов тригонометрических функций подсчитаны не правильно.
2.6. Формулы дифференциалов тригонометрических функций.
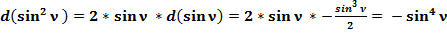 (44)
(44)
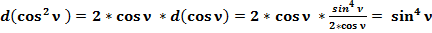 (45)
(45)
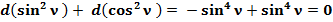 (46)
(46)
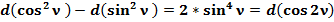
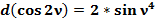 (47)
(47)
Общепринятое значение 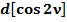 :
:
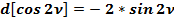 (48)
(48)
Отношение общепринятого значения дифференциала (48) к полученному значению (47) равно:
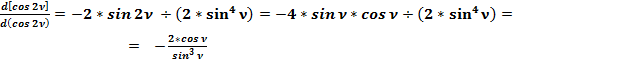
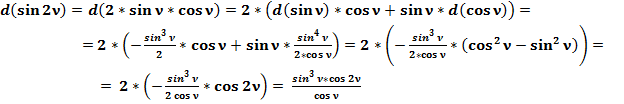 (49)
(49)
Общепринятое значение 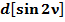 :
:
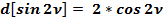 (50)
(50)
Отношение общепринятого значения дифференциала (50) к полученному значению (49) равно:
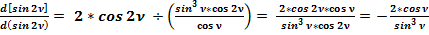
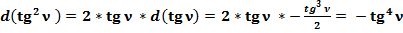 (51)
(51)
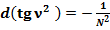
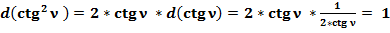 (52)
(52)
В нашем случае: 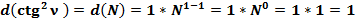
В числовом ряде натуральных чисел разница между последующим и предыдущими числами всегда равна единице.
Δ N = (N + 1) – N = 1
Общепринятое значение 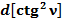 :
:
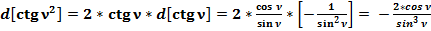 (53)
(53)
Общепринятое значение дифференциала квадрата котангенса угла ν 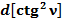 значительно отлично от единицы:
значительно отлично от единицы: 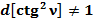 .
.
Отношение общепринятого значения дифференциала (53) к полученному значению (52) равно:
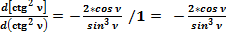
Таблица 3. N, значения дифференциалов d [ctg ν] , d [ctg² ν], d (ctg ν) , d (ctg² ν).
|
N |
d [ctg ν] = - 1 / sin² ν |
d [ctg² ν] |
d (ctg ν) = 1 / (2 * √ N) |
d (ctg² ν) |
|
(- 1) * (N + 1) |
( - 2) * cos ν / sin³ ν |
tg ν / 2 |
Δ N |
|
|
1 |
-2 |
-4 |
0,5 |
1 |
|
2 |
-3 |
-8,485281374 |
0,353553391 |
1 |
|
3 |
-4 |
-13,85640646 |
0,288675135 |
1 |
|
4 |
-5 |
-20 |
0,25 |
1 |
|
5 |
-6 |
-26,83281573 |
0,223606798 |
1 |
|
6 |
-7 |
-34,2928564 |
0,204124145 |
1 |
|
7 |
-8 |
-42,33202098 |
0,188982237 |
1 |
|
8 |
-9 |
-50,91168825 |
0,176776695 |
1 |
|
9 |
-10 |
-60 |
0,166666667 |
1 |
|
10 |
-11 |
-69,57010852 |
0,158113883 |
1 |
|
11 |
-12 |
-79,59899497 |
0,150755672 |
1 |
|
12 |
-13 |
-90,06664199 |
0,144337567 |
1 |
|
13 |
-14 |
-100,9554357 |
0,138675049 |
1 |
|
14 |
-15 |
-112,2497216 |
0,133630621 |
1 |
|
15 |
-16 |
-123,9354671 |
0,129099445 |
1 |
|
16 |
-17 |
-136 |
0,125 |
1 |
|
17 |
-18 |
-148,4318025 |
0,121267813 |
1 |
|
18 |
-19 |
-161,2203461 |
0,11785113 |
1 |
|
19 |
-20 |
-174,3559577 |
0,114707867 |
1 |
|
20 |
-21 |
-187,8297101 |
0,111803399 |
1 |
|
21 |
-22 |
-201,6333306 |
0,109108945 |
1 |
|
22 |
-23 |
-215,759125 |
0,106600358 |
1 |
|
23 |
-24 |
-230,1999131 |
0,104257207 |
1 |
|
24 |
-25 |
-244,9489743 |
0,102062073 |
1 |
|
25 |
-26 |
-260 |
0,1 |
1 |
|
26 |
-27 |
-275,3470537 |
0,098058068 |
1 |
|
27 |
-28 |
-290,9845357 |
0,096225045 |
1 |
|
28 |
-29 |
-306,9071521 |
0,094491118 |
1 |
|
29 |
-30 |
-323,1098884 |
0,092847669 |
1 |
|
30 |
-31 |
-339,5879857 |
0,091287093 |
1 |
|
31 |
-32 |
-356,3369192 |
0,089802651 |
1 |
|
32 |
-33 |
-373,3523805 |
0,088388348 |
1 |
|
33 |
-34 |
-390,63026 |
0,087038828 |
1 |
|
34 |
-35 |
-408,1666326 |
0,085749293 |
1 |
|
35 |
-36 |
-425,9577444 |
0,084515425 |
1 |
|
36 |
-37 |
-444 |
0,083333333 |
1 |
|
37 |
-38 |
-462,2899523 |
0,082199494 |
1 |
|
38 |
-39 |
-480,8242922 |
0,081110711 |
1 |
Таким образом, отношение общепринятых значений дифференциалов к полученным значениям дифференциалов тригонометрических функций всегда равно: 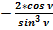 .
.
3. Интеграл (первообразная функция).
∫ d (sin ν) = sin ν
∫ d (sin² ν) = sin² ν
∫ d (tg² ν) = tg² ν = 1 / N = ∫ d (1 / N)
∫ d (ctg² ν) = ctg² ν = N = ∫ d N
3.1. Найдём первообразную функцию формулы (3):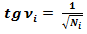 .
.
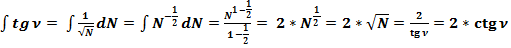 (54)
(54)
Общепринятое значение 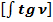 :
:
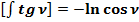 (55)
(55)
Отношение общепринятого значения интеграла (55) к полученному значению (54) равно:
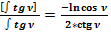 .
.
Дважды продифференцируем 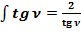 и
и 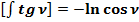 и сравним отношение:
и сравним отношение:
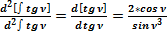 , что соответствует ранее полученному результату.
, что соответствует ранее полученному результату.
3.2. Найдём первообразную функцию формулы (3): 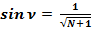 .
.
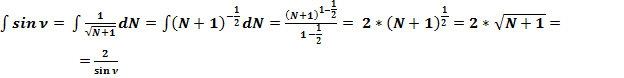 (56)
(56)
Общепринятое значение 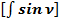 :
:
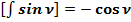 (57)
(57)
Отношение общепринятого значения интеграла (57) к полученному значению (56) равно:
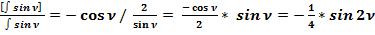 (55)
(55)
Дважды продифференцируем 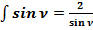 и
и 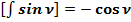 и сравним отношение:
и сравним отношение:
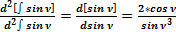 , что соответствует ранее полученному результату.
, что соответствует ранее полученному результату.
3.3. Найдём первообразную функцию формулы (3):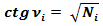 .
.
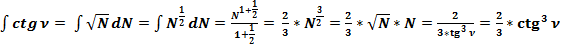 (56) Общепринятое значение
(56) Общепринятое значение 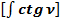 :
:
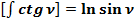 (57)
(57)
Отношение общепринятого значения интеграла (57) к полученному значению (56) равно:
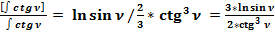
3.4. Найдём первообразную функцию формулы (18):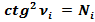 .
.
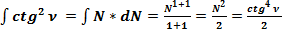 (58)
(58)
Общепринятое значение 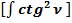 :
:
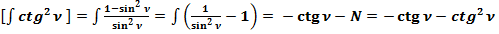 (59)
(59)
Отношение общепринятого значения интеграла (59) к полученному значению (58) равно:
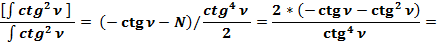
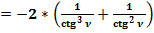
3.5. Сравним отношения интегралов: 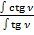 :
:
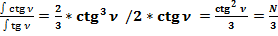
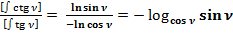
3.6. Найдём первообразную функцию формулы: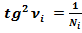 .
.
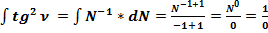 (60)
(60)
Общепринятое значение 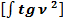 :
:
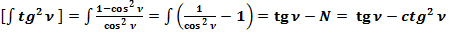 (61)
(61)
3.7. Найдём первообразную функцию формулы: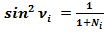 .
.
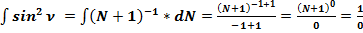 (62)
(62)
3.8. Определим фактическое (реальное) значение интеграла 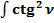 .
.
Известно, сумма членов натурального ряда: 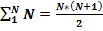 .
.
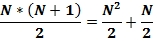
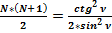
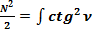
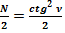
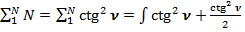
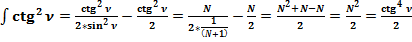
Общепринятое значение 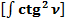 :
:
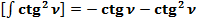
Разница между фактическим (реальным) значением 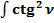 и общепринятым значением составляет:
и общепринятым значением составляет:
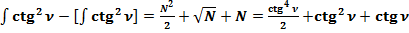 (63) .
(63) .
4. Заключение.
Тригонометрическая теория чисел позволяет определить точные значения тригонометрических функций синуса, косинуса, тангенса и котангенса на основе натуральных чисел.
Тригонометрическая теория чисел позволяет точно определить значения производных и интегралов (первообразных функций) тригонометрических функций.
Дифференцирование и интегрирование тригонометрических функций на основе тригонометрической теории чисел выявили несоответствие общепринятых значений дифференциалов и интегралов их правильным (реальным) значениям.
