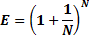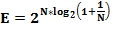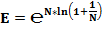Scientific journal
Scientific Review. Fundamental and Applied Research

Personal portfolio

ABOUT THE "NUMBER" e AND ITS DERIVATIVES.

Kolodin A.V. 1
1 no
Is there a number ?? Yes, the number ? - exist. First, as the limit of the sum of the number of: ?=?_(N=0)^??1/N! . Second, as the limit only some of the numbers, that is, a small amount, the second remarkable limit: ?= ?lim??(N??)??(1+1/N)^N ? , if these numbers formed from the numbers 2 exponentiation, a value of 5,6295 E+14 ? N ? 9,0072 E+15 , EN = ? = 2,718281828459050. If N? 9,0072 E+15, the second remarkable limit becomes equal to one. That is the limit of the second remarkable limit when N ? ? is equal to one, and not the number of ?. Hence, neither of which is identical with the convergence of these series cannot be considered. Accepted in any course of mathematical analysis we prove that the function ?x coincides with its derivative (?x): ?x = (?x). But the solution is not unique, and meaningful. And actual computation of the derivatives is even number: ?=?_(N=0)^??1/N! when ?X ? 0,00000001 - confirmed not accepted the value of ?x = (?x), and completely different: ?x ? (?x). The values of the derivatives calculated on the basis of a second remarkable limit: ?= ?lim??(N??)??(1+1/N)^N ?, - when N ? ? , tend to zero: (EN) ? 0, i.e. (EN)? ?. Which again confirms a significant difference between the ranks: ?_(N=0)^??1/N! and ?lim??(N??)??(1+1/N)^N ?. Thus, the necessary revision of many topics and applications of mathematics, especially based on the number of ?.
the number e
the sum of the series
the second remarkable limit
derivative.

О «числе» и его производных.

1. Введение.

Что известно о числе ?

Из Википедии – свободной энциклопедии узнаём, что:

«Число - основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Иногда его называют числом Эйлера или числом Непера».

Приводится «первые тысяча знаков после запятой числа :

2,7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003059921 8174135966 2904357290 0334295260 5956307381 3232862794 3490763233 8298807531 9525101901 1573834187 9307021540 8914993488 4167509244 7614606680 8226480016 8477411853 7423454424 3710753907 7744992069 5517027618 3860626133 1384583000 7520449338 2656029760 6737113200 7093287091 2744374704 7230696977 2093101416 9283681902 5515108657 4637721112 5238978442 5056953696 7707854499 6996794686 4454905987 9316368892 3009879312 7736178215 4249992295 7635148220 8269895193 6680331825 2886939849 6465105820 9392398294 8879332036 2509443117 3012381970 6841614039 7019837679 3206832823 7646480429 5311802328 7825098194 5581530175 6717361332 0698112509 9618188159 3041690351 5988885193 4580727386 6738589422 8792284998 9208680582 5749279610 4841984443 6346324496 8487560233 6248270419 7862320900 2160990235 3043699418 4914631409 3431738143 6405462531 5209618369 0888707016 7683964243 7814059271 4563549061 3031072085 1038375051 0115747704 1718986106 8739696552 1267154688 9570350354».

В настоящее время известно свыше триллиона точных знаков после запятой.

Считается, что впервые нашёл это число Якоб Бернулли, решая задачу о сложных процентах в 1690 году.

Правда, ранее был Непер, Ньютон, Лейбниц, который называл это число буквой “b”.

Букву “e” применил Эйлер в 1737 году. Он и вычислил это число с точностью до 8 знака после запятой: 2,718281828.

Для запоминания: два и семь, дважды дата рождения Льва Толстого, углы прямоугольного треугольника: 45°, 90° и 45°.

В моём компьютере всего лишь тринадцать точных знаков после запятой: 2,718281828459050, - но, думаю, для расчётов этого вполне достаточно, ведь логарифмическая линейка имеет точность всего три знака.

Число можно определить различными способами:

1. как сумму ряда:

.

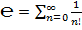2. через предел (второй замечательный предел):

;

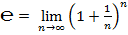Благодаря тому, что 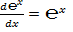и 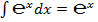, число  является краеугольным камнем в математическом анализе.

Но так ли это в действительности?

Проверке этих общепринятых значений и посвящена данная работа.

2. Число , как сумма ряда: .

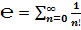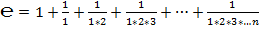, или:

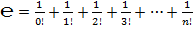
Считается, что первым, кто просуммировал этот ряд и получил результат, был Исаак Ньютон в 1665 году. И, действительно, Тейлор и Маклорен появились на свет значительно позже. Но, как не странно, формулы разложения функций в степенные ряды носят их имена, в отличие от Ньютона, именем которого названа совсем другая формула: бином Ньютона: 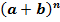или в нашем случае: 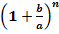, - то есть сумма двух чисел в любой степени.

Примечание: в отличие от общепринятых обозначений, целые числа будут писаться с большой буквы N, с маленькой буквой n – любые действительные числа.

Посчитаем, к чему стремится сумма ряда: .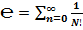

где N = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, … , ∞.

.

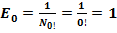
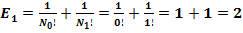
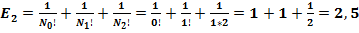Расчёты будем вести в табличной форме.

В нашем случае каждое последующее Nn + 1 будет образовываться от предыдущего Nn прибавлением единицы:

Nn+1 = Nn + 1

Таблица 1.

N

N!

1 / N!

E
       

0

1

1

1

1

1

1

2

2

2

0,5

2,5

3

6

0,166666667

2,666666666666670

4

24

0,041666667

2,708333333333330

5

120

0,008333333

2,716666666666670

6

720

0,001388889

2,718055555555560

7

5040

0,000198413

2,718253968253970

8

40320

2,48016E-05

2,718278769841270

9

362880

2,75573E-06

2,718281525573190

10

3628800

2,75573E-07

2,718281801146380

11

39916800

2,50521E-08

2,718281826198490

12

479001600

2,08768E-09

2,718281828286170

13

6227020800

1,6059E-10

2,718281828446760

14

87178291200

1,14707E-11

2,718281828458230

15

1,30767E+12

7,64716E-13

2,718281828458990

16

2,09228E+13

4,77948E-14

2,718281828459040

17

3,55687E+14

2,81146E-15

2,718281828459050

18

6,40237E+15

1,56192E-16

2,718281828459050

19

1,21645E+17

8,22064E-18

2,718281828459050

20

2,4329E+18

4,11032E-19

2,718281828459050

21

5,10909E+19

1,95729E-20

2,718281828459050

22

1,124E+21

8,89679E-22

2,718281828459050

23

2,5852E+22

3,86817E-23

2,718281828459050

24

6,20448E+23

1,61174E-24

2,718281828459050

25

1,55112E+25

6,44695E-26

2,718281828459050

26

4,03291E+26

2,4796E-27

2,718281828459050

27

1,08889E+28

9,18369E-29

2,718281828459050

28

3,04888E+29

3,27989E-30

2,718281828459050

29

8,84176E+30

1,131E-31

2,718281828459050

30

2,65253E+32

3,76999E-33

2,718281828459050

 

Таким образом, при числе N, равном 17, значение суммы ряда:

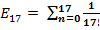= 2,718281828459050, - то есть равно общепринятому значению числа

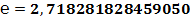. Таким образом, сумма ряда: 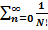действительно стремится к числу и имеет предел, который и называется числом . Следовательно, число - есть.

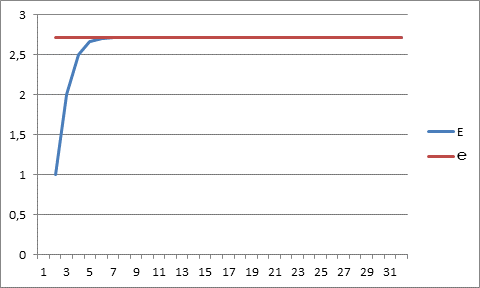
На основании данных таблицы 1 представим график 1.

График 1.

3. Второй замечательный предел и число .

В любом курсе по высшей математике доказывается, что предел числовой последовательности 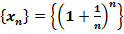, заключён между двумя числами: 2 и 3, то есть, - .

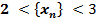Считается, что значение этого предела при n → ∞ и есть число .

,

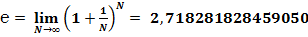где N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, … , ∞.

3.1. Вычисление второго замечательного предела при различных значениях чисел N.

Считаем, что 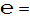2,718281828459050.

Расчёты будем вести в табличной форме.

Каждое последующее Nn + 1 будет образовываться удвоением от предыдущего Nn :

Nn+1 = 2 * Nn .

Для каждого Nn существует значение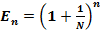

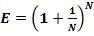при N → ∞ , E → , и в пределе E = .

Таблица 2.

N

Δ
       

1

2,718281828

2

0,718281828

2

2,718281828

2,25

0,468281828

4

2,718281828

2,44140625

0,276875578

8

2,718281828

2,565784514

0,152497315

16

2,718281828

2,637928497

0,080353331

32

2,718281828

2,676990129

0,041291699

64

2,718281828

2,697344953

0,020936876

128

2,718281828

2,70773902

0,010542809

256

2,718281828

2,712991624

0,005290204

512

2,718281828

2,715632

0,002649828

1024

2,718281828

2,716955729

0,001326099

2048

2,718281828

2,717618482

0,000663346

4096

2,718281828

2,717950081

0,000331747

8192

2,718281828

2,718115936

0,000165892

16384

2,718281828

2,718198878

8,29507E-05

32768

2,718281828

2,718240352

4,14765E-05

65536

2,718281828

2,71826109

2,07386E-05

131072

2,718281828

2,718271459

1,03694E-05

262144

2,718281828

2,718276644

5,18469E-06

524288

2,718281828

2,718279236

2,59234E-06

1048576

2,718281828

2,718280532

1,29618E-06

2097152

2,718281828

2,71828118

6,48095E-07

4194304

2,718281828

2,718281504

3,2406E-07

8388608

2,718281828

2,718281666

1,62038E-07

16777216

2,718281828

2,718281747

8,10322E-08

33554432

2,718281828

2,718281788

4,05267E-08

67108864

2,718281828

2,718281808

2,02766E-08

134217728

2,718281828

2,718281808

2,02766E-08

268435456

2,718281828

2,718281808

2,02766E-08

536870912

2,718281828

2,718281808

2,02766E-08

1073741824

2,718281828

2,718281808

2,02766E-08

2147483648

2,718281828

2,718281808

2,02766E-08

4294967296

2,718281828

2,718281828

3,1645E-10

8589934592

2,718281828

2,718281828

1,58225E-10

17179869184

2,718281828

2,718281828

7,91123E-11

34359738368

2,718281828

2,718281828

3,95559E-11

68719476736

2,718281828

2,718281828

1,9778E-11

1,37439E+11

2,718281828

2,718281828

9,88898E-12

2,74878E+11

2,718281828

2,718281828

4,94449E-12

5,49756E+11

2,718281828

2,718281828

2,47224E-12

1,09951E+12

2,718281828

2,718281828

1,2359E-12

2,19902E+12

2,718281828

2,718281828

6,17728E-13

4,39805E+12

2,718281828

2,718281828

3,09086E-13

8,79609E+12

2,718281828

2,718281828

1,54543E-13

1,75922E+13

2,718281828

2,718281828

7,72715E-14

3,51844E+13

2,718281828

2,718281828

3,86358E-14

7,03687E+13

2,718281828

2,718281828

1,90958E-14

1,40737E+14

2,718281828

2,718281828

9,32587E-15

2,81475E+14

2,718281828

2,718281828

4,88498E-15

5,6295E+14

2,718281828

2,718281828

0

1,1259E+15

2,718281828

2,718281828

0

2,2518E+15

2,718281828

2,718281828

0

4,5036E+15

2,718281828

2,718281828

0

9,0072E+15

2,718281828

1

1,718281828

1,80144E+16

2,718281828

1

1,718281828

Примечание: красным цветом выделены значения E = 1.

При значении N = 5,6295E+14, E = = 2,718281828459050.

Таким образом, можно утверждать, что бесконечность начинается с числа N ≥ 5,6295E+14, ведь при таком значении N второй замечательный предел: .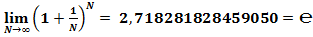

Но при значении N≥ 9,0072E+15, 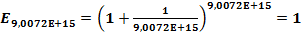, что не равно числу .

Почему значения E получились такими?

Самое простое объяснение такое: 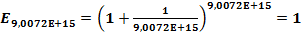, то есть значение в скобках: 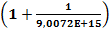при N= 9,0072E+15 становится равным единице, а должно быть больше единицы, значит, так заложено в программном обеспечении компьютера или зависит от мощности компьютера, что уже само по себе неверно. Ниже будет дано объяснение этому явлению.

Но как бы там ни было, значение бесконечности распространяется до N≤ 9,0072E+15.

При числах N≥ 9,0072E+15, именно в бесконечности, второй замечательный предел становится равным единице.

На основании данных таблицы 2, представлен график 2.

График 2.

Проверим полученный результат при нескольких вариантах значения чисел:

числа N2 образуются при помощи умножения каждого предыдущего числа на 2, числа N3 - на 3, числа N5 - на 5, числа N7 - на 7.

Соответственно, по формуле 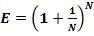вычисляются значения E2 для чисел N2, E3 для чисел N3, E5 для чисел N5, E7 для чисел N7.

Данные представлены в таблице 3.

Таблица 3.

N2

N3

N5

N7

E2

E3

E5

E7
               

1

1

1

1

2

2

2

2

2

3

5

7

2,25

2,37037

2,48832

2,5465

4

9

25

49

2,441406

2,581175

2,665836

2,691053

8

27

125

343

2,565785

2,669594

2,707488

2,71433

16

81

625

2401

2,637928

2,70169

2,71611

2,717716

32

243

3125

16807

2,67699

2,71271

2,717847

2,718201

64

729

15625

117649

2,697345

2,71642

2,718195

2,71827

128

2187

78125

823543

2,707739

2,717661

2,718264

2,71828

256

6561

390625

5764801

2,712992

2,718075

2,718278

2,718282

512

19683

2E+06

4E+07

2,715632

2,718213

2,718281

2,718282

1024

59049

1E+07

2,8E+08

2,716956

2,718259

2,718282

2,718282

2048

177147

5E+07

2E+09

2,717618

2,718274

2,718282

2,718281

4096

531441

2E+08

1,4E+10

2,71795

2,718279

2,718282

2,718279

8192

1594323

1E+09

9,7E+10

2,718116

2,718281

2,718282

2,718279

16384

4782969

6E+09

6,8E+11

2,718199

2,718282

2,718283

2,718162

32768

1,4E+07

3E+10

4,7E+12

2,71824

2,718282

2,718283

2,71939

65536

4,3E+07

2E+11

3,3E+13

2,718261

2,718282

2,718301

2,728004

131072

1,3E+08

8E+11

2,3E+14

2,718271

2,718282

2,718301

2,668276

262144

3,9E+08

4E+12

1,6E+15

2,718277

2,718282

2,719222

2,958674

524288

1,2E+09

2E+13

1,1E+16

2,718279

2,718282

2,71692

1

1048576

3,5E+09

1E+14

8E+16

2,718281

2,718282

2,705438

1

2097152

1E+10

5E+14

5,6E+17

2,718281

2,718282

2,59325

1

4194304

3,1E+10

2E+15

3,9E+18

2,718282

2,718276

2,882884

1

8388608

9,4E+10

1E+16

2,7E+19

2,718282

2,718295

1

1

16777216

2,8E+11

6E+16

1,9E+20

2,718282

2,718295

1

1

33554432

8,5E+11

3E+17

1,3E+21

2,718282

2,718124

1

1

67108864

2,5E+12

1E+18

9,4E+21

2,718282

2,718636

1

1

1,34E+08

7,6E+12

7E+18

6,6E+22

2,718282

2,720171

1

1

2,68E+08

2,3E+13

4E+19

4,6E+23

2,718282

2,720171

1

1

5,37E+08

6,9E+13

2E+20

3,2E+24

2,718282

2,734023

1

1

1,07E+09

2,1E+14

9E+20

2,3E+25

2,718282

2,734023

1

1

2,15E+09

6,2E+14

5E+21

1,6E+26

2,718282

2,611846

1

1

4,29E+09

1,9E+15

2E+22

1,1E+27

2,718282

2,277108

1

1

8,59E+09

5,6E+15

1E+23

7,7E+27

2,718282

3,436177

1

1

1,72E+10

1,7E+16

6E+23

5,4E+28

2,718282

1

1

1

3,44E+10

5E+16

3E+24

3,8E+29

2,718282

1

1

1

6,87E+10

1,5E+17

1E+25

2,7E+30

2,718282

1

1

1

1,37E+11

4,5E+17

7E+25

1,9E+31

2,718282

1

1

1

2,75E+11

1,4E+18

4E+26

1,3E+32

2,718282

1

1

1

5,5E+11

4,1E+18

2E+27

9,1E+32

2,718282

1

1

1

1,1E+12

1,2E+19

9E+27

6,4E+33

2,718282

1

1

1

2,2E+12

3,6E+19

5E+28

4,5E+34

2,718282

1

1

1

4,4E+12

1,1E+20

2E+29

3,1E+35

2,718282

1

1

1

8,8E+12

3,3E+20

1E+30

2,2E+36

2,718282

1

1

1

1,76E+13

9,8E+20

6E+30

1,5E+37

2,718282

1

1

1

3,52E+13

3E+21

3E+31

1,1E+38

2,718282

1

1

1

7,04E+13

8,9E+21

1E+32

7,5E+38

2,718282

1

1

1

1,41E+14

2,7E+22

7E+32

5,2E+39

2,718282

1

1

1

2,81E+14

8E+22

4E+33

3,7E+40

2,718282

1

1

1

5,63E+14

2,4E+23

2E+34

2,6E+41

2,718282

1

1

1

1,13E+15

7,2E+23

9E+34

1,8E+42

2,718282

1

1

1

2,25E+15

2,2E+24

4E+35

1,3E+43

2,718282

1

1

1

4,5E+15

6,5E+24

2E+36

8,8E+43

2,718282

1

1

1

9,01E+15

1,9E+25

1E+37

6,2E+44

1

  

1

1

Примечание: жёлтым цветом выделены значения E > , красным цветом - значения E = 1.

На основании данных таблицы 3 представлен график 3.

График 3.

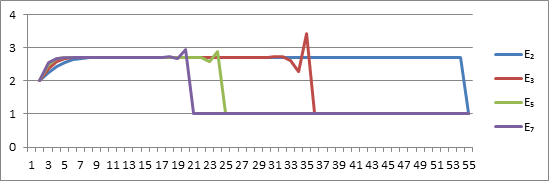
Данные таблицы 2 подтверждают, что при значении N2 ≥ 9,01E+15, значения E2 = 1,

N3 ≥ 1,7E+16; значения E3 = 1;

N5 ≥ 1E+16, значения E5 = 1;

N7 ≥ 1,16E+16, значения E7 = 1.

Значения E3 , E5 и E7 не стремятся к числу , как своему пределу, а имеют свои пределы.

Только значения E2 стремятся к числу , при N = 5,6295E+14 становятся числом , но уже при N2 ≥ 9,01E+15, перестают им быть и становятся равным единице.

Таким образом, второй замечательный предел не имеет предела, равного числу .

Для проверки этого вывода, вычислим значения E по формуле 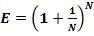, где числа N, начиная с N = 10000000000 (1010) будут увеличиваться на 1000000000 (109).

Таблица 4.

N

E = (1 + 1 / N ) ^ N

Δ = - E

(1 + 1 / N ) n /
         

1

2,718281828

2

0,7182818284590

0,735758882

10

2,718281828

2,59374246

0,1245393683590

0,954184527

100

2,718281828

2,704813829

0,0134679990375

0,9950454

1000

2,718281828

2,716923932

0,0013578962235

0,999500458

10000

2,718281828

2,718145927

0,0001359016347

0,999950005

100000

2,718281828

2,718268237

0,0000135912615

0,999995

1000000

2,718281828

2,718280469

0,0000013593026

0,9999995

10000000

2,718281828

2,718281694

0,0000001344787

0,999999951

100000000

2,718281828

2,718281786

0,0000000420632

0,999999985

1E+09

2,718281828

2,718282031

-0,0000002023555

1,000000074

1E+10

2,718281828

2,718282053

-0,0000002247757

1,000000083

2E+10

2,718281828

2,718282053

-0,0000002248437

1,000000083

3E+10

2,718281828

2,718282053

-0,0000002248664

1,000000083

4E+10

2,718281828

2,718282053

-0,0000002248777

1,000000083

5E+10

2,718281828

2,718282053

-0,0000002248845

1,000000083

6E+10

2,718281828

2,718282053

-0,0000002248890

1,000000083

7E+10

2,718281828

2,718276018

0,0000058108997

0,999997862

8E+10

2,718281828

2,718282053

-0,0000002248947

1,000000083

9E+10

2,718281828

2,718282053

-0,0000002248966

1,000000083

1E+11

2,718281828

2,718282053

-0,0000002248981

1,000000083

2E+11

2,718281828

2,718282053

-0,0000002249049

1,000000083

3E+11

2,718281828

2,718282053

-0,0000002249071

1,000000083

4E+11

2,718281828

2,718282053

-0,0000002249083

1,000000083

5E+11

2,718281828

2,718221696

0,0000601324074

0,999977879

6E+11

2,718281828

2,718282053

-0,0000002249094

1,000000083

7E+11

2,718281828

2,718402772

-0,0001209435631

1,000044493

8E+11

2,718281828

2,718040632

0,0002411963145

0,999911269

9E+11

2,718281828

2,718282053

-0,0000002249101

1,000000083

1E+12

2,718281828

2,718523496

-0,0002416675782

1,000088905

2E+12

2,718281828

2,718523496

-0,0002416675789

1,000088905

3E+12

2,718281828

2,71791993

0,0003618988847

0,999866865

4E+12

2,718281828

2,718523496

-0,0002416675792

1,000088905

5E+12

2,718281828

2,719127197

-0,0008453680767

1,000310994

6E+12

2,718281828

2,719731031

-0,0014492026374

1,000533132

7E+12

2,718281828

2,716713199

0,0015686298305

0,999422933

8E+12

2,718281828

2,718523496

-0,0002416675794

1,000088905

9E+12

2,718281828

2,716110034

0,0021717943722

0,999201042

1E+13

2,718281828

2,716110034

0,0021717943721

0,999201042

2E+13

2,718281828

2,716110034

0,0021717943721

0,999201042

3E+13

2,718281828

2,716110034

0,0021717943721

0,999201042

4E+13

2,718281828

2,728198808

-0,0099169798205

1,003648253

5E+13

2,718281828

2,716110034

0,0021717943720

0,999201042

6E+13

2,718281828

2,716110034

0,0021717943720

0,999201042

7E+13

2,718281828

2,704074826

0,0142070026510

0,994773536

8E+13

2,718281828

2,704074826

0,0142070026510

0,994773536

9E+13

2,718281828

2,716110034

0,0021717943720

0,999201042

1E+14

2,718281828

2,716110034

0,0021717943720

0,999201042

2E+14

2,718281828

2,777094348

-0,0588125198594

1,021635917

3E+14

2,718281828

2,716110034

0,0021717943720

0,999201042

4E+14

2,718281828

2,656464921

0,0618169079441

0,97725883

5E+14

2,718281828

2,716110034

0,0021717943720

0,999201042

6E+14

2,718281828

2,903201529

-0,1849197007248

1,068028156

7E+14

2,718281828

2,541075307

0,1772065213851

0,934809364

8E+14

2,718281828

2,903201529

-0,1849197007248

1,068028156

9E+14

2,718281828

2,716110034

0,0021717943720

0,999201042

1E+15

2,718281828

3,035035207

-0,3167533780902

1,116527056

2E+15

2,718281828

2,430697905

0,2875839237530

0,894203787

3E+15

2,718281828

3,789627122

-1,0713452935126

1,394125908

4E+15

2,718281828

2,430697905

0,2875839237530

0,894203787

5E+15

2,718281828

3,035035207

-0,3167533780902

1,116527056

6E+15

2,718281828

3,789627122

-1,0713452935126

1,394125908

7E+15

2,718281828

4,731831016

-2,0135491870735

1,74074335

8E+15

2,718281828

5,908292304

-3,1900104754832

2,173539271

9E+15

2,718281828

7,377253717

-4,6589718888092

2,713939975

1E+16

2,718281828

1

1,7182818284591

0,367879441

1E+17

2,718281828

1

1,7182818284591

0,367879441

Примечание: жёлтым цветом выделены значения E > , красным цветом - значения E = 1.

На основании данных таблицы 4 представлены графики 4, 5 и 6.

График 4.

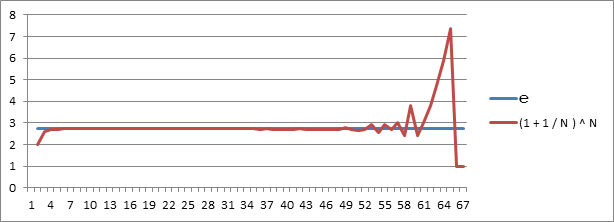
График 5.

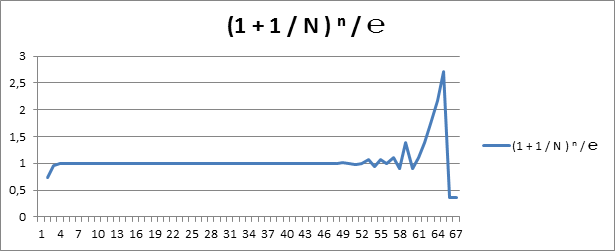
График 6.

3.2. Проверка значений второго замечательного предела при помощи логарифмов.

Для проверки полученных значений второго замечательного предела проверим полученные значения при помощи логарифмов: по основанию 2 и основанию  (натуральных логарифмов).

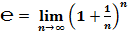
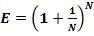
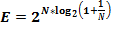
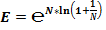
Таблица 5.

N

         

1

2,718281828

2

2

2

2

2,718281828

2,25

2,25

2,25

3

2,718281828

2,37037037

2,37037037

2,37037037

4

2,718281828

2,44140625

2,44140625

2,44140625

5

2,718281828

2,48832

2,48832

2,48832

6

2,718281828

2,521626372

2,521626372

2,521626372

7

2,718281828

2,546499697

2,546499697

2,546499697

8

2,718281828

2,565784514

2,565784514

2,565784514

9

2,718281828

2,581174792

2,581174792

2,581174792

10

2,718281828

2,59374246

2,59374246

2,59374246

20

2,718281828

2,653297705

2,653297705

2,653297705

30

2,718281828

2,674318776

2,674318776

2,674318776

40

2,718281828

2,685063838

2,685063838

2,685063838

50

2,718281828

2,691588029

2,691588029

2,691588029

60

2,718281828

2,695970139

2,695970139

2,695970139

70

2,718281828

2,699116371

2,699116371

2,699116371

80

2,718281828

2,701484941

2,701484941

2,701484941

90

2,718281828

2,703332461

2,703332461

2,703332461

100

2,718281828

2,704813829

2,704813829

2,704813829

200

2,718281828

2,711517123

2,711517123

2,711517123

300

2,718281828

2,713765158

2,713765158

2,713765158

400

2,718281828

2,714891744

2,714891744

2,714891744

500

2,718281828

2,715568521

2,715568521

2,715568521

600

2,718281828

2,716020049

2,716020049

2,716020049

700

2,718281828

2,716342738

2,716342738

2,716342738

800

2,718281828

2,716584847

2,716584847

2,716584847

900

2,718281828

2,716773208

2,716773208

2,716773208

1000

2,718281828

2,716923932

2,716923932

2,716923932

2000

2,718281828

2,717602569

2,717602569

2,717602569

3000

2,718281828

2,71782892

2,71782892

2,71782892

4000

2,718281828

2,717942121

2,717942121

2,717942121

5000

2,718281828

2,71801005

2,71801005

2,71801005

6000

2,718281828

2,71805534

2,71805534

2,71805534

7000

2,718281828

2,718087691

2,718087691

2,718087691

8000

2,718281828

2,718111955

2,718111955

2,718111955

9000

2,718281828

2,718130828

2,718130828

2,718130828

10000

2,718281828

2,718145927

2,718145927

2,718145927

20000

2,718281828

2,718213875

2,718213875

2,718213875

30000

2,718281828

2,718236525

2,718236525

2,718236525

40000

2,718281828

2,718247851

2,718247851

2,718247851

50000

2,718281828

2,718254646

2,718254646

2,718254646

60000

2,718281828

2,718259176

2,718259177

2,718259176

70000

2,718281828

2,718262412

2,718262413

2,718262413

80000

2,718281828

2,718264839

2,718264839

2,71826484

90000

2,718281828

2,718266727

2,718266727

2,718266727

100000

2,718281828

2,718268237

2,718268238

2,718268237

200000

2,718281828

2,718275033

2,718275033

2,718275033

300000

2,718281828

2,718277298

2,718277298

2,718277298

400000

2,718281828

2,71827843

2,718278432

2,71827843

500000

2,718281828

2,71827911

2,71827911

2,71827911

600000

2,718281828

2,718279563

2,718279567

2,718279565

700000

2,718281828

2,718279887

2,718279889

2,718279888

800000

2,718281828

2,71828013

2,718280129

2,71828013

900000

2,718281828

2,718280318

2,718280318

2,718280315

1000000

2,718281828

2,718280469

2,718280469

2,71828047

2000000

2,718281828

2,718281149

2,718281152

2,718281155

3000000

2,718281828

2,718281376

2,718281366

2,718281373

4000000

2,718281828

2,718281489

2,7182815

2,718281493

5000000

2,718281828

2,718281555

2,71828154

2,718281546

6000000

2,718281828

2,718281602

2,718281607

2,71828159

7000000

2,718281828

2,718281634

2,718281627

2,718281628

8000000

2,718281828

2,718281655

2,718281661

2,718281667

9000000

2,718281828

2,71828168

2,718281668

2,718281706

10000000

2,718281828

2,718281694

2,718281674

2,718281667

20000000

2,718281828

2,718281754

2,718281875

2,71828186

30000000

2,718281828

2,71828179

2,718282009

2,718282053

40000000

2,718281828

2,718281803

2,718281607

2,718281667

50000000

2,718281828

2,718281817

2,718281808

2,718282053

60000000

2,718281828

2,718281808

2,718282009

2,718282053

70000000

2,718281828

2,718281836

2,718281674

2,718281764

80000000

2,718281828

2,718281803

2,718281875

2,718281667

90000000

2,718281828

2,718281831

2,71828221

2,718282053

100000000

2,718281828

2,718281786

2,718281473

2,718281088

200000000

2,718281828

2,718281786

2,718282143

2,718282053

300000000

2,718281828

2,718281857

2,718282812

2,718282053

400000000

2,718281828

2,718281786

2,718283482

2,718283985

500000000

2,718281828

2,718281729

2,718281473

2,718282053

600000000

2,718281828

2,718281676

2,718280804

2,718282053

700000000

2,718281828

2,718281922

2,718282143

2,718281088

800000000

2,718281828

2,718282028

2,718280804

2,718283985

900000000

2,718281828

2,718282025

2,718282812

2,718282053

1000000000

2,718281828

2,718282031

2,718278126

2,718282053

2000000000

2,718281828

2,718282031

2,718278126

2,718272396

3000000000

2,718281828

2,718282051

2,718264739

2,718282053

4000000000

2,718281828

2,718282031

2,718291514

2,718291711

5000000000

2,718281828

2,718282053

2,718264739

2,718282053

6000000000

2,718281828

2,718282053

2,718345066

2,718311025

7000000000

2,718281828

2,718280242

2,718197801

2,718233767

8000000000

2,718281828

2,718282053

2,718264739

2,718253082

9000000000

2,718281828

2,718282053

2,718264739

2,718282053

1E+10

2,718281828

2,718282053

2,718264739

2,718233767

2E+10

2,718281828

2,718282053

2,718264739

2,71833034

3E+10

2,718281828

2,718282053

2,717863136

2,718137198

4E+10

2,718281828

2,718282053

2,718264739

2,71833034

5E+10

2,718281828

2,718282053

2,718398619

2,718523496

6E+10

2,718281828

2,718282053

2,718264739

2,718137198

7E+10

2,718281828

2,718276018

2,717729282

2,718233767

8E+10

2,718281828

2,718282053

2,718264739

2,718716666

9E+10

2,718281828

2,718282053

2,719469903

2,718716666

1E+11

2,718281828

2,718282053

2,717729282

2,717557854

2E+11

2,718281828

2,718282053

2,717729282

2,717557854

3E+11

2,718281828

2,718282053

2,719068122

2,717557854

4E+11

2,718281828

2,718282053

2,720407622

2,715627599

5E+11

2,718281828

2,718221696

2,717729282

2,718523496

6E+11

2,718281828

2,718282053

2,715053578

2,717557854

7E+11

2,718281828

2,718402772

2,717729282

2,717557854

8E+11

2,718281828

2,718040632

2,720407622

2,719489481

9E+11

2,718281828

2,718282053

2,723088602

2,72045581

1E+12

2,718281828

2,718523496

2,717729282

2,723356855

2E+12

2,718281828

2,718523496

2,704377082

2,704074826

3E+12

2,718281828

2,71791993

2,691090481

2,723356855

4E+12

2,718281828

2,718523496

2,731147405

2,74277638

5E+12

2,718281828

2,719127197

2,744631777

2,752538009

6E+12

2,718281828

2,719731031

2,731147405

2,723356855

7E+12

2,718281828

2,716713199

2,717729282

2,704074826

8E+12

2,718281828

2,718523496

2,785485663

2,704074826

9E+12

2,718281828

2,716110034

2,651621061

2,694485067

1E+13

2,718281828

2,716110034

2,813058871

2,704074826

2E+13

2,718281828

2,716110034

2,955073509

2,903201529

3E+13

2,718281828

2,716110034

2,426668306

2,60969327

4E+13

2,718281828

2,728198808

2,677869158

2,704074826

5E+13

2,718281828

2,716110034

3,425600329

2,903201529

6E+13

2,718281828

2,716110034

2,426668306

2,903201529

7E+13

2,718281828

2,704074826

2,813058871

2,704074826

8E+13

2,718281828

2,704074826

1,482913235

1,765500445

9E+13

2,718281828

2,716110034

3,780207392

3,592961973

1E+14

2,718281828

2,716110034

1,636419615

2,035095478

2E+14

2,718281828

2,777094348

1

1

3E+14

2,718281828

2,716110034

19,20295481

8,428579119

4E+14

2,718281828

2,656464921

7,170983227

17,15296325

5E+14

2,718281828

2,716110034

11,73473761

34,90791795

6E+14

2,718281828

2,903201529

1

1

7E+14

2,718281828

2,541075307

1

1

8E+14

2,718281828

2,903201529

1

1

9E+14

2,718281828

2,716110034

7081,156291

598,7742338

1E+15

2,718281828

3,035035207

1

1

2E+15

2,718281828

2,430697905

1

1

3E+15

2,718281828

3,789627122

6,81837E+12

1809437884

4E+15

2,718281828

2,430697905

1

1

5E+15

2,718281828

3,035035207

1

1

6E+15

2,718281828

3,789627122

1

1

7E+15

2,718281828

4,731831016

1

1

8E+15

2,718281828

5,908292304

1

1

9E+15

2,718281828

7,377253717

1

1

1E+16

2,718281828

1

1

1

2E+16

2,718281828

1

1

1

3E+16

2,718281828

1

1

1

4E+16

2,718281828

1

1

1

5E+16

2,718281828

1

1

1

6E+16

2,718281828

1

1

1

7E+16

2,718281828

1

1

1

8E+16

2,718281828

1

1

1

9E+16

2,718281828

1

1

1

1E+17

2,718281828

1

1

1

Примечание: жёлтым цветом выделены значения E > , красным цветом - значения E = 1,

синим цветом - значения E < 2.

На основании данных таблицы 5 представим график 7.

График 7.

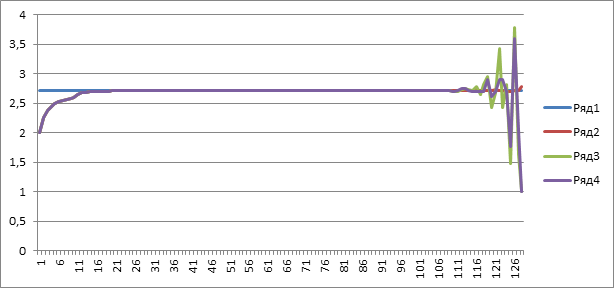
Для большей наглядности полученных результатов преобразуем данные таблицы 5: выберем интервал чисел N от 1,00E+10 до 2,00E+14, - получим таблицу 6.

Таблица 6.

N

         

1,00E+10

2,718282

2,718282

2,718265

2,718234

2,00E+10

2,718282

2,718282

2,718265

2,71833

3,00E+10

2,718282

2,718282

2,717863

2,718137

4,00E+10

2,718282

2,718282

2,718265

2,71833

5,00E+10

2,718282

2,718282

2,718399

2,718523

6,00E+10

2,718282

2,718282

2,718265

2,718137

7,00E+10

2,718282

2,718276

2,717729

2,718234

8,00E+10

2,718282

2,718282

2,718265

2,718717

9,00E+10

2,718282

2,718282

2,71947

2,718717

1,00E+11

2,718282

2,718282

2,717729

2,717558

2,00E+11

2,718282

2,718282

2,717729

2,717558

3,00E+11

2,718282

2,718282

2,719068

2,717558

4,00E+11

2,718282

2,718282

2,720408

2,715628

5,00E+11

2,718282

2,718222

2,717729

2,718523

6,00E+11

2,718282

2,718282

2,715054

2,717558

7,00E+11

2,718282

2,718403

2,717729

2,717558

8,00E+11

2,718282

2,718041

2,720408

2,719489

9,00E+11

2,718282

2,718282

2,723089

2,720456

1,00E+12

2,718282

2,718523

2,717729

2,723357

2,00E+12

2,718282

2,718523

2,704377

2,704075

3,00E+12

2,718282

2,71792

2,69109

2,723357

4,00E+12

2,718282

2,718523

2,731147

2,742776

5,00E+12

2,718282

2,719127

2,744632

2,752538

6,00E+12

2,718282

2,719731

2,731147

2,723357

7,00E+12

2,718282

2,716713

2,717729

2,704075

8,00E+12

2,718282

2,718523

2,785486

2,704075

9,00E+12

2,718282

2,71611

2,651621

2,694485

1,00E+13

2,718282

2,71611

2,813059

2,704075

2,00E+13

2,718282

2,71611

2,955074

2,903202

3,00E+13

2,718282

2,71611

2,426668

2,609693

4,00E+13

2,718282

2,728199

2,677869

2,704075

5,00E+13

2,718282

2,71611

3,4256

2,903202

6,00E+13

2,718282

2,71611

2,426668

2,903202

7,00E+13

2,718282

2,704075

2,813059

2,704075

8,00E+13

2,718282

2,704075

1,482913

1,7655

9,00E+13

2,718282

2,71611

3,780207

3,592962

1,00E+14

2,718282

2,71611

1,63642

2,035095

2,00E+14

2,718282

2,777094

1

1

Примечание: жёлтым цветом выделены значения E > , красным цветом - значения E = 1, синим цветом - значения E < 2.

График 8.

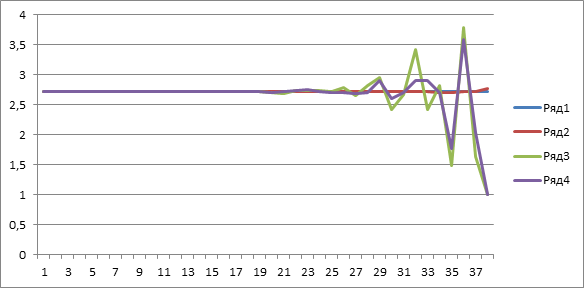
Таким образом, значения «числа» не равны общепринятому значению.

3.3. Проверка значений второго замечательного предела при помощи корней.

Выполним ещё одну проверку.

Так как второй замечательный предел: ,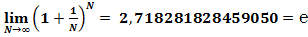

то 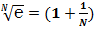, , 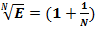при N → ∞, = E, соответственно, должно быть: .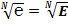

Вычислим значения E, , n√ E, n√ и значения n√ N при значениях N → ∞.

Результаты сведём в таблицу 7.

Таблица 7.

N

E = (1 + 1 / N) ^ N

n√ N

n√ E

n√

           

1

2

2,718281828

1

2

2,718281828

10

2,59374246

2,718281828

1,258925412

1,1

1,105170918

100

2,70481382

2,718281828

1,047128548

1,01

1,010050167

1000

2,716923932

2,718281828

1,006931669

1,00100000

1,00100050

10000

2,718145927

2,718281828

1,000921458

1,00010000

1,00010001

100000

2,718268237

2,718281828

1,000115136

1,00001000

1,00001000

1000000

2,718280469

2,718281828

1,000013816

1,00000100

1,00000100

10000000

2,718281694

2,718281828

1,000001612

1,00000010

1,00000010

100000000

2,718281786

2,718281828

1,000000184

1,00000001

1,00000001

1000000000

2,718282031

2,718281828

1,000000021

1,000000001

1,000000001

1E+10

2,718282053

2,718281828

1,0000000023

1

1

1E+11

2,718282053

2,718281828

1,0000000003

1

1

1E+12

2,718523496

2,718281828

1

1

1

1E+13

2,716110034

2,718281828

1

1

1

1E+14

2,716110034

2,718281828

1

1

1

1E+15

3,035035207

2,718281828

1

1

1

1E+16

1

2,718281828

1

1

1

1E+17

1

2,718281828

1

1

1
           

Примечание: жёлтым цветом выделены значения E > , синим цветом - значения n√ E, n√ N и n√ , при которых они равны 1, красным цветом – значения E = 1.

При всех N должно выполняться равенство: , однако уже при значениях N ≥ 10000000, равенство не выполняется.

Зато, при возведении n√ E в степень 1 / (n√ E -1) при N ≥ 10000000000 появляется число :

.

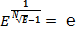Таблица 8.

N

1 / (n√ E -1)

E

(n√ E)^(N)

(n√ E)^(1 / (n√ E -1))
           

1

1

2,718281828

2

2

2

10

10

2,718281828

2,59374246

2,59374246

2,59374246

100

100

2,718281828

2,704813829

2,704813829

2,704813829

1000

1000

2,718281828

2,716923932

2,716923932

2,716923932

10000

10000

2,718281828

2,718145927

2,718145927

2,718145927

100000

100000

2,718281828

2,718268237

2,718268237

2,718268237

1000000

1000000

2,718281828

2,718280469

2,718280469

2,718280469

10000000

9999999,994

2,718281828

2,718281694

2,718281694

2,718281693

100000000

100000000,6

2,718281828

2,718281786

2,718281786

2,718281815

1000000000

999999917,3

2,718281828

2,718282031

2,718282031

2,718281827

10000000000

9999999173

2,718281828

2,718282053

2,718282053

2,718281828

1E+11

99999991726

2,718281828

2,718282053

2,718282053

2,718281828

1E+12

9,99911E+11

2,718281828

2,718523496

2,718523496

2,718281828

1E+13

1,0008E+13

2,718281828

2,716110034

2,716110034

2,718281828

1E+14

1,0008E+14

2,718281828

2,716110034

2,716110034

2,718281828

1E+15

#ДЕЛ/0!

2,718281828

3,035035207

3,035035207

#ДЕЛ/0!

Примечание: жёлтым цветом выделены значения E > , зелёным цветом – значения (n√ E) (1 / (n√ E -1)) равные , красным цветом значения 1 / (n√ E -1) не равные N.

Таким образом, члены последовательности E не равны , только при возведении их в степень 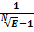, они становятся равными :

.

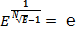3.4. Доказательство равенства значений второго замечательного предела единице.

Для доказательства равенства значений второго предела единице воспользуемся основами тригонометрической теории чисел или волновой арифметики.

Рассмотрим спираль Феодора Киренского в прямоугольной (декартовой) системе координат.

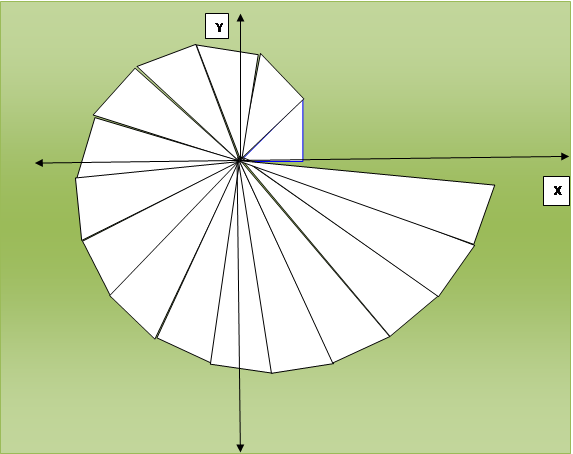
Рисунок № 1. Спираль Феодора Киренского.

Гипотенузы прямоугольных треугольников, из которых состоит спираль, равны квадратному корню из натуральных чисел от единицы до бесконечности, один из катетов всегда равен единице, второй катет последующего треугольника всегда является гипотенузой предыдущего треугольника.

Спираль Феодора Киренского наглядно показывает существование иррациональных чисел, квадратами которых являются натуральные числа, и трансцендентных чисел- углов в треугольниках, которые можно построить, но невозможно точно вычислить.

Спираль Феодора Киренского даёт возможность создать новый раздел математики – новую теорию чисел, тригонометрическую теорию чисел или волновую арифметику на основе элементарной арифметики, элементарной алгебры, геометрии и тригонометрии.

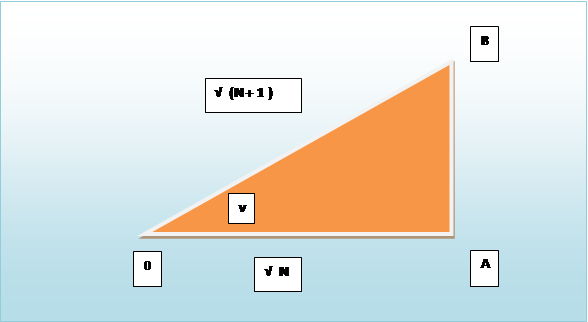
Рисунок 2. Треугольник.

Рассмотрим какой-либо прямоугольный треугольник (рисунок № 2) из спирали Феодора Киренского.

Будем считать, что катет AB равен 1.

Катет 0A равен √N, где N – числа натурального ряда.

На основании теоремы Пифагора гипотенуза 0B равна √(N + 1).

Угол, лежащий напротив катета AB, назовём углом ν (ню).

Тогда тангенс угла ν равняется: .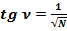

Синус угла ν равняется: .

Косинус угла ν равняется: .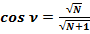

Если Ni – любое натуральное число, то на основании любого треугольника спирали Феодора Киренского получаются простые формулы – тригонометрические формулы чисел:

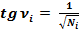
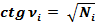
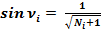
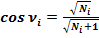(4)

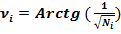; (5)

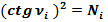, то есть квадрат котангенса угла νi равняется числу Ni .

И, наоборот, каждому числу Ni соответствует значение тригонометрической функции угла νi .

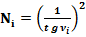
При N → ∞, угол ν → 0.

При N = 1, угол ν = π/4, или 45°.

При N → 0, угол ν → π/2, или 90°.

Формулу второго замечательного предела: 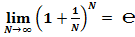, преобразуем согласно полученных формул:

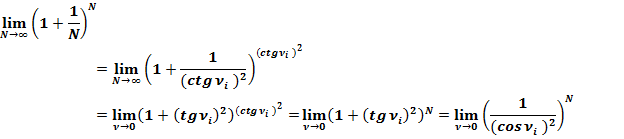
При N = 1, ν = π/4, значение второго замечательного предела равно:

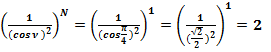
При N = ∞, ν = 0, значение второго замечательного предела равно:

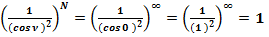, так как единица в любой степени, включая даже бесконечность, равна единице:

1∞ = 1*1*1*1*1*1*……….*1 = 1

Таким образом, предельное значение второго замечательного предела равно единице, а не числу .

4. Расчёт производных «числа» .

Классическое определение производной функции: производной функции y = f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

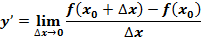
В нашем случае:

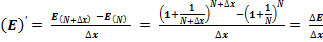
где N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, … , ∞.

ΔX = 0,1; 0,01; 0,001; 0,0001 и так далее.

Вычислим фактические значения производных.

4.1. Фактическое значение производных для ряда .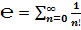

Ранее (таблица 1) было получено, что при числе N, равном 17:

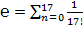= 2,718281828459050, то есть сумма ряда действительно стремится к предельному числу и имеет предел, который и называется числом .

Вычислять производные будем при N = 18.

ΔX будет принимать значения 0,1; 0,01; 0,001; 0,0001; 0,00001; 0,000001 и так далее.

Вычисления представим в таблице 9.

Таблица 9.

ΔX

Σ ряда

Δ = Σ -

′= Δ / ΔX

′/

′-

             
             

0,1

3,00416602

2,71828183

0,28588420

2,85884195

1,05170918

0,14056013

0,01

2,74560102

2,71828183

0,02731919

2,73191866

1,00501671

0,01363683

0,001

2,72100147

2,71828183

0,00271964

2,71964142

1,00050017

0,00135959

0,0001

2,71855367

2,71828183

0,00027184

2,71841775

1,00005000

0,00013592

0,00001

2,71830901

2,71828183

0,00002718

2,71829542

1,00000500

0,00001359

0,000001

2,71828455

2,71828183

0,00000272

2,71828319

1,00000050

0,00000136

0,0000001

2,71828210

2,71828183

0,00000027

2,71828196

1,00000005

0,00000013

0,00000001

2,71828195

2,71828183

0,00000012

11,71828177

4,31091495

8,99999994

1E-09

2,71828184

2,71828183

0,00000001

11,71828190

4,31091500

9,00000007

1E-10

2,71828183

2,71828183

0,00000000

11,71827968

4,31091418

8,99999785

1E-11

2,71828183

2,71828183

0,00000000

11,71822639

4,31089458

8,99994456

1E-12

2,71828183

2,71828183

0,00000000

11,71818198

4,31087824

8,99990015

Примечание: жёлтым цветом показаны значения производных функции ()′, которые гораздо больше .

Таким образом, при ΔX ≤ 0,00000001, производные ()′ перестают быть равными :

()′ = 11,71828177, вместо = 2,718281828459050,

()′/ = 4,31091495,

()′- = 8,99999994.

4.2. Фактическое значение производных для второго замечательного предела .

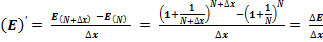
где N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, … , ∞.

ΔX = 0,1; 0,01; 0,001; 0,0001 и так далее.

Вычислим фактические значения производных.

Расчёты будем вести табличным способом.

Таблица 10.

N

ΔE / ΔX

ΔE / ΔX

ΔE / ΔX

ΔE /ΔX

ΔE / ΔX
 

ΔX = 0,1

ΔX = 0,01

ΔX = 0,001

ΔX = 0,0001

ΔX = 0,0001
           

1

0,36616559

0,384179427

0,386081788

0,386273093

0,386292234

2

0,156824369

0,161732014

0,162239867

0,162290829

0,162295927

3

0,08707761

0,089090977

0,089297466

0,089318167

0,089320238

4

0,055370689

0,056387515

0,05649126

0,056501656

0,056502695

5

0,038304702

0,038888417

0,03894777

0,038953715

0,03895431

6

0,028071216

0,028436864

0,028473954

0,028477668

0,028478039

7

0,021453687

0,021697729

0,02172244

0,021724914

0,021725161

8

0,016928591

0,017099516

0,017116798

0,017118528

0,017118701

9

0,013698135

0,013822473

0,013835031

0,013836288

0,013836414

10

0,011311575

0,011404834

0,011414245

0,011415186

0,01141528

20

0,003092532

0,003105836

0,003107172

0,003107306

0,003107319

30

0,001417506

0,001421631

0,001422045

0,001422087

0,001422089

40

0,0008099

0,000811681

0,000811859

0,000811877

0,00081188

50

0,000523251

0,000524176

0,000524268

0,000524278

0,000524279

60

0,000365672

0,000366213

0,000366267

0,000366272

0,000366272

70

0,000269876

0,000270219

0,000270253

0,000270257

0,000270259

80

0,000207329

0,000207559

0,000207582

0,000207585

0,000207587

90

0,00016425

0,000164413

0,000164429

0,000164431

0,00016443

100

0,000133325

0,000133444

0,000133456

0,000133458

0,000133459

200

3,36525E-05

3,36676E-05

3,36692E-05

3,367E-05

3,36819E-05

300

1,50047E-05

1,50092E-05

1,50097E-05

1,50095E-05

1,50076E-05

400

8,45373E-06

8,45562E-06

8,45588E-06

8,4559E-06

8,45422E-06

500

5,41561E-06

5,41659E-06

5,41685E-06

5,41847E-06

5,41918E-06

600

3,76326E-06

3,7638E-06

3,76387E-06

3,76225E-06

3,75837E-06

700

2,76611E-06

2,76649E-06

2,7667E-06

2,76981E-06

2,77263E-06

800

2,11853E-06

2,1188E-06

2,11861E-06

2,12049E-06

2,10627E-06

900

1,67435E-06

1,67455E-06

1,67471E-06

1,67373E-06

1,672E-06

1000

1,35652E-06

1,3567E-06

1,3568E-06

1,36291E-06

1,36366E-06

2000

3,39461E-07

3,3943E-07

3,39738E-07

3,37796E-07

3,24318E-07

3000

1,50912E-07

1,5086E-07

1,50088E-07

1,46239E-07

1,05027E-07

4000

8,49041E-08

8,48305E-08

8,45661E-08

7,16138E-08

1,29674E-08

5000

5,43504E-08

5,44087E-08

5,40754E-08

6,51879E-08

1,75326E-07

6000

3,77522E-08

3,76086E-08

3,69744E-08

3,11484E-08

-2,78E-08

7000

2,771E-08

2,76594E-08

2,50431E-08

3,61755E-08

1,46994E-07

8000

2,12604E-08

2,15711E-08

2,54619E-08

2,19647E-08

4,21085E-07

9000

1,6783E-08

1,66147E-08

1,8709E-08

3,66596E-08

2,15872E-07

10000

1,35698E-08

1,39551E-08

1,41087E-08

-4,88498E-09

2,87725E-07

20000

3,31586E-09

3,37392E-09

3,93552E-09

-3,12195E-09

-4,35918E-07

30000

1,50918E-09

9,37339E-10

-3,8507E-09

2,04281E-08

-4,61098E-07

40000

8,6867E-10

1,56728E-09

1,42819E-08

6,88516E-08

-1,0969E-07

50000

6,64122E-10

1,05476E-09

7,00995E-09

-2,40696E-08

-6,36602E-07

60000

2,7935E-10

1,77014E-10

-1,51967E-09

-3,44476E-07

-1,96332E-06

70000

3,34639E-10

6,52145E-10

7,5584E-09

-7,93143E-09

1,10467E-06

80000

1,59632E-10

7,34346E-10

-3,5536E-09

2,91527E-07

1,31091E-06

90000

3,52474E-11

-8,02958E-10

-9,48353E-09

-3,13607E-07

-3,35483E-06

100000

5,417E-11

-2,80642E-09

-4,37259E-08

-3,04512E-08

-3,5191E-06

200000

6,19194E-11

-8,16325E-10

-4,58744E-08

3,48548E-07

1,87841E-06

300000

-9,29878E-11

6,21379E-09

-3,17435E-09

-9,70601E-08

-1,00895E-05

400000

2,72522E-09

2,05583E-08

1,26445E-07

2,87532E-06

1,58783E-05

500000

-1,28112E-09

8,4007E-09

4,48508E-08

-1,94222E-07

9,48659E-06

600000

1,10401E-10

4,70233E-09

-1,66673E-07

1,01675E-06

5,608E-06

700000

6,74132E-10

-1,38041E-09

1,04821E-07

-1,00693E-07

6,29434E-06

800000

2,56363E-09

1,02327E-08

-5,7939E-08

2,64038E-06

-4,17679E-06

900000

5,64127E-11

-2,11742E-08

-2,33483E-07

-2,35658E-06

3,5735E-06

1000000

1,567E-09

-3,89342E-09

2,43289E-07

2,11154E-06

-3,34914E-06

2000000

-6,28731E-09

-1,02831E-07

1,81695E-08

2,10143E-08

-1,20221E-05

3000000

3,10543E-09

2,45352E-08

-6,66536E-07

3,28718E-06

2,4717E-05

4000000

7,87679E-09

-1,56861E-09

1,11114E-06

4,99523E-06

4,38362E-05

5000000

8,40266E-10

2,45923E-07

5,84226E-07

9,49347E-07

4,60054E-06

6000000

-1,35868E-08

1,32483E-07

8,68888E-07

4,61145E-06

4,20371E-05

7000000

1,00848E-09

-1,04802E-07

-3,17897E-07

-6,67391E-06

-7,0234E-05

8000000

1,5025E-08

4,72229E-07

1,66423E-06

1,35842E-05

0,000132784

9000000

-3,16037E-08

-3,1821E-07

-4,68166E-07

-7,39993E-06

-7,67176E-05

10000000

-2,84446E-08

-3,16581E-07

4,23537E-07

1,78892E-06

1,54428E-05

20000000

3,24128E-08

3,08061E-07

1,85738E-06

1,73506E-05

0,000172283

30000000

-8,41887E-08

1,53367E-07

7,18189E-07

6,36641E-06

6,28486E-05

40000000

-1,78705E-07

1,56558E-08

-4,55055E-07

-5,16216E-06

-5,22332E-05

50000000

-2,63782E-07

-1,09207E-07

-1,58136E-06

-1,63029E-05

-0,000163519

60000000

9,70494E-08

5,62752E-07

5,21978E-06

5,17901E-05

0,000517493

70000000

-4,51761E-07

-6,42046E-07

-6,76995E-06

-6,8049E-05

-0,000680839

80000000

-4,27909E-08

-7,33716E-07

-7,64296E-06

-7,67355E-05

-0,00076766

90000000

-7,19667E-08

-9,91495E-07

-1,01868E-05

-0,00010214

-0,001021668

100000000

1,46698E-07

1,22234E-06

1,19787E-05

0,000119543

0,001195183

200000000

2,01064E-07

1,88832E-06

1,87609E-05

0,000187486

0,00187474

300000000

1,1847E-07

1,10315E-06

1,09499E-05

0,000109418

0,001094095

400000000

2,28247E-07

2,22131E-06

2,21519E-05

0,000221458

0,002214518

500000000

2,03741E-07

1,98848E-06

1,98358E-05

0,000198309

0,001983045

600000000

1,36494E-07

1,32417E-06

1,32009E-05

0,000131968

0,001319641

700000000

9,16669E-08

8,8172E-07

8,78225E-06

8,77876E-05

0,000877841

800000000

2,41524E-07

2,38466E-06

2,3816E-05

0,00023813

0,002381266

900000000

2,69861E-07

2,67143E-06

2,66871E-05

0,000266844

0,002668411

1000000000

2,14689E-07

2,12242E-06

2,11998E-05

0,000211973

0,002119708

2000000000

2,20125E-07

2,18902E-06

2,1878E-05

0,000218768

0,002187663

3000000000

1,80733E-08

1,72578E-07

1,71762E-06

1,71681E-05

0,000171673

4000000000

2,22844E-07

2,22232E-06

2,22171E-05

0,000222165

0,002221641

5000000000

5,43658E-10

5,43654E-10

5,44009E-10

5,4623E-10

4,88498E-10

6000000000

4,53055E-10

4,5306E-10

4,53415E-10

4,52971E-10

4,44089E-10

7000000000

3,88329E-10

3,88356E-10

3,88578E-10

3,90799E-10

3,55271E-10

8000000000

3,39786E-10

3,39728E-10

3,39728E-10

3,37508E-10

0

9000000000

3,0203E-10

3,02025E-10

3,01537E-10

3,01981E-10

0

10000000000

2,71827E-10

2,71827E-10

2,71339E-10

2,70894E-10

0

20000000000

1,35914E-10

1,35936E-10

1,35891E-10

1,33227E-10

0

30000000000

9,06075E-11

9,05942E-11

9,05942E-11

8,88178E-11

0

40000000000

6,7959E-11

6,79901E-11

6,83897E-11

6,66134E-11

0

50000000000

5,43654E-11

5,43565E-11

5,41789E-11

5,32907E-11

0

60000000000

4,5306E-11

4,53415E-11

4,52971E-11

4,44089E-11

0

70000000000

3,88356E-11

3,88134E-11

3,95239E-11

4,44089E-11

0

80000000000

3,39773E-11

3,39284E-11

3,37508E-11

3,55271E-11

0

90000000000

3,02025E-11

3,01981E-11

3,01981E-11

0

0

1E+11

2,71827E-11

2,71339E-11

2,70894E-11

0

0

2E+11

1,35936E-11

1,36779E-11

1,42109E-11

0

0

3E+11

9,05942E-12

9,05942E-12

9,32587E-12

0

0

4E+11

6,79012E-12

6,79456E-12

6,66134E-12

0

0

5E+11

5,43121E-12

5,4623E-12

5,32907E-12

0

0

6E+11

4,53415E-12

4,52971E-12

4,88498E-12

0

0

7E+11

3,8769E-12

3,86358E-12

3,55271E-12

0

0

8E+11

3,39728E-12

3,41949E-12

0

0

0

9E+11

3,01981E-12

3,01981E-12

0

0

0

1E+12

2,71783E-12

2,75335E-12

0

0

0

2E+12

1,35891E-12

1,37668E-12

0

0

0

3E+12

9,10383E-13

9,32587E-13

0

0

0

4E+12

6,83897E-13

6,66134E-13

0

0

0

5E+12

5,41789E-13

5,32907E-13

0

0

0

6E+12

4,52971E-13

4,44089E-13

0

0

0

7E+12

3,86358E-13

3,9968E-13

0

0

0

8E+12

3,37508E-13

3,55271E-13

0

0

0

9E+12

2,9754E-13

0

0

0

0

1E+13

2,70894E-13

0

0

0

0

2E+13

1,37668E-13

0

0

0

0

3E+13

9,32587E-14

0

0

0

0

4E+13

7,54952E-14

0

0

0

0

5E+13

5,77316E-14

0

0

0

0

6E+13

4,44089E-14

0

0

0

0

7E+13

3,9968E-14

0

0

0

0

8E+13

0

0

0

0

0

9E+13

0

0

0

0

0

1E+14

0

0

0

0

0

2E+14

0

0

0

0

0

3E+14

0

0

0

0

0

4E+14

0

0

0

0

0

5E+14

0

0

0

0

0

6E+14

0

0

0

0

0

7E+14

0

0

0

0

0

8E+14

0

0

0

0

0

9E+14

0

0

0

0

0

1E+15

0

0

0

0

0

2E+15

0

0

0

0

0

3E+15

0

0

0

0

0

4E+15

0

0

0

0

0

5E+15

0

0

0

0

0

6E+15

0

0

0

0

0

7E+15

0

0

0

0

0

8E+15

0

0

0

0

0

9E+15

0

0

0

0

0

1E+16

0

0

0

0

0

2E+16

0

0

0

0

0

3E+16

0

0

0

0

0

4E+16

0

0

0

0

0

5E+16

0

0

0

0

0

6E+16

0

0

0

0

0

7E+16

0

0

0

0

0

8E+16

0

0

0

0

0

9E+16

0

0

0

0

0

1E+17

0

0

0

0

0

Таким образом, при увеличении N производная (E)’ стремится к нулю, кроме того, при уменьшении значений ΔX, нулевые значения производных (E)’ = 0 начинаются с меньших значений чисел N.

Данные таблицы 10 представлены на графике 9.

График 9.

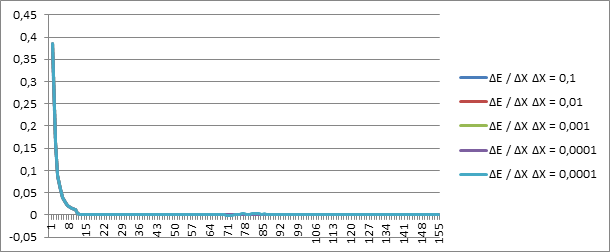
Для большей наглядности представлен график 9 на основании данных таблицы 7 при интервале чисел N от 104 до 108.

График 10.

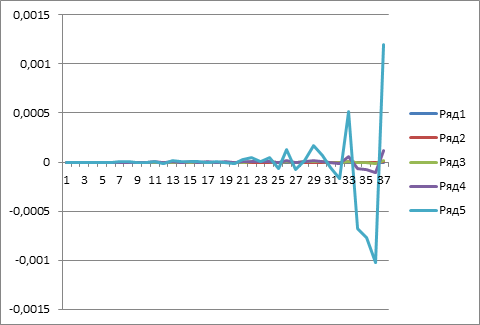
Вывод: таким образом, значения производной «числа»  при N → ∞ приближаются к нулю, а не к числу , что не соответствует общепринятому значению.

4.3. Доказательство общепринятого значения производной числа .

Докажем, что .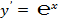

Считается, что .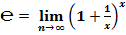

Придав приращение аргументу Δx, найдём приращение функции Δy:

.

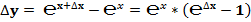Тогда, .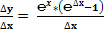

Таким образом, .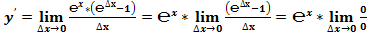

Чтобы раскрыть неопределённость , сделаем подстановку: ,

Тогда: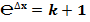

.

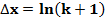
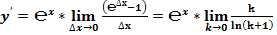Выполним вторую подстановку: 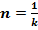, тогда 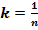, при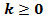 , n→∞ .

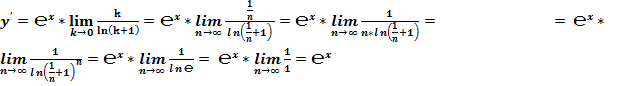, что и требовалось доказать.

Таким образом, доказано, что 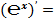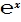, или производная функции равна самой функции.

4.4. Опровержение общепринятого значения производной числа .

1. Определим значение Δx, при котором .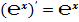

Имеем: производная функции равна самой функции:

.

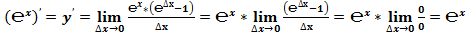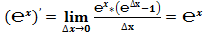, или .

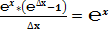Отсюда: 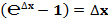, или .

Прологарифмируем выражение: ,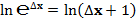

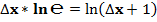, или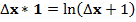

Таким образом, только при значении Δx = 0, 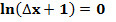, следовательно, только при

Δx = 0, производная .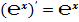

2. Будем считать, что:

.

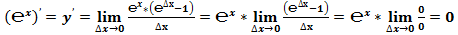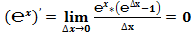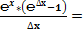, или 0.

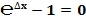Отсюда: , или , и .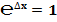

Прологарифмируем выражение: ,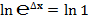

.

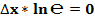Таким образом, только при значении Δx = 0, производная .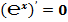

3. Будем считать, что:

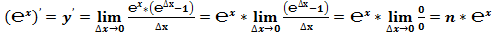, где

n – любое действительное число, кроме нуля.

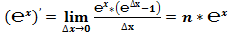, или .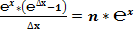

Отсюда: 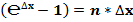, или .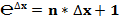

Прологарифмируем выражение: ,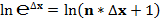

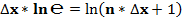, или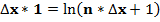

Таким образом, только при значении Δx = 0, 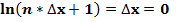, следовательно, только при Δx = 0 ,производная .

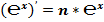4. Будем считать, что:

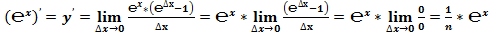, где

n – любое действительное число, кроме нуля.

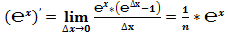, или .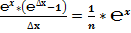

Отсюда: 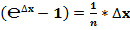, или .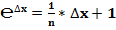

Прологарифмируем выражение: ,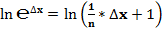

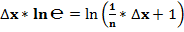, или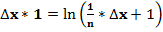

Таким образом, только при значении Δx = 0, 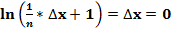, следовательно, только при Δx = 0 , производная .

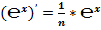Вывод: только при Δx = 0 , производная 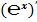может принимать любые значения, в том числе и 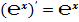, таким образом, решение не однозначно, а многозначно. При всех других значениях Δx .

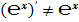4.5. Производные ряда .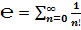

Определим производные для ряда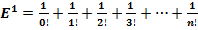

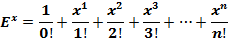
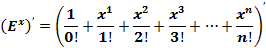
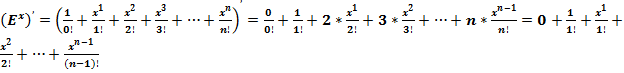
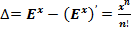
При x=1,

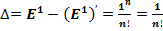
Δ =En+1 - En

Таблица 11.

N

1 / N!

E

ΔE

(E)’

Δ = E - (E)’
           

1

1

2

  

1

1

2

0,5

2,5

0,5

2

0,5

3

0,166666667

2,666666667

0,166666667

2,5

0,166666667

4

0,041666667

2,708333333

0,041666667

2,666666667

0,041666667

5

0,008333333

2,716666667

0,008333333

2,708333333

0,008333333

6

0,001388889

2,718055556

0,001388889

2,716666667

0,001388889

7

0,000198413

2,718253968

0,000198413

2,718055556

0,000198413

8

2,48016E-05

2,71827877

2,48016E-05

2,718253968

2,48016E-05

9

2,75573E-06

2,718281526

2,75573E-06

2,71827877

2,75573E-06

10

2,75573E-07

2,718281801

2,75573E-07

2,718281526

2,75573E-07

11

2,50521E-08

2,718281826

2,50521E-08

2,718281801

2,50521E-08

12

2,08768E-09

2,718281828

2,08768E-09

2,718281826

2,08768E-09

13

1,6059E-10

2,718281828

1,60591E-10

2,718281828

1,60591E-10

14

1,14707E-11

2,718281828

1,14708E-11

2,718281828

1,14708E-11

15

7,64716E-13

2,718281828

7,64722E-13

2,718281828

7,64722E-13

16

4,77948E-14

2,718281828

4,79616E-14

2,718281828

4,79616E-14

17

2,81146E-15

2,718281828

0

2,718281828

0

18

1,56192E-16

2,718281828

0

2,718281828

0

19

8,22064E-18

2,718281828

0

2,718281828

0

20

4,11032E-19

2,718281828

0

2,718281828

0

 

Таким образом: ,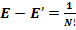

Соответственно, .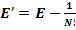

При значении N ≥17 (зависит от мощности компьютера) можно с достаточной степенью точности считать, E = , и равно производной ’, что соответствует общепринятому значению производной .

4.6. Производные второго замечательного предела: .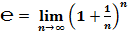

4.6.1. Основные понятия.

По правилу дифференцирования сложной функции найдём производную .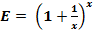

= = .

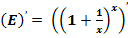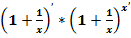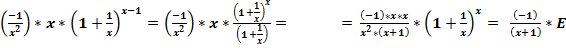Соответственно, ,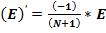

где N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, … , ∞

и .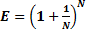

Таблица 12.

N

E

(E)’
       

1

2,718281828

2

-1

10

2,718281828

2,59374246

-0,235794769

100

2,718281828

2,704813829

-0,026780335

1000

2,718281828

2,716923932

-0,00271421

10000

2,718281828

2,718145927

-0,000271787

100000

2,718281828

2,718268237

-2,71824E-05

1000000

2,718281828

2,718280469

-2,71828E-06

10000000

2,718281828

2,718281694

-2,71828E-07

100000000

2,718281828

2,718281786

-2,71828E-08

1000000000

2,718281828

2,718282031

-2,71828E-09

10000000000

2,718281828

2,718282053

-2,71828E-10

1E+11

2,718281828

2,718282053

-2,71828E-11

1E+12

2,718281828

2,718523496

-2,71852E-12

1E+13

2,718281828

2,716110034

-2,71611E-13

1E+14

2,718281828

2,716110034

-2,71611E-14

1E+15

2,718281828

3,035035207

-3,03504E-15

1E+16

2,718281828

1

-1E-16

1E+17

2,718281828

1

-1E-17

Таким образом, с увеличением N производная (E)’ стремится к нулю.

Разложить в ряд функцию 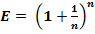можно двумя способами:

1. разложение в ряд Маклорена:

;

;

.

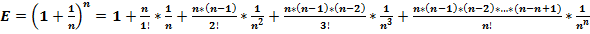
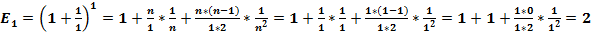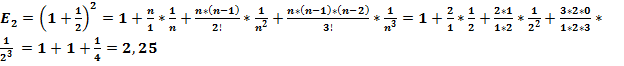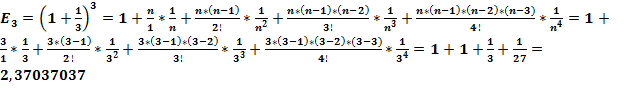2. по формуле бинома Ньютона (с применением коэффициентов треугольника Паскаля или биноминальных коэффицентов).

Треугольник Паскаля:

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 5 1

1 6 15 20 15 6 1

…………………………………………………………………………………………………

Биноминальные коэффициенты:

N

1

N

N*(N-1)/ 2!

N*(N-1)*(N-2)/ 3!

N*(N-1)*(N-2)*(N-3)/ 4!
           

1

1

1

0

0

0

2

1

2

1

0

0

3

1

3

3

1

0

4

1

4

6

4

1

5

1

5

10

10

5

6

1

6

15

20

15

7

1

7

21

35

35

8

1

8

28

56

70

9

1

9

36

84

126

10

1

10

45

120

210

;

;

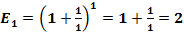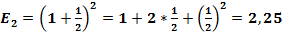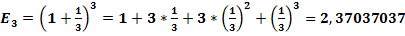, и так далее.

Так как члены рядов, составленного на основании бинома Ньютона равны, можно сделать предварительный вывод, что и производные будут равны.

Однако, производные, полученные на основании разложения бинома Ньютона в ряд Маклорена, будут значительно отличаться от производных, полученных на основании разложения бинома Ньютона с помощью биноминальных коэффициентов. Но так и должно быть, так как ряд Тейлора и ряд Маклорена основаны на коэффициентах, являющихся производными от биноминальных коэффициентов, при условии, что предел второго замечательного предела есть число .

4.6.2. Производные функции 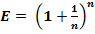при разложении с помощью биноминальных коэффициентов.

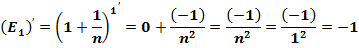
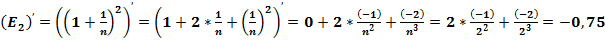
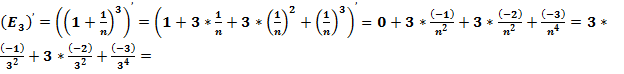- 0,592592593

Таким образом, при N = 1, ;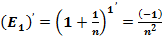

при N = 2, ;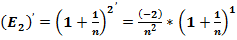

при N = 3, ;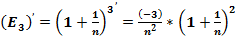

при N = n, 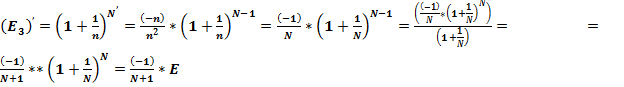, что соответствует общепринятой формуле производной функции по правилам дифференцирования.

Но полученные по формуле значения производной функции, не соответствуют фактическим значениям производных функции .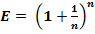

Фактические значения производных при N →∞ положительные и стремятся к нулю.

Полученные по формулам дифференцирования производные при N →∞ отрицательные и стремятся к нулю.

Таким образом, в любом случае производные функции второго замечательного предела не равны ни числу , ни производным числа .

4.6.3. Общие итоги по производным функций ряда 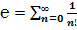и второго замечательного предела .

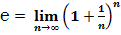1. Производные функций ряда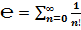

.

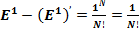
При N ≥ 17 , с большой степенью точности можно считать, что E = ,

(E)’ = ’ = , так как разница между функцией и её производной составляет всего: .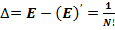

Однако, при ΔX → 0, как того требует само определение производной, при ΔX ≤ 0,00000001, фактические производные ()’ перестают быть равными :

()’ = 11,71828177, вместо = 2,718281828459050,

()’/ = 4,31091495,

()’- = 8,99999994.

Но это как раз и подтверждает ранее полученное решение о том, что производная 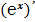может принимать любые значения.

2. Производные функций второго замечательного предела .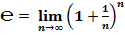

Но полученные по формуле: 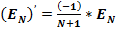, - значения производной функции, не соответствуют фактическим значениям производных функции .

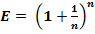Фактические значения производных при N → ∞ положительные и стремятся к нулю.

Полученные по формулам дифференцирования производные при N → ∞ отрицательные и стремятся к нулю.

Но в любом случае, при N → ∞, (EN)′ → 0, то есть (EN)′≠ .

5. Заключение.

Существует ли число ?

Да, число - существует.

Во-первых, как предел суммы ряда: .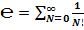

Во-вторых, как предел только некоторых чисел, то есть небольшого количества их, второго замечательного предела: 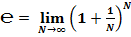, если эти числа образованы от числа 2 возведением в степень, при значении 5,6295E+14 ≤ N ≤ 9,0072E+15 , EN = = 2,718281828459050.

При значении N≥ 9,0072E+15, второй замечательный предел становится равным единице.

То есть предел второго замечательного предела при N → ∞ равен единице, а не числу .

Следовательно, ни о каком тождественном схождении указанных рядов не может быть и речи.

Общепринято и в любом курсе математического анализа доказывается, что функция x совпадает со своей производной (x)′: x = (x)′.

Но решение это не однозначно, а многозначно. И фактические вычисления производных даже суммы ряда: 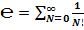при ΔX ≤ 0,00000001, - подтверждают не общепринятое значение: x = (x)′, а совершенно другое: x ≠ (x)′.

Значения производных, вычисленных на основе второго замечательного предела: 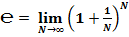, - при N → ∞ , стремятся к нулю: (EN)′ → 0, то есть (EN)′≠ .

Что опять подтверждает значительную разницу между рядам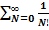и: и .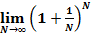

Таким образом, необходима ревизия многих разделов и приложений высшей математики, особенно, основанных на числе .