Великому Ньютону посвящается.
В статье содержатся результаты исследований автора по материалам его заявки на предполагаемое открытие «Закон спирального распределения плотности масс (зарядов) в поле центральной силы». Главный смысл заявки и результатов исследований: весь Мир от атомов до галактик и Вселенной построен по единому принципу и состоит из вихревых систем. В основе этого построения лежит закон тяготения Ньютона. Но закон Ньютона необоснованно назван законом всемирного тяготения, т.к. измерения постоянной тяготения производились только на Земле в лабораторных условиях и никто не доказал, что эта постоянная имеет одинаковое значение во всей Вселенной. Закон Ньютона должен быть расширен с учетом многомерности нашего Мира и он с полным правом будет называться Законом Всемирного Тяготения. ОТО в настоящее время остается главной теоретической базой при анализе почти всех современных космологических проблем. На базе уравнения советского ученого А.Фридмана создан не один десяток космологических моделей нестационарной Вселенной, из которых ни одна не является общепризнанной. Путем простых преобразований уравнение приводится к уравнению живых сил теории тяготения Ньютона, которое дает решения для круговых, эллиптических, параболических и гиперболических орбит (траекторий), т.е. дает стационарные и нестационарные решения. Таким образом, получается, что ОТО, которая приспособлена только для нестационарных объектов, является частным случаем теории тяготения Ньютона. Приведены новые законы небесной механики, дополняющие уравнения движения Кеплера и теорию тяготения Ньютона. Доказывается, что гравитационная постоянная не является одинаковой для всего материального мира и ее значение растет по направлению от Вселенной и галактик к атомному ядру. Заложена основа для объяснения природы сильных и слабых взаимодействий в атомах, а также для объединения всех взаимодействий и создания единой теории поля.
Введение.
На основе теории тяготения Эйнштейна (ОТО) разработаны десятки моделей Вселенной и все они нестационарные- расширяющиеся или пульсирующие. Ньютон, Кеплер, Галилей и другие их соратники не создавали десятки моделей Вселенной. Они просто открывали законы, которые в реальной Вселенной действуют, и проверяли их жизнью. Но теория тяготения Ньютона в начале двадцатого века прекратила развиваться, т.к. была подменена ОТО.
Цель исследования.
Целью исследования является обоснование высокой значимости законов Ньютона и Кеплера для объяснения явлений материального мира и открытия новых закономерностей его развития.
Материалы и методы исследования.
Количество гипотез и моделей, касающихся устройства нашей Вселенной продолжает расти. Авторы «Международного журнала прикладных и фундаментальных исследований» активно разрабатывают эту тематику. Среди многих авторов публикаций последних лет следует назвать фамилии, как Кричке В.О., Кричке О.А., Кричке В.В.[ 1], Сакуров В.Ф. [ 2 ], Пан В.Б.[ 3 ], Раджабов О.Р. [4 ], Задыхайло Д.К. [ 5 ], [ 6 ]. В работах авторов проработаны разные аспекты устройства Вселенной на всех уровнях материального мира, которые несомненно должны занять свое место в общей теории устройства Мироздания. Много открытий из области устройства Вселенной сделали советские ученые [ 7 ]. Цельная картина устройства Вселенной и нерешенные проблемы отражаются в энциклопедическом издании «Физика космоса»[8]
На основе изучения трудов известных ученых и популяризаторов науки в книгах, справочниках, журналах и газетах выявлены наиболее важные научные проблемы, которые до настоящего времени не решены методами исследований современной науки. С применением методологии научного познания, разработанной Ньютоном в его «Математических началах натуральной философии», проведен анализ выявленных проблем и определены возможные пути поиска их решения. Проведен поиск, найдены варианты решений, произведена их стыковка с существующими наблюдательными данными, полученными методами классической механики.
Результаты исследований и их обсуждение.
Известный советский и российский ученый, лауреат Нобелевской премии Л.В.Гинзбург в своей статье «К трехсотлетию «математических начал натуральной философии» Исаака Ньютона» [9] отметил, что И.Ньютон обобщил и существенно развил основные положения механики, созданные до него за предшествующие 2000 лет, а также наметил пути ее перспективного развития. Cам И.Ньютон об этом писал : « Если я видел дальше других, то потому, что стоял на плечах гигантов». Он имел ввиду в первую очередь Коперника, Галилея и Кеплера. Мы никогда не узнаем, почему И.Ньютон после математических начал отошел от научных исследований, но нет никаких сомнений, что если бы он этого не сделал, то довел бы теорию тяготения до такой стадии, которая не позволила бы объявить ее неспособной объяснить вековое смещение перигелия Меркурия и др.
Отодвинув на задний план теорию тяготения И.Ньютона, общая теория относительности тем самым отодвинула на задний план научные достижения ученых двух тысячелетий. Была прервана многовековая преемственность исследований.
Мировая научная общественность большие надежды питала на Большой Андронный Коллайдер в Европе, который должен был раскрыть многие тайны устройства материального мира. Однако, за десять лет работы он не принес никаких значимых результатов для раскрытия тайн строения Вселенной. Поэтому «поле жатвы» для любознательных исследователей продолжает оставаться большим.
Автор данной статьи твердо убежден: поскольку в обычной жизни главенствующее значение имеет преемственность поколений, так и в науке должна существовать преемственность теорий. Один даже самый гениальный ученый, вооруженный самыми современными инструментами исследований, не может увидеть мир во всем его многообразии, если не опирается на знания и опыт предшествующих исследователей. Результат неизбежно будет как в древней притче о трех слепых мудрецах, которые исследовали слона: один обследовал ногу и сказал, что слон – это колонна, другой о хоботе сказал, что слон - это пожарный рукав, а третий, держась за хвост, заявил, что слон – это веревка.
Не уподобилась ли наука этим трем мудрецам после утверждения общей теории относительности в качестве основной?
Автор считает, что каждый взгляд на мир для науки важен, должен быть оценен должным образом и включен в общее видение. Если бы палочки и колбочки человеческого глаза устраивали дискуссию по поводу того, какая из них правильнее видит, человечество до сих пор держалось бы за хвост слона и считало, что на нем держится мир.
Далее автор излагает свой взгляд на Мир , основанный на теории И.Ньютона, а, следовательно, и на знаниях минимум двух тысячелетий, т.е. на знаниях и опыте предков.
Наш Мир представляет собой суперпозицию из бесконечного множества миров и их свойств, вложенных друг в друга по принципу русской матрешки(Рис. 1)
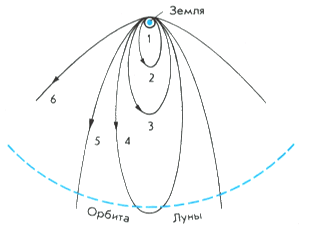
Рис. 1 Орбиты запуска спутников Земли.
Для наглядности рассмотрим виды орбит для запуска искусственных спутников Земли. Здесь изображены орбиты для запуска спутников с поверхности Земли: 1- круговая орбита, начальная скорость 7,9 км/с; 2,3,4 и др. – множество эллиптически орбит, начальная скорость от 8 км/с до 11.2 км/с; 5,6 и др. – множество параболических орбит, начальная скорость более 11.2 км/с. Орбита – это пространственная характеристика движения небесного тела. Поэтому особое внимание следует обратить на тот факт, что все они начинаются с одной общей (определяющей) точки, лежащей на поверхности Земли или близко от нее. Именно эта точка определяет, по какой траектории полетит спутник в межпланетном пространстве в зависимости от приданной ему скорости. Эта скорость зависит от расстояния точки от центра Земли и от массы Земли. Отвлечемся от конкретики и поместим в эту точку материальное тело, которое может мгновенно приобретать скорость от 0 до скорости света. При нулевой скорости тело будет падать к центру Земли с ускорением силы тяжести по отвесной траектории. При скорости света тело полетит по прямой, касательной к поверхности Земли. При других скоростях тело полетит по любой из траекторий, вид которых указан выше. Таким образом, само Пространство задает условия, которые необходимо выполнить, чтобы направить материальное тело по той орбите, которая нам требуется. В данном случае Пространство действует на материальное тело как силовое поле подобно действию магнита или проводника с током на железные опилки. Траектории движения в данном случае напоминают силовые магнитные или электрические линии. Но таких определяющих точек на поверхности Земли можно расположить бесконечное множество. Такое же бесконечное количество этих точек разместится на всех концентрических сферах вокруг Земли. Причем на каждой сфере определяющие точки будут задавать другие начальные скорости движения. В пространственном отображении это будет выглядеть как бесконечное множество торообразных поверхностей с круговыми, эллиптическими и параболическими образующими. И все эти поверхности являются силовыми. Так представляется система вложенных многомерных миров. Эту систему нельзя назвать иначе, как вихревой, и все законы, которые в ней действуют, должны исходить из законов вихря, о чем мы поговорим в последующих публикациях. Отметим только, что согласно описанной модели любая точка пространства характеризуется энергией, частотой и радиусом кривизны.
Во всех мирах действуют одни и те же законы. Главными законами, по которым космические объекты в определяющей точке и во всех точках силовых поверхностей распределяются по различным траекториям (орбитам), являются законы Ньютона и Кеплера, а также новые открытые и еще неоткрытые законы. Кеплер открыл законы движения небесных тел, а Ньютон открыл основные законы механики и подвел под законы Кеплера теоретические обоснования.
Первый закон Ньютона, закон инерции гласит – всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока и поскольку приложенные силы не заставят его изменить это состояние.
mv = const, где m - масса тела, v – скорость тела, mv - коли-
чество движения тела.
Второй закон – изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует: d/dt(mv) = F m a = F
Третий закон – действие всегда вызывает равное и противоположное противодействие:- d/dt ( m2v2 ) = - d/dt(m1v1 ) F2 = - F1.
Следует отметить, что Ньютон и Кеплер устанавливали свои закономерности для двухмерного пространства-времени, а система вложенных миров многомерна и законы эти потребуют совершенствования.
Для примера отметим второй закон Ньютона. В общем виде он будет выглядеть так: Fk = m ak / Rk-1, где
k - размерность пространства-времени;
F- силовой фактор пространства;
m – масса тела;
ak - ускорение.
При размерности k=1 закон принимает первоначальную форму, предложенную Ньютоном. При k=2 закон приобретает вид F2 = ma2/ R – момент силы. При k=3 F3 = ma3/ R2 - заряд ( об этом отдельный разговор). Таким вот образом все законы должны быть привязаны к многомерному Миру и тогда не будет нареканий типа «не смог объяснить вековое смещение перигелия Меркурия»).
Самым главным законом Ньютона является закон тяготения: каждые две частицы материи притягивают взаимно друг друга, или тяготеют друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними
F = Gm1m2/ r2
Ньютон определил следующие условия действия этого закона:
- если два притягивающихся тела имеют форму шаров и равномерную плотность, то они притягиваются так, как будто их массы сосредоточены в их центрах;
- так же притягиваются шаровые слои равномерной плотности, ограниченные двумя концентрическими шаровыми поверхностями;
- также притягиваются шары, плотность которых не везде одинакова, но вещество одинаковой плотности образует одинаковые слои.
По Ньютону во всех этих случаях размеры взаимодействующих тел должны быть исчезающе (т.е ничтожно, крайне, очень) малы по сравнению с взаимным расстоянием.
И вот здесь великий и во всем дотошный Ньютон допустил промах, из-за которого сто лет назад его теория тяготения была отодвинута на задний план после теории относительности.
Исчезающе–малый - это качественное определение, а для фундаментального закона этого мало. Нужны количественные критерии, которые никто за 300 лет так и не установил.
Во-первых, что считать размером тела, его радиус или диаметр, т.е. поперечник, как это теперь принято? Во-вторых, если одно тело исчезающее мало по сравнению с взаимным расстоянием ( например, Меркурий ), а другое (Солнце ) не очень, то как быть? Да и язык не поворачивается назвать исчезающе -малым наше Солнце, у которого есть еще солнечная корона, солнечный ветер и электромагнитное поле.
Если Солнце меньше взаимного расстояния с Меркурием примерно в 40 раз, то атомное ядро в атоме водорода меньше взаимного расстояния с электроном в 80000 раз, а ведь в атоме действует подобный закону тяготения закон обратных квадратов (закон Кулона). Достаточно ли 40 раз для Солнца?
О том, какие размеры тяготеющих тел допустимы в зависимости от взаимного расстояния, поговорим в одной из следующих статей.
Следовательно, закон тяготения Ньютона в применении к Меркурию требует поправок, о чем было заявлено еще во времена становления теории относительности. Если вычислить периметр (длину) эллиптической орбиты Меркурия с применением эллиптических интегралов и определить среднюю скорость Меркурия
по известному периоду обращения, то она оказывается меньше известной более, чем на 1%. Только этих факторов достаточно для необоснованности утверждения, что закон Ньютона не объясняет вековое смещение перигелия Меркурия на 43 угловые секунды. Да, в первоначальном виде не объяснял. Да и не должен был - ведь в нем до настоящего времени даже намека нет на наклон орбит и их прецессию, а также смещение восходящего узла. Эти все факторы отражают законы движения планет, которые Кеплер не открыл, которые в теории тяготения не используются, но которые есть и никуда от них не денешься:
- Квадраты периодов обращения перигелиев планет относятся друг к другу как пятые степени их средних расстояний от Солнца;
- Квадраты периодов прецессионного смещения долготы восходящего узла планет относятся друг к другу как седьмые степени их средних расстояний от Солнца;
- Циркуляция скорости каждой планеты при ее движении по орбите есть величина постоянная;
- Циркуляции скоростей планет относятся друг к другу как корни
второй степени из их средних расстояний от Солнца или по другому- квадраты циркуляции скоростей планет относятся одна к другой как их средние расстояния от Солнца;
- Квадраты секториальных скоростей планет относятся друг к другу как их средние расстояния от Солнца.
Необходимо отметить особое значение этих законов для совершенствования баллистических расчетов космических аппаратов. Это особенно важно в целях управления этими аппаратами в связи с направлением на создание групп малых космических аппаратов на невысоких орбитах. Баллистические расчеты, выполняемые методом итераций (последовательных приближений) требуют большой мощности вычислительных машин. Время расчетов начинает приближаться к времени прохождения управляющего сигнала до космического аппарата, что может повлиять на оперативность управления, вызвать сбои в управлении и сход аппаратов со своих орбит.
И это еще не все законы.
Для проверки законов, также как известных законов Кеплера, не требуются сложные расчеты и любой желающий, имеющий данные о движении планет, может проверить их путем простейших математических операций.
А что касается теории гравитации Эйнштейна (ОТО ), то в настоящее время для построения космологических моделей Вселенной наиболее широко применяется уравнение, полученное в 1922 г советским ученым Фридманом на основе ОТО. Из этого уравнения уже получено более двух десятков моделей Вселенной и все они дают расширяющуюся Вселенную. Рассмотрим это уравнение [ 7].
( dR/dt)² = 8/3 x πGR²ρ — k + 1/3 ΛR², где L - космологическая постоянная, учитывающая возможное существова-ние в мире дополнительной силы притяжения или отталкивания (кроме силы тяготения ).
k — постоянная, характеризующая тип модели Вселенной (k больше 0)- закрытая модель; k=0 – открытое евклидово пространство;(k<меньше 0) – открытое искривленное пространство.
R= R(t) — безразмерная функция времени- масштабный фактор, который связан с линейной координатой обекта r(t) (расстоянием от наблюдателя) соотношением r(t) = r?R(t), где r? — расстояние до объекта в настоящее время.
G – постоянная всемирного тяготения.
ρ — средняя плотность вещества во Вселенной.
Займемся преобразованиями .
Поскольку при решении уравнений теории относительности обычно переменным придают любые значения, необходимые для получения требуемого результата, мы имеем полное право поступать так же, но не причиняя вреда объективности.
Используя ( dR/dt)² = v2/ r02 и r = r? R можно записать
v2 = 8π/3 x GR²r02r + 1/3 ΛR² r02— kr r02 == r2/3( 8πGρ + Λ ) — kr02 = 1/3 r2 (8πGρ +8πGρ*) — kr02 == 4/3 πr3 (ρ + ρ* )2G — kr02 = 2GM*/r — kr02.
В формулах выше:
ρ* — плотность вещества в рассматриваемом объеме, вызывающая дополнительную силу притяжения или отталкивания;
М* - масса вещества в рассматриваемом объеме в момент времени t.
Поскольку k согласно уравнению Фридмана может принимать любые положительные и отрицательные значения примем K= 1/ r02. Тогда получим v2 = GM (2/ r — 1/ r0 )
В классической механике уравнение, которое мы получили путем простых преобразований уравнения Фридмана, называется уравнением энергии (уравнением живых сил ). Оно используется при решении задачи двух тяготеющих тел по законам Ньютона.
Полученный вывод дает основание утверждать, что не теория тяготения Ньютона является частным случаем теории относитель-ности Эйнштейна, а наоборот теория относительности является частным случаем теории тяготения Ньютона.
Уравнение живых сил в теории гравитации Ньютона дает как стацио-нарные, так и нестационарные решения и это соответствует структуре многомерного мира, описанной выше:
стационарные решения — это круговые и эллиптические замкнутые орбиты,
нестационарные решения- это параболические и гиперболические орбиты.
Но по теории тяготения Ньютона все эти решения привязаны к одной и той же точке поля гравитации центрального тела, а вид решения зависит от скорости тела в данной точке.
И мы с еще большим основанием можем утверждать, что теория относительности Эйнштейна является частным случаем теории гравитации Ньютона.
Описанными выше законами «небесный кодекс» не исчерпывается.
В него следовало бы включить диаграмму Герцшпрунга – Рассела (Рис.2), которая уже более 100 лет служит для классификации звезд по признакам температура поверхности – светимость.
Рис.2 Диаграмма Герцшпрунга – Рассела.
Это действительно важные характеристики, но не главные.
В небесной механике более часто и эффективно используются такие характеристики, как масса, плотность, диаметр, скорость осевого вращения, скорость орбитального движения, энергия и др.
Нельзя ли на базе этих характеристик установить закономерности для классификации всех небесных объектов, а не только звезд.
Оказывается, такие закономерности есть.
Обратим внимание на постоянную тяготения в теории относительности Эйнштейна (L) и ее связь с гравитационной постоянной (G).
L =kx,y,z,t/ ρx,y,z,t = 2G/ c4, где:
kx,y,z,t - кривизна пространства в точке А x,y,z в момент времени t.
ρx,y,z,t- плотность массы-энергии в той же точке в тот же момент времени t.
Из приведенного соотношения следует, что гравитационная постоянная пропорциональна кривизне пространства и обратно пропорциональна плотности массы-энергии.
Например, логарифмическая зависимость кривизны пространства, примыкающего к небесному телу(К ) и плотности этого тела (ρ) при
графическом построении в осях ?g К — ?g ρ дает семейства наклонных прямых, на которых каждый объект занимает свое место.
Для Солнечной системы все прямые параллельны, т.е. имеют одинаковый угол наклона, что говорит о постоянстве гравитационной постоянной в Солнечной системе.
Для уровней Вселенной, галактик и атомов прямые имеют разные углы наклона, что говорит о непостоянстве гравитационной постоянной во всем Мироздании.
Анализ динамики роста показателей кривизны пространства (диаметра объектов) и их плотности показывает: кривизна пространства от атомного ядра до Вселенной изменяется от 1020 м-2 до 10-52м-2, т.е. в 1072 раза, а плотность в 1055 раз – от 1014г/см3 до 10-31г/см3. Вследствие этого значение гравитационной постоянной должно уменьшаться по направлению от атомов до галактик и Вселенной. Если построить диаграмму кривизна – плотность в логарифмическом масштабе, то эта зависимость для каждого уровня будет выражаться наклонными прямыми линиями. Наклон линий разный и это свидетельствует о том, что гравитационная постоянная для каждого уровня имеет свое значение и эти ее значения изменяются дискретно.
Еще одна диаграмма- это диаграмма зависимости плотности объектов от логарифма циркуляции экваториальной скорости осевого вращения (ρ — ?g R²/Р). Эта диаграмма позволяет распределить объекты Солнечной системы по наклонным плавным кривым, подобно кривым на диаграмме Герцшпрунга – Рассела. При этом на диаграмме образуется несколько групп планет и их спутников:
1- большие планеты – Земля, Марс, Нептун, Уран, Сатурн;
2- малые планеты – Меркурий, Венера, Плутон;
3- спутники Юпитера – Ганимед, Каллисто, Титан, Тритон, Тетис, Диона, Рея, Энцелад и Мимас;
4- спутники Юпитера Европа и Ио, которые выделились на отдельную кривую и к ним присоединилась наша Луна.
И, наконец, самое удивительное : на этой диаграмме Юпитер находит-ся рядом с Солнцем почти в одной точке. Можно утверждать, что Юпитер является второй звездой Солнечной системы, формирующей свою планетную систему.
Если эту диаграмму построить в логарифмических показателях в осях ?g Г/Г0 — ?g ρ / ρ0 (Г/Г0 -отношение циркуляций экваториальной скорости небесного объекта и Солнца, ρ / ρ0- отношение плотностей небесного объекта и Солнца соответственно ), то на ней все звезды, планеты и спутники планет Солнечной системы размещаются на параллельных наклонных прямых, находящихся на одинаковом расстоянии друг от друга. При этом тангенс угла наклона к горизонтальной оси (ось ?g Г/Г0) равен 1,25 ± 0.077, что соответствует среднему углу 51,33°. При этом отношения логарифмов плотности и циркуляции квантуются согласно уравнению ?g ρ / ρ0=1,25 ?g Г/Г0+ 0, 33 n, где n=0, ±1, ±2, ±3….
Эта диаграмма имеет огромное предсказательное значение в космических исследованиях, т.к. позволяет определять гравитационную постоянную для исследуемых объектов, зная их осевое вращение и плотность. Здесь могут встретиться большие трудности, т.к. требуемые характеристики определены не прямыми измерениями а расчетным путем с использованием измеренного в лабораторных условиях значения гравитационной постоянной. Кстати результаты измерений гравитационной постоянной дают очень большой разброс результатов.Скорее всего происходит это из-за невыпол-нения условий Ньютона о симметричном распределении плотности, форме притягивающихся тел и соотношения размеров и расстояний.
К сожалению, объем статьи не позволяет привести здесь графически все диаграммы, но их на основе приведенных закономерностей может построить любой желающий, имеющий наблюдательные данные.
Заключение
В рамках небольшой статьи удалось сформулировать только некоторые общие закономерности нашей Вселенной и обосновать необходимость дальнейшего развития теории тяготения Ньютона.
На этом все новые закономерности не исчерпываются и будут описаны в последующих публикациях.
Все исследования проводились на основе большого количества наблюдательных данных, имеющихся в открытой печати. Конкретные практические приложения описанных и еще не описанных закономерностей требуют дальнейшего освещения и автор надеется, что будет предоставлена возможность выполнить это в последующих статьях.
