Введение. На современном уровне развития физики элементарными частицами называются частицы, которым нельзя приписать такой внутренней структуры, которая была бы простым соединением других частиц. В ряде случаев элементарные частицы рассматриваются бесструктурными, то есть материальными точками, обладающими определенными свойствами, фотоны в том числе.
Целью исследования является определение все же конкретной структуры, которой соответствует частица света – фотон, а также как эта частица функционирует. Дуализм или другими словами двойственность свойств этой частицы слабо объясняет, даже вносит неопределенность в ее функционирование. Конкретная структура многое бы прояснило и не только в ее свойствах, но и в других объектах материального мира, например, электронах, позитронах и прочих элементарных частицах, в которых фотоны или их части принимают участие в этих устройствах.
В данной работе методом математического анализа выводятся на основе некоторых предположений уравнения движений фотона, распределения его внутренней энергии, а результаты сравниваются с опытными данными уже полученными научными методами.
Итак, фотоны - это класс элементарных частиц, характеризующихся многими общими свойствами. Фотоны имеют нулевую массу покоя. Они, как полагают, являются квантами электромагнитного поля – бозонами. Однако есть другое мнение. Как будет видно из дальнейшего, каждый из фотонов содержит одинаковое количество некой нейтральной материи, которая только в сочетании с определенным количеством энергии начинает приобретать другие свойства, а именно электрический заряд и массу. Фотон под воздействием полученной энергии совершает три разных движения, а именно колебательное, вращательное и поступательное. Из известных в настоящее время частиц из этого семейства самые плотные и несущие максимальную энергию частицы - это гамма-фотоны, которые составляют гамма-излучение. Для гамма-фотона в принципе известны все необходимые параметры. Превращение двух гамма-фотонов в электрон и позитрон, а также наоборот, дает право считать, что гамма-фотон имеет максимальную массу во время колебаний, равную одной из этих частиц, а также и ее размер, то есть s=2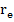 . Поскольку частота колебаний гамма-фотона также известна, гамма-фотон можно принять за базовый образец.
. Поскольку частота колебаний гамма-фотона также известна, гамма-фотон можно принять за базовый образец.
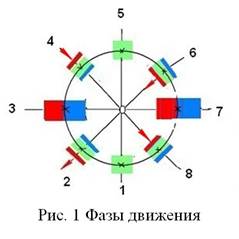
Рассмотрим совместное колебательное и вращательное движение фотона, так как разделить эти два движения сразу сложно. На рисунке 1 показаны положения слоев фотона через каждый поворот на сорок пять градусов. Крестиками показаны центр вращения фотона в каждой фазе. Колебания совершают только его слои. Один слой заряжен положительно (красный цвет), а другой отрицательно (синий цвет). Зеленым цветом окрашена нейтральная материя. Стрелками показаны, какие слои и в какую сторону двигаются. В первой фазе (1) материя фотона находится в нейтральном состоянии. Затем начинается растяжение (фаза 2). Положительно заряженный слой (красный) выходит из нейтральной материи (зеленого цвета) фотона. Тем самым обнажается отрицательно заряженный слой (синий). Полностью раздвинувшись (фаза 3), слои начинают опять надвигаться друг на друга, но теперь положительно заряженный слой двигается в обратном направлении (фаза 4). После того, когда слои полностью сдвинулись (фаза 5), начинается раздвижение слоев в противоположную сторону (фаза 6). Но фотон повернулся, и движение слоев происходит опять в прежнем направлении. В фазе 7 слои раздвинулись полностью, и начинается опять надвигание слоев друг на друга, и опять за счет перемещения положительно заряженного слоя (фаза 8). Таким образом, вернулись к фазе 1 - произошел полностью один такт колебания и один полный поворот фотона. При этом слои двигались в одном направлении, кроме фаз 4 и 8. У античастицы фотона двигается другой слой. Теперь, исходя из вышеописанного движения, рассмотрим отдельно колебательное движение слоев фотона. Фотон как частица из нейтрального вещества по форме является цилиндриком диаметром s и высотой также s. Колебания происходят вдоль оси цилиндрика (рис.2), гармонически изменяя длну s, а вращение происходит относительно оси y. Эта ось перпендикулярна направлению поступательного движения и перпендикулярна осевой линии цилиндрика.
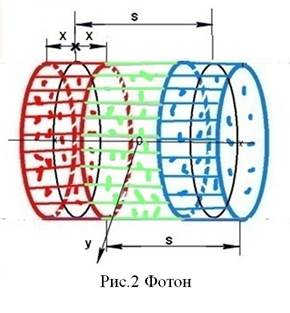
При колебательном процессе нейтральное вещество фотона, превысив длину s, разделилось на положительно заряженное и отрицательно заряженное. Нейтральное вещество фотона проявило свойство сегнетоэлектрика. Эти заряженные части вещества, или слои, раздвигаются в противоположные стороны на величину 2х. Заряды этих частей равны по своей величине и пропорциональны раздвинувшимся длинам. Заряженные части фотонного вещества несут заряды равные по абсолютной величине и разные по знаку q = 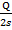 2x =
2x =  x, где Q полный заряд полностью разделенного вещества. Расстояние между заряженными центрами осталось равным s. Заряженные слои нейтрального вещества приобрели некую инерционную массу, равную
x, где Q полный заряд полностью разделенного вещества. Расстояние между заряженными центрами осталось равным s. Заряженные слои нейтрального вещества приобрели некую инерционную массу, равную 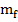 =
= 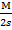 2x =
2x =  x , где M полная масса, входящая во все нейтральное вещество частицы, когда оно разделится полностью на два заряженных слоя. Величина
x , где M полная масса, входящая во все нейтральное вещество частицы, когда оно разделится полностью на два заряженных слоя. Величина 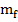 - это масса одного слоя.
- это масса одного слоя.
Квазиупругую силу, действующую между заряженными слоями, можно найти, используя закон Кулона: 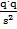 =
= 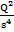 ·
·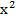 . Этот закон внутри нейтрального вещества не действует. Масса двигающегося слоя равна
. Этот закон внутри нейтрального вещества не действует. Масса двигающегося слоя равна 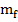 =
=  x. Уравнение колебания составит
x. Уравнение колебания составит  x
x 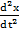 +
+ 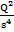
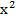 = 0. После преобразования оно предстанет в виде
= 0. После преобразования оно предстанет в виде 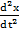 +
+ 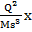 = 0. Это классическое уравнение механического колебания, но оно необычно с той точки зрения, что в нем изменяется масса и заряд вещества фотона - то есть, происходит преобразование вещества внутри фотона. Эти свойства начинают проявляться лишь после внесения порции энергии, переводящей нейтральную материю в другое состояние по аналогии со свойствами вещественной материи, которая может быть газообразной, жидкой и твердой. У нейтральной материи таких состояний столько, сколько существует частот колебаний у фотонов.
= 0. Это классическое уравнение механического колебания, но оно необычно с той точки зрения, что в нем изменяется масса и заряд вещества фотона - то есть, происходит преобразование вещества внутри фотона. Эти свойства начинают проявляться лишь после внесения порции энергии, переводящей нейтральную материю в другое состояние по аналогии со свойствами вещественной материи, которая может быть газообразной, жидкой и твердой. У нейтральной материи таких состояний столько, сколько существует частот колебаний у фотонов.
Уравнение колебаний показывает, что квадрат круговой частоты колебаний равен 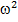 =
=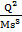 , а
, а 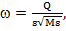 частота колебаний ν =
частота колебаний ν =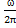 . Произошел процесс имитации волны.
. Произошел процесс имитации волны.
Уравнение колебаний фотона было выведено на основании общих предпосылок. Однако было введено несколько особых условий, можно даже сказать, спорных положений, поэтому проверим реальное отражение действительности составленного уравнения методом сравнения известных данных, полученных опытным путем, с теоретическим расчетом.
Один гамма-фотон, как было выяснено выше, должен обладать массой электрона или позитрона. Возьмем параметры электрона. Масса M = 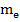 = 9,1091 · 10-28 г, заряд
= 9,1091 · 10-28 г, заряд 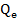 = 4,80298 · 10-28
= 4,80298 · 10-28 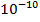 СГСЭ, радиус электрона
СГСЭ, радиус электрона 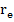 = 2,81777 · 10-13 см. Сопоставим соответствие истинного значения частоты гамма-фотона расчетному. Величину
= 2,81777 · 10-13 см. Сопоставим соответствие истинного значения частоты гамма-фотона расчетному. Величину 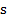 принимаем равной диаметру электрона
принимаем равной диаметру электрона 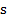 = 2
= 2 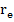 = 5,63554 · 10-13 см, величину Q =
= 5,63554 · 10-13 см, величину Q = 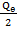 , как заряд одного слоя материи фотона, который совершает колебания. Таким образом, ν=
, как заряд одного слоя материи фотона, который совершает колебания. Таким образом, ν=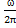 =
= 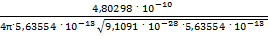 = 2
= 2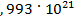 Гц. Вычисленная по формуле частота гамма-лучей соответствует определенному в науке значению. Из уравнения видно, что положительно и отрицательно заряженные массы фотона совершают перемещения. Величина перемещения заряженных слоев фотона определяется уравнением x =
Гц. Вычисленная по формуле частота гамма-лучей соответствует определенному в науке значению. Из уравнения видно, что положительно и отрицательно заряженные массы фотона совершают перемещения. Величина перемещения заряженных слоев фотона определяется уравнением x = 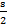 sin(
sin(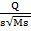 t +α), что следует из решения линейного дифференциального уравнения второго порядка колебаний слоев фотона, составленного ранее. Величина x это длина заряженного слоя, поэтому может принимать только положительные значения, то есть берется ее абсолютное значение. Начальная фаза в данном случае никакой роли не играет, поэтому α=0. Масса двух слоев фотона меняется по гармоническому закону
t +α), что следует из решения линейного дифференциального уравнения второго порядка колебаний слоев фотона, составленного ранее. Величина x это длина заряженного слоя, поэтому может принимать только положительные значения, то есть берется ее абсолютное значение. Начальная фаза в данном случае никакой роли не играет, поэтому α=0. Масса двух слоев фотона меняется по гармоническому закону 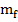 =
= 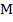 sin
sin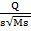 t или
t или 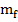 =
= 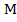 sin
sin .
.
Вычислим механическую энергию колебательного движения фотона. Она теоретически должна быть равна w = 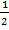
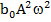 , где
, где 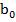 =
=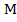 , A – амплитуда A =
, A – амплитуда A =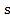 ,
, 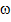 - круговая частота.
- круговая частота.
Таким образом, w = 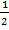
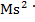
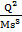 =
= 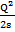 . Энергия колебаний гамма-фотона
. Энергия колебаний гамма-фотона 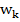 =
= 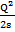 =
= 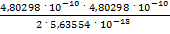 = 2,0467 · 10-7 эрг. Энергия, определенная по формуле Эйнштейна,
= 2,0467 · 10-7 эрг. Энергия, определенная по формуле Эйнштейна, 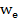 = m
= m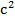 = 9,1091 ·10-28 · 2,9979 · 1010 · 2,9979 · 1010 = 8,1867 · 10-7 = 4
= 9,1091 ·10-28 · 2,9979 · 1010 · 2,9979 · 1010 = 8,1867 · 10-7 = 4 2.0467
2.0467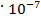 эрг. Это ровно в четыре раза больше. Энергия фотона, определенная с помощью постоянной Планка,
эрг. Это ровно в четыре раза больше. Энергия фотона, определенная с помощью постоянной Планка, 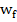 = hν, составит
= hν, составит 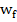 = hν = 6,625 · 10-29 2,993 ·1021 = 1,983 ·10-7 эрг. Эта величина немного меньше, но достаточно близка по значению, вычисленному по формуле механической энергии колебаний. Однако это энергия только одного движения фотона.
= hν = 6,625 · 10-29 2,993 ·1021 = 1,983 ·10-7 эрг. Эта величина немного меньше, но достаточно близка по значению, вычисленному по формуле механической энергии колебаний. Однако это энергия только одного движения фотона.
Чтобы узнать параметры фотонов с другой величиной энергии, примем параметры гамма-фотона как базовые, как это было раньше указано. Известно, что величина энергии фотона пропорциональна его частоте. Частота колебаний гамма-фотона 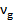 = 2
= 2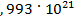 Гц. Так как
Гц. Так как 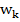 =
= 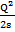 =
= 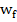 = hν, то
= hν, то 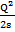 =
= 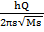 , а, следовательно,
, а, следовательно, 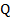 =
= 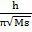 , поэтому ν =
, поэтому ν = 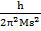 . Отсюда
. Отсюда 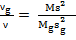 , где
, где 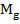 и
и 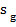 параметры гамма-фотона. Согласно формуле Эйнштейна энергия прямо пропорциональна массе, а масса частоте, поэтому
параметры гамма-фотона. Согласно формуле Эйнштейна энергия прямо пропорциональна массе, а масса частоте, поэтому 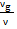 =
= 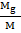 . Отсюда
. Отсюда 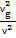 =
= 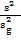 ,
, 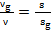 . Размер частицы с уменьшением частоты увеличился. Определим, как изменится заряд внутри фотона при изменении его частоты
. Размер частицы с уменьшением частоты увеличился. Определим, как изменится заряд внутри фотона при изменении его частоты 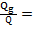
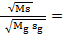 1. Заряд остался прежним, изменилась его удельная плотность по длине. Это означает, что все фотоны состоят из одинакового по размеру «куска» нейтральной материи, который в полной мере несет и одинаковый заряд. В итоге получаем
1. Заряд остался прежним, изменилась его удельная плотность по длине. Это означает, что все фотоны состоят из одинакового по размеру «куска» нейтральной материи, который в полной мере несет и одинаковый заряд. В итоге получаем 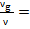
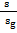 =
= 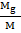 . Из этих соотношений можно сделать следующие заключения. Произведение массы на диаметр или длину цилиндра фотона величина постоянная
. Из этих соотношений можно сделать следующие заключения. Произведение массы на диаметр или длину цилиндра фотона величина постоянная 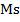 = const, произведение диаметра на величину энергии фотона также величина постоянная s
= const, произведение диаметра на величину энергии фотона также величина постоянная s w = const. Величина s это размер фотона по одной оси по оси цилиндра: по оси действия внутреннего давления, а величина w указывает на величину внутреннего давления фотона. Это соотношение является аналогом закона Бойля-Мариотта для идеальных газов и отвечает закономерностям кинетической теории газов. Кроме того величина
w = const. Величина s это размер фотона по одной оси по оси цилиндра: по оси действия внутреннего давления, а величина w указывает на величину внутреннего давления фотона. Это соотношение является аналогом закона Бойля-Мариотта для идеальных газов и отвечает закономерностям кинетической теории газов. Кроме того величина 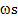 =
= 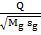 = const. Следовательно, параметры электрона являются ключевыми во всей серии фотонов. По ним и частоте колебаний определяются параметры всех фотонов.
= const. Следовательно, параметры электрона являются ключевыми во всей серии фотонов. По ним и частоте колебаний определяются параметры всех фотонов.
Если условно остановить колебания, фотон является цилиндриком высота и диаметр, то есть размер, которого по мере накопления энергии пропорционально уменьшается, а плотность увеличивается. Только добавленная порция энергии, увеличивающая частоту колебания на один герц, переводит материю в новое состояние: вещество фотона сжимается и внутренне разогревается, оно начинает быстрее двигаться – колебаться и вращаться. По величине частоты колебаний фотона или длины волны можно определить и другие его параметры. Так, например, если возьмем из всей гаммы фотонов, фотон красного света с длиной волны 7000 ангстрем, то он имеет расчетный диаметр 3,9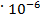 см или 390 ангстрем.
см или 390 ангстрем.
Как было ранее определено, фотон вращается в такт колебаниям, на что указывает и наличие у фотона спина. На вращение также должна затрачиваться энергия. Энергия вращения равна 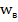 =
= 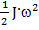 , где J – момент инерции, а
, где J – момент инерции, а 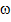 угловая скорость, численно равная круговой частоте. Момент инерции определим, применив схему, указанную на рисунке 2. Он равен J =
угловая скорость, численно равная круговой частоте. Момент инерции определим, применив схему, указанную на рисунке 2. Он равен J = 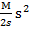 ∫
∫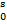 2dx =
2dx = 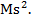 Отсюда получаем
Отсюда получаем 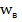 =
= 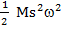 =
= 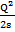 . Энергия равна энергии колебаний.
. Энергия равна энергии колебаний.
Материя фотона совершает относительное движение – это колебательное движение и переносное – это вращательное движение. Значит, к нему применима теорема Кориолиса. Колебательное движение выражается, как это следует из уравнения, x = 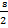 sin
sin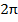 νt. Отсюда определим скорость относительного движения как производную по времени. Она будет равна
νt. Отсюда определим скорость относительного движения как производную по времени. Она будет равна 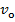 =
= 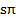 ν cos
ν cos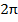 νt. Заменяем
νt. Заменяем 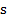 на его значение
на его значение 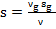 . Скорость вращения равна
. Скорость вращения равна 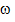 =
= 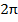 ν. Модуль ускорения Кориолиса при этом будет выражаться
ν. Модуль ускорения Кориолиса при этом будет выражаться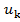 =2
=2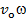 =4
=4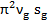 ν
ν cos
cos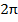 νt. Максимальная скорость поступательного движения фотона выразится, как интеграл в пределах одного такта колебаний, то есть
νt. Максимальная скорость поступательного движения фотона выразится, как интеграл в пределах одного такта колебаний, то есть 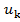 = ∫
= ∫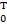 4
4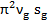 ν
ν cos(
cos(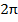 νt)dt. Вычислив его, получим скорость, равную
νt)dt. Вычислив его, получим скорость, равную 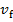 =8
=8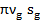 . Подставив значения, получим
. Подставив значения, получим 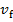 =4,2398
=4,2398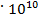 . Это амплитудное значение скорости. Чтобы получить среднее значение - действующее при синусоидальном колебании, амплитудное значение нужно поделить на
. Это амплитудное значение скорости. Чтобы получить среднее значение - действующее при синусоидальном колебании, амплитудное значение нужно поделить на 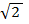 . Получаем среднюю скорость для всех фотона, равную
. Получаем среднюю скорость для всех фотона, равную 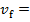 2,998
2,998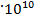 см/сек, то есть скорость света. Кинетическая энергия поступательного движения равна
см/сек, то есть скорость света. Кинетическая энергия поступательного движения равна 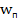 =
=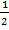 m
m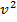 . Подставив значения, среднюю скорость то есть скорость света и максимальное значение массы получим еще половину энергии, имеющуюся у фотона, а просуммировав все составляющие энергии фотона, получаем, что формула Эйнштейна справедлива для определения полной энергии фотона, при условии, что фотон движется со скоростью света. Однако встает вопрос, почему взята средняя скорость, а масса максимальная? Поэтому сделаем для убедительности проверку на экстремум непосредственно подставив в уравнение
. Подставив значения, среднюю скорость то есть скорость света и максимальное значение массы получим еще половину энергии, имеющуюся у фотона, а просуммировав все составляющие энергии фотона, получаем, что формула Эйнштейна справедлива для определения полной энергии фотона, при условии, что фотон движется со скоростью света. Однако встает вопрос, почему взята средняя скорость, а масса максимальная? Поэтому сделаем для убедительности проверку на экстремум непосредственно подставив в уравнение 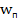 =
=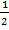 m
m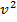 их значения в гармонической форме. Величина массы фотона равна
их значения в гармонической форме. Величина массы фотона равна 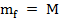 sin
sin , а величина скорости
, а величина скорости 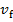 =8
=8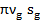 sin
sin , отсюда
, отсюда 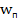 =32
=32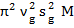 si
si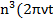 ). Экстремальное значение будет
). Экстремальное значение будет 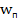 =32
=32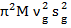 . То есть энергия поступательного движения равна
. То есть энергия поступательного движения равна 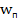 =
= 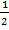 m
m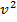 =
= 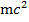 , так как амплитудное значение скорости
, так как амплитудное значение скорости 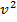 =2
=2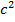 . Таким образом, формула Эйнштейна определяет энергию только поступательного движения фотона, то есть только часть его энергии. Это значит, что полная энергия фотона включая все виды затрат энергии на три типа движения при его разрушении будет выделена в размере
. Таким образом, формула Эйнштейна определяет энергию только поступательного движения фотона, то есть только часть его энергии. Это значит, что полная энергия фотона включая все виды затрат энергии на три типа движения при его разрушении будет выделена в размере 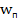 =
= 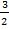 m
m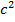 , что больше, определенной ранее.
, что больше, определенной ранее.
Скорость света в различной среде разная. Это зависит от тормозящего действия этой среды на летящую частицу, от лобового сопротивления. Величина энергии фотона от этого не зависит. Часть энергии фотон тратит на трение в этой среде, поэтому скорость его замедляется, но выйдя из нее, он восстанавливает свою скорость. Это как автомобиль, когда он едет по плохой дороге его скорость замедляется, хотя его мотор работает с прежней мощностью, выйдя на хорошую дорогу, его скорость увеличивается. Чтобы учесть воздействие среды, в науке введено понятие проницаемости ее, диэлектрической проницаемости, так как считается, что фотоны являются электромагнитными волнами. Взаимодействие зарядов фотона происходит внутри структуры фотона, поэтому диэлектрическая проницаемость внешней среды не оказывает воздействие на его заряды, а влияет тормозящее действие этой среды на движение фотона, как на частицу, то есть действие равно противодействию. Поэтому можно считать, что энергия поступательного движения затрачивается на преодоление сопротивления нейтральной материи, заполняющей все пространство. Если ускорение Кориолиса умножим на массу и получим силу этого сопротивления, а поделив на скорость и на величину лобовой площади фотона, то получим величину удельного сопротивления в зависимости от скорости движения. Размер лобовой площади ориентировочно будет равен ПЛ = 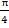
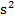 cos(
cos(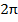 νt)+
νt)+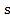 (
(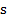 +
+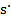 sin
sin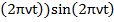 . Легко определить, что величина удельного сопротивления имеет относительно небольшую погрешность отклонения линейной зависимости от скорости движения фотона. Это значит, что фотон движется хотя и скачкообразно, но в ламинарном потоке, не образуя завихрений.
. Легко определить, что величина удельного сопротивления имеет относительно небольшую погрешность отклонения линейной зависимости от скорости движения фотона. Это значит, что фотон движется хотя и скачкообразно, но в ламинарном потоке, не образуя завихрений.
Скорость фотона за время одного такта колебаний изменяется от нуля до в 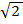 больше скорости «света», поэтому специальная теория относительности для него не применима.
больше скорости «света», поэтому специальная теория относительности для него не применима.
Скорость поступательного движения фотона определяется внутренней энергией самого фотона, которая тратится на преодоление сопротивления нейтральной материи, заполняющей пространство. Результаты исследования привели к следующим выводам:
1. Определена структура фотонов. Они не являются электромагнитными волнами. Это элементарные частицы, основу которых составляет «нейтральная» материя с внесенной в нее определенной порции энергии. Материя фотона совершает три вида движения: колебательное, вращательное и поступательное.
2. «Нейтральная» материя под воздействием колебательного процесса расщепляется на два электрически разнозаряженных слоя, приобретающих одновременно и свойства массы.
3. Масса фотона гармонически изменяется при колебательном движении.
4. Все фотоны содержат одинаковое количество «нейтральной» материи, но разное количество энергии.
5. Масса фотона зависит от удельной плотности заряда на единицу длины фотона.
6. «Нейтральная» материя фотона может иметь только кратное некоторой константе энергию, которая скачкообразно изменяет структуру этой материи: она ее уплотняет, увеличивается внутреннее давление, от чего увеличивается частота колебаний фотона.
Примечание. Все приведенные данные по элементарным частицам в данной статье находятся в открытом доступе, их можно найти в любом справочнике по физике, поэтому список литературы не приводится.
