Scientific journal

Scientific Review. Fundamental and Applied Research

Введение. 20 век подарил человечеству несколько математических теорий гравитации. Среди них - общая теория относительности (ОТО) А.Эйнштейна, которая объясняет сущность тяготения изменением геометрических свойств искривлённого четырёхмерного пространства-времени телами, имеющими массу. Экспериментальная проверка общей теории относительности была проведена на трёх эффектах: 1) искривление светового луча в поле тяготения Солнца; 2) смещение перигелия Меркурия; 3) гравитационное красное смещение. Проверка показала, что эти эффекты действительно существуют в масштабах Солнечной системы, и порядок их величин совпадает с предсказаниями.

Примерно в тоже время, Д.Уилер создал геометродинамику, - теорию гравитации, изучающую структуру пространства-времени в малых масштабах. Его исследования были посвящены эффектам квантования гравитации и гравитационному коллапсу. Теория предсказала существование во Вселенной нейтронных звёзд, имеющих в равновесных состояниях массу порядка солнечной, радиус от 10 до 20 км, период вращения 1 мс и температуру порядка 1010 К. Звёзды были обнаружены по периодическому излучению пульсаров, с которыми и были отождествлены.

Один из создателей матричной квантовой механики, В.Гейзенберг, в 50-х годах разрабатывает квантовую теорию гравитации для некоторой «экзотической Вселенной». В ней гравитационная постоянная, входящая в закон всемирного тяготения, проверенный экспериментально с высокой степенью точности, была «увеличена руками» более чем на 20 порядков. Только в такой «экзотической Вселенной» пространственные масштабы гравитационных кластеров становятся микроскопическими, а движение частиц в них квантуется.

В 70-х годах прошлого века американский исследователь К.Шоулдерс обнаружил в экспериментах новый физический объект - полый кластер одноимённых зарядов микронных размеров. Тогда у многих появился резонный вопрос: Какие силы могут компенсировать кулоновское взаимодействие, разрывающее скопление зарядов? Он повторяет извечный вопрос, существующий в ядерной физике более века: Чем скомпенсировано кулоновское взаимодействие зарядов в ядре любого атома? Стереотипный ответ со ссылкой на огромные ядерные силы с обменным взаимодействием, уже не устраивает современного исследователя по той причине, что (на наш взгляд) происхождение сил, удерживающих ядро, до сих пор остаётся неразгаданной загадкой.

В 80-м году Сарфатти (J.Sarfatti), продолжая исследования Гейзенберга, предположил, что зарядовый кластер могут удерживать «экзотические» гравитационные силы, возникающие при взаимодействии масс между двумя точечными зарядами.

Математическая модель Шоулдерса-Сарфатти, построенная на этом предположении, позволяет получить в сферическом случае распределение концентрации частиц-зарядов, захваченных такой квантовой гравитационной ловушкой. Она предсказывает микронные размеры зарядового кластера, количество зарядов в кластере, совпадающее с наблюдаемым, и такое распределение зарядов в кластере, которое формирует во внешней части «атмосферы» диффузную границу. Однако, существование такой «атмосферы» противоречит физическим свойствам зарядовых кластеров, обнаруженных экспериментально. Информация о зарядовых кластерах выставлена на сайте www.physics-evolution.ru. Там же есть полные тексты ссылок [1] и [6] этой статьи.

Исследования Шоулдерса показали, что у электронного зарядового кластера на внешней поверхности концентрация зарядов исключительно большая и превышает среднюю концентрацию электронов в твёрдом теле. Этот экспериментальный факт укрепляет уверенность в том, что скопления зарядов, описываемые моделью Сарфатти-Шоулдерса, не существуют в наблюдаемых границах нашей части Вселенной. Альтернативная теория зарядовых кластеров, удерживаемых градиентом давления самосогласованного поля, развита в [1] и согласуется с экспериментами Шоулдерса.

Релятивистская теория гравитации (РТГ), развитая А.Логуновым в 70-х годах, базируется на симметричном тензоре второго ранга, который, как утверждает автор, является реальным физическим полем, обладающим конечной плотностью энергии-импульса, ненулевой массой покоя и спиновыми состояниями 2 и 0. Гравитационные эффекты, рассчитанные для масштабов Солнечной системы в рамках РТГ, совпадают с предсказаниями общей теории относительности. Существенные различия, как в трактовке, так и в численных предсказаниях, обнаружены при обсуждении космологических моделей, следующих из теорий. Всё это напоминает приведённое выше совпадение/расхождение результатов, даваемых самосогласованной теорией кластеров одноимённых зарядов, экспериментов и теорией «экзотической гравитации» Гейзенберга-Сарфатти-Шоулдерса.

Противоречия, возникшие в конкурентных теориях, следует назвать кризисом математических идей гравитации искривлённого пространства, разрешения которого нам всем придётся ждать ещё очень долго. И сколько ещё математических идей 20 века, не выдержав детальной объективной экспериментальной проверки, попадут в пантеон неудачных теорий, покажет только время.

Уравнение, описывающее коллективное взаимодействие в гравитации, было угадано Р.Эмденом [2] в 1907 году задолго до понимания физики коллективных явлений, обнаруженных А. Власовым в 50-х годах [3]. К сожалению, Эмден не нашёл ни точных, ни приближённых аналитических решений, которые давали бы максимум плотности в центре шара.

Но отсутствие в любой теории точных или приближённых аналитических решений сразу же превращает её в «сундук» за семью печатями. Она не может дать важнейших дифференциальных параметров распределения: концентрации частиц, гравитационного потенциала, давления частиц, напряжённости поля. В ней нельзя определить масштабы физических величин, сопровождающих явление. То есть, в незаконченной теории нет результатов, по которым можно было бы производить сравнения с экспериментальными наблюдениями. С.Чандрасекар в [4] дал прозорливую оценку уравнению, полученному Эмденом, считая, что его можно применять и при анализе внутренней структуры строения звёзд.

Независимо от исследований Эмдена, по-видимому, даже ничего не зная о них, Я. Френкель построил в 1948 году систему трёхмерных векторных, а не тензорных, уравнений гравитации, которая описывает равновесные статические состояния частиц в самосогласованном поле [5]. Система, сведённая к уравнению относительно гравитационного потенциала, совпала со структурой уравнения Эмдена. Пытаясь найти распределение вещества в газовом шаре, он пришёл к неожиданному выводу о том, что полученное решение имеет особенность в нуле и приводит к результатам, лишённым физического смысла.

Одному из соавторов предлагаемой работы удалось понять причины неудач, возникших при построении самосогласованной теории гравитации газовых скоплений. Как показано в [6], при интегрировании уравнения Эмдена-Френкеля возникает математическая проблема выбора граничного условия (ГУ). Его корректный выбор не может быть произвольным потому, что он диктуется фундаментальным законом сохранения полного давления системы (гамильтоновой функцией).

Новый выбор ГУ показал, что газовые скопления, удерживаемые самосогласованным полем, имеют внутри себя полость, в которой вещество отсутствует. Оказалось, что это важное свойство, следующее из теории, совпало с многочисленными наблюдениями в астрономии.

В работе [6] продолжено исследование самосогласованной теории гравитации полых газовых шаров, предложенной Эмденом-Френкелем. В сферической симметрии найден класс приближённых решений для полевых ловушек первого рода, которые описывают распределение физических параметров в системах с потенциальной ямой. В них, для больших значений параметра состояния, поле выдавливает частицы в область с минимумом потенциальной энергии системы так, что внутри холодного кластера образуется полость. Силами, компенсирующими ньютоновское притяжение в газовых шарах, являются силы полевого происхождения. Они связанны с силой Бернулли, которая в кластерах взаимодействует с градиентом давления самосогласованного поля.

Цель исследования. В предлагаемой заметке найден класс точных решений, которые описывают распределение гравитационного потенциала в полевой ловушке второго рода. В ней самосогласованное поле выдавливает частицы в область бесконечно глубокой логарифмической щели, образованной потенциальной энергией системы. Численное моделирование указывает на возможность существования неоднородных скоплений нейтронов с температурой от 1011 до 1012 К, спектр масс которых можно идентифицировать со спектром масс объектов, обнаруженных в прошлом веке в центрах галактик и названных «сверхмассивные чёрные дыры».

Дифференциальное уравнение. Уравнение для гравитационного потенциала скопления j в сферической симметрии при одномерной зависимости имеет вид [6]

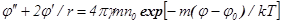, (1)

где 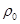- плотность частиц, 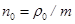- концентрация частиц системы на сфере 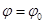, а штрихи означают дифференцирование по r. Его структура похожа на E-уравнение Эмдена [2].

Точное решение уравнения (1), найденное Френкелем в [5], имеет вид

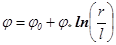, (2)

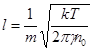где (3)

– пространственный масштаб, 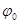- потенциал на сфере радиусом l, m - масса гравитирующей частицы, T - абсолютная температура, g - гравитационная постоянная, k - постоянная Больцмана, 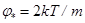- масштаб потенциала.

Как видно из (2), разность потенциалов и эквивалентная ей потенциальная энергия системы 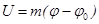имеют два знака. Они отрицательны для вещества, находящегося в области 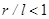, и положительны - для области 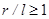. Распределение потенциальной энергии имеет две особые точк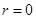и, и 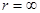, но не имеет привычного минимума.

Дифференциальные параметры полевой ловушки второго рода. Из (2) следуют основные физические характеристики полевой ловушки второго рода. Проекция r-й компоненты напряженности поля 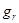имеет вид

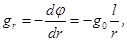(4)

где 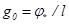- масштаб напряжённости поля. Напряжённость самосогласованного поля ловушки всегда направлена к центру системы и имеет в нуле особенность вида ~ -r-1.

Плотность, концентрация и давление частиц имеют распределение с особенностью ~ r-2 в нуле

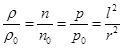. (5)

Как видно из (5), в ловушках второго рода поле выдавливает частицы в область бесконечно глубокой щели, образованной потенциальной энергией системы в начале координат.

Вещество кластера исчезает на бесконечно большом расстоянии от центра системы. Это указывает на принципиальное отличие состояний второго рода от состояний, исследованных ранее. Давление поля имеет особенность ~ r-2 в нуле

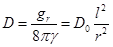, (6)

где 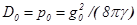- масштаб давления поля. Полное давление системы уже не является интегралом уравнения (1), поскольку оно изменяется по закону

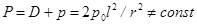. (7)

Градиент давления частиц, противоположный силе Бернулли, всегда направлен по напряжённости самосогласованного поля системы и имеет особенность вида ~ -r-3 в нуле

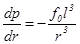, (8)

где 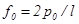- масштаб градиента давления.

Радиальная компонента градиента давления самосогласованного поля направлена против напряжённости и имеет особенность вида ~ r-3 в нуле

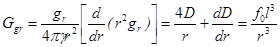. (9)

Из (8) и (9) видно, что дифференциальное условие равновесия произвольного элементарного объёма вещества в полевой ловушке второго рода

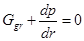(10)

выполнено во всех точках, кроме особых точек. Силы, удерживающие любой элементарный сферический слой вещества в равновесии, равны и противоположны друг другу. Поэтому систему, занимающую бесконечный объём, можно искусственно ограничить, выбрав радиус системы r1, внутри которого вещество отсутствует (радиус полости) и внешний радиус системы, за которым вещество также отсутствует, - r2.

Интегральные параметры полевой ловушки второго рода. Из (5) рассчитаем число частиц, удерживаемое кластером

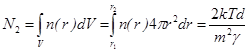, (11)

где 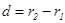- толщина слоя, занятого частицами. Из (11) видно, что чем меньше масса гравитирующей частицы, тем большее число частиц удерживается полем полого кластера при прочих равных условиях. Аддитивная масса кластера получается из (11)

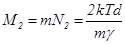. (12)

Она растёт с ростом температуры, толщины слоя и оказывается тем больше, чем меньше масса гравитирующей частицы.

Энергия самосогласованного поля в слое, занятом частицами, конечна и определяется из соотношения

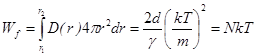. (13)

Её значение, с точностью до постоянной величины, совпадает с тепловой энергией частиц всего кластера.

Энергию взаимодействия частиц с полем (энергию связи) находим после интегрирования

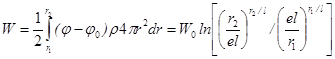, (14)

где 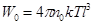- масштаб энергии связи. Как видно из (14), при 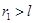энергия связи принимает положительные значения, а при 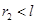- отрицательные.

Исследуем свойства подобия полевых ловушек, состоящих из гравитирующих частиц с одинаковой массой. Представим пространственный масштаб длины (3) в виде

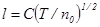, (15)

где 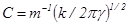=const1. (16)

Введём масштаб массы полевой ловушки второго рода

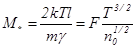, (17)

где 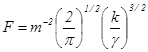=const2. (18)

Исключая из (15) и (17) концентрацию, придём к линейной связи между масштабом массы и пространственным масштабом при заданном значении температуры T:

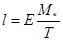, (19)

где E=C/F=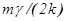= const3.

Из (19) следуют законы подобия:

a) в системах, имеющих одинаковую температуру, отношение масштаба массы к масштабу длины одинаково, а стало быть, чем больше масштаб массы кластера, тем больше его масштаб длины; обратное также верно.

b) в системах с одинаковыми масштабами масс объектов более горячий объект имеет меньший пространственный масштаб; обратное также верно.

c) объекты с одинаковым пространственным масштабом имеют одинаковое соотношение масштаба массы к температуре.

Исключая из (15) и (17) температуру объекта, получим, что масштаб массы полевой ловушки второго рода всегда пропорционален масштабу числа частиц 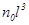в нем:

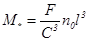. (20)

Масштаб массы M0 в полевых ловушках первого рода имеет вид

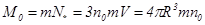, (21)

где R - радиус сферы нулевого давления поля, а N* - масштаб числа частиц в ловушке первого рода [6].

Найдём отношение этого масштаба к масштабу массы 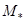ловушки второго рода

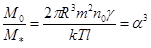, (22)

где 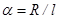- параметр состояния полевой ловушки первого рода [4]. Запишем массу ловушки первого рода с учётом (22)

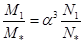, (23)

где N1 - число частиц. Из (23) видно, что полевые ловушки с потенциальной ямой обладают большей ёмкостью. Их масса может превышать масштаб массы на один-три порядка при изменении параметра состояния a в диапазоне 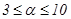, при прочих равных условиях.

Полевые ловушки с высокой температурой. Для полевой ловушки, удерживающей нейтроны, коэффициенты имеют следующие значения: С=1,0837×1019 (cм×K)-1/2; F=2,6785×1034 г×(cм×K)-3/2; E=4,0459×10-16cм×K/г. Из (17) следует, что для нейтронов, находящихся при температуре Т=1012К и изменении масштаба массы M* от 2×1039 г до 2×1042 г, пространственный масштаб l изменяется в пределах от 8×1011 cм до 8×1014 cм. Неравенства ограничивают интервал возможных изменений величины n0 в диапазоне от 1,8×1020 cм-3 до 1,8×1026 cм-3. Они далеки от средней ядерной плотности вещества. Соотношения подобия позволяют провести корректные вычисления.

В табл. 1 приведены зависимости масштабов полевых ловушек от n0 в предположении, что они состоят из нейтронов, нагретых до меньшей температуры T=1011 К (на порядок больше, чем в нейтронных звёздах [7]), а величина n0 может изменяться в диапазоне от 2,0×1020 cм-3 до 2,0×1026 cм-3.

Таблица 1. Масштабы полевых ловушек второго рода при температуре 1011 К.

В табл. 3 размещены результаты численного моделирования параметров сверхмассивных скоплений для ловушек первого и второго родов, находящихся при тех же условиях. Был принят следующий алгоритм моделирования:

1. По заданному n0 и Т=1011 K рассчитываем пространственный масштаб l.

2. Для заданного параметра состояния α определяем радиус R - сферы нулевого давления поля.

3. Для полевых ловушек первого рода обрываем распределение концентрации в точках, где 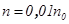и находим из численного моделирования приведённые значения полости r1/R и внешней границы r2/R, зависящие от параметра состояния α.

4. Вычисляем масштаб частиц в ловушках первого рода.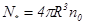

5. Из табл. 2 находим значения приведённого числа частиц 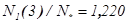при α=3 и 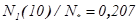при α=10.

Таблица 2. Приведённые значения полости и внешней границы полевой ловушки первого рода.

6. Рассчитываем аддитивную массу полевой ловушки первого рода из (23).

7. Для полевой ловушки второго рода считаем, что радиус её полости совпадает с r1, а её внешний радиус - с r2.

8. Число частиц и массу полевой ловушки второго рода находим из соотношений (11), (12).

В первую колонку табл. 3 заносим значение n0; во вторую – радиус полости; в третью – внешний радиус скопления; в четвёртую – число частиц в ловушке первого рода; в пятую – число частиц в ловушке второго рода; в шестую – массу скопления в ловушке первого рода, отнесённую к массе Солнца Ms=2×1033 г; а в седьмую – массу скопления в ловушке второго рода, отнесённую к массе Солнца Ms.

Таблица 3. Параметры сверхмассивных скоплений полевых ловушек первого и второго родов.

Из табл. 3 видно, что масса полевой ловушки первого рода больше, чем масса полевой ловушки второго рода при тех же параметрах. С ростом α это отличие возрастает. Причину этого объясняет соотношение (23). Масса полевой ловушки первого рода увеличивается с ростом параметра состояния α. При постоянном α увеличение концентрации n0 приводит к уменьшению массы ловушки и её геометрических размеров (см. 19). Обратное также верно.

Моделирование показывает, что увеличение температуры скопления на порядок (для тех же параметров состояния) приводит к увеличению массы полевых ловушек второго рода более чем на порядок. Диапазон их массы превышает диапазон масс полевых ловушек первого рода при исходной температуре с незначительным изменением геометрических размеров. Внешние размеры скоплений при нижних значениях n0 превышают средний радиус солнечной системы всего от 10-и до 18-ти раз. За средний радиус принято значение большей полуоси орбиты Плутона ~ 0,6×1015 см.

Заключение. Полевые гравитационные ловушки обладают свойством структурно-массовой независимости. В расчётах их структурным элементом был принят нейтрон. Если массу нейтрона заменить массой атома водорода для тех же температур, то скопление водорода будет иметь такие же размеры и массы. Замена водорода на гелий немного уменьшит масштаб массы скопления, но его можно увеличить за счет небольшого роста температуры.

Наблюдаемые «сверхмассивные чёрные дыры» в центрах галактик следует отнести к ранним очень горячим объектам, находящимся в состоянии высокотемпературной плазмы. Необходимо заметить, что астрономы до сих пор не пришли к единому названию указанных объектов. Так, первооткрыватель чёрных дыр Alan Dressler называет «Великой точкой притяжения (Great Attractor)» [8] похожие объекты, но с массой порядка 1014 солнечных масс. На наш взгляд, название «чёрная дыра» - неудачное. Находясь при температуре 1012 К, газовый шар будет ярче миллиона Солнц, и ему больше подходит термин «светлая дыра».

Для Great Attractor из нейтронов соотношение (12) даёт значение 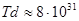см×К при 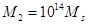. Из него следует существование двух возможных классов скоплений с одинаковой массой: низкотемпературные (при Т=1012 К имеют большую толщину слоя d~8×1019 см) и высокотемпературные (при Т=1014 К имеют толщину слоя, уменьшенную на два порядка). На наш взгляд, объекты Great Attractor с высокой температурой необходимо отнести к классу «сверхсветлых дыр».

Наблюдаемые массы сверхмассивных чёрных дыр могут отличаться от аддитивной массы. Здесь проявляют себя эффекты «избытка массы» и «дефекта массы», связанные со знаком энергии связи: 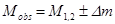, где 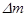– отличие наблюдаемой массы от аддитивной. В полевых ловушках первого рода преобладает эффект «избытка массы» из-за положительности энергии связи. В ловушках второго рода знак энергии связи может быть как положительным, так и отрицательным. Эффект «избытка массы» наблюдается в кластерах, полость которых имеет радиус 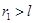, а «дефект массы» – в кластерах с отрицательной потенциальной энергией, внешний радиус которых 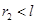. В зарядовых кластерах из протонов [9], с размерами ядра, будет наблюдаться «дефект массы», поскольку энергия взаимодействия протонов с полем отрицательна.

Оценка, проведённая для скопления нейтронов второго рода в первой строчке табл. 3 (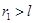), даёт значение эффекта «избытка массы» 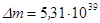г, которое составляет 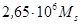, или 1,3% от аддитивной массы скопления. Это и есть «скрытая масса» чёрной дыры. Эффекты приращения масс чёрных дыр могут существенно изменять среднюю плотность массы во Вселенной.

Известный метод измерения массы чёрных дыр в центрах галактик по скорости близлежащих звёзд [10] не может ответить на вопрос о том, какой полевой ловушкой эти объекты удерживаются.

Если Солнце - газовый шар из гелия, то можно определить его температуру. При толщине слоя d, равной радиусу Солнца, из (12) следует, что средняя температура внутри Солнца достигает значения 46×106 К.

Из этого же соотношения следует независимое подтверждение возможности существования нейтронных звёзд без вращения, имеющих массу Солнца, диаметр 40 км и более высокую температуру 4×1011 К.

Из теории также следует, что Тунгусский феномен мог быть полым, рыхлым космическим «снежком» c массой в диапазоне от 4×1010 до 1,3×1012 тонн, состоящим из ледяных пылинок наноскопических диаметров [11]. Такой объект от 20 до 50 км в поперечнике мог быть заброшен на Землю ледяными гейзерами Энцелада – 61-го спутника Сатурна. Плотность потока частиц при падении такого «снежка» на землю будет существенно меньше в центре, чем в соседних слоях. Тогда в эпицентре падения производимые разрушения будут минимальны, что совпадает с наблюдениями Кулика в Тунгуске, в экспедиции 1921 года. Память о падении космического «снежка» до сих пор хранит не вываленный мачтовый лес, оставшийся в эпицентре падения.

На поверхности планет Солнечной системы и их спутников можно выделить класс кратеров определённой формы. В них есть валик вещества, выплавленный в виде кольца, и гладкая нетронутая текстура поверхности внутри и вне валика. В [6] получено распределение частиц вещества шара с полостью, налетающего на плоскую поверхность. Из распределения следует, что кольцевые кратеры могут оставлять газовые пузыри с радиусами порядка десятков-сотен километров. Полые плазмоиды с температурой ~ 104 К, способные оставлять такие следы, могут формироваться в потоках плазмы, забрасываемой на поверхность планет солнечным ветром.

Мы признательны академику Национальной Академии Наук Украины Барьяхтару В.Г. и хотим выразить благодарность за неподдельный интерес и моральную поддержку научного направления «Кластерные состояния газообразного вещества, удерживаемого самосогласованным полем».