Введение.
Полную энергию представляют в виде аддитивной суммы энергий различной природы, что противоречит принципам специальной теории относительности (СТО) и приводит к ложным выводам. Например, полагают, что масса электрона в атоме водорода увеличивается. Утверждение основано на СТО, но оно противоречит этой теории и эксперименту. Масса атома водорода в основном состоянии примерно на 13,6 эВ/с2 меньше суммы масс свободных электрона и протона, поэтому масса электрона в атоме уменьшается.
Цель исследования.
Цель работы заключается в исследовании нового закона сложения энергий - принципа суперпозиции энергетических состояний (ПСЭС) и возможности его применения в теории фундаментальных взаимодействий.
Принцип суперпозиции энергетический состояний (ПСЭС)
Энергию бесспинового электрона в атоме водорода представляют в виде суммы потенциальной и кинетической энергий. С точностью до членов второго порядка по 1/с в одночастичном приближении имеем (члены более высокого порядка далее учитывать не будем)
ε=mc2/(1-v2/c2)1/2-mc2+eφ = p2/2m -p4/8m3с2 +eφ. (1)
Здесь p=mv/(1-v2/c2)1/2- импульс, m, e=-[e], v – масса, заряд и скорость электрона, c – скорость света, φ –потенциал электрического поля протона (в общем случае ядра водородоподобного атома).
Из уравнения (1) следует, что при условии равенства скоростей кинетическая энергия связанного электрона совпадает с кинетической энергией свободного электрона. Справедливость этого положения вызывает сомнение. Полагают, что масса электрона, движущегося в атоме водорода, возрастает. Масса атома водорода в основном состоянии на 13,6 эВ/c2 меньше суммы масс свободных электрона и протона, поэтому масса электрона возрастать не может. За счет энергии связи масса электрона, согласно специальной теории относительности (СТО), уменьшается
mq=m+eφ/c2=m(1+eφ/mc2). (2)
Когда связанный электрон с массой (2) начинает двигаться, его масса увеличивается, но остается меньше массы покоя.
ε =mqvc2=mqс2/(1-v2/c2)1/2=mc2(1+eφ/mc2)/(1-v2/c2)1/2. (3)
Здесь mqv - масса электрона, движущегося в поле протона..Увеличение массы электрона за счет скорости с избытком компенсируется уменьшением массы за счет энергии связи (потенциальной энергии). Уравнение (3), в отличие от уравнения (1), соответствует принципам (СТО).
Аддитивное сложение энергий приводит к следствиям, противоречащим физическим законам. Электрон, находящийся одновременно в сильных электромагнитном и гравитационном полях может потерять массу, превышающую табличную. Дефект массы электрона в электрическом поле может составить eφ/mc2 =
-0,6 m
mq=m(1+eφ/mc2)=0.4m, (4)
Дефект массы в гравитационном взаимодействии по абсолютной величине может быть таким же
mg=m(1+U/mc2)=0,4m, (5)
где U- потенциальная энергия электрона в гравитационном поле.
При аддитивном сложении энергий для массы электрона имеем
mqg=m+eφ/c2+U/c2=-0.2m, (6)
что в принципе невозможно. Из ПСЭС имеем
mqg=m(1+eφ/mc2)(1+U/mc2)=0.16m (7)
Два взаимодействия вместе создают дефект массы 0.84 m. Взаимодействия оказываются взаимозависимыми. В рассматриваемом случае электромагнитное взаимодействие ослабляет гравитационное, а гравитационное - электромагнитное . Для полной энергии электрона в атоме водорода, находящемся в гравитационном поле, имеем
mqvgс2= mс2(1+eφ/mc2)(1+U/mc2)/(1-v2/c2)1/2 (8)
Для массы частицы, участвующей в n взаимодействиях, имеем
mn=mf1f2...fn. (9)
Функции fk (k=1,2,...n) определяют дефект массы в одном из взаимодействий, а их произведение суммарный дефект массы Уравнения (7-9) являются математической формулировкой ПСЭС, которому мы дали название по аналогии с принципом суперпозиции состояний квантовой механики.
Цель работы заключается в исследовании элементарных приложений ПСЭС к теории фундаментальных взаимодействий.
Тонкая структура энергетических уровней атома водорода.
В соответствии со СТО энергия электрона в атоме водорода
ε=(mqv-m)c2. (10)
Чтобы выразить энергию через импульс, умножим обе части уравнения (3) на с2 и возведем его в квадрат, имеем
mqv2c4-mqv2c2v2=m2c4(1+eφ/mc2)2. (11)
Найдем в явном виде mqvc2 и исключим энергию покоя mc2, имеем
ε=mqvc2-mc2=mc2[P02/m2c2+(1+eφ/mc2)2]1/2-mc2, (12)
где импульс
P0=mqvv=mv(1+eφ/mc2)/(1-v2/c2)1/2 (13)
В уравнениях (1,13) импульс определён в одночастичном приближении. В двухчастичном приближении необходимо учесть движение ядра относительно общего центра масс и дефект массы электрона, обусловленный электромагнитным взаимодействием. Кинетическая энергия ядра составляет доли процента от кинетической энергии электрона. Движение ядра учитывать не будем. Если рассматривать атом позитрония в одночастичном приближении, то ошибка составит 50%. Потенциальную энергию (дефект массы), как и кинетическую, следует разделить между электроном и протоном. Электрон и протон являются равноправными объектами электростатического взаимодействия, поэтому логично разделить дефект массы между ними поровну. Учет зависимости импульса ядра от потенциальной энергии даёт поправки примерно третьего порядка по 1/с, что соответствует сверхтонкой структуре, которая нас не интересует. Зависимость импульса электрона от потенциальной энергии следует уменьшить вдвое. Для реального импульса электрона имеем
P=mqvv=mv(1+eφ/2mc2)/(1-v2/c2)1/2. (14)
Уравнение для энергии (12) остается справедливым, так как потенциальная энергия не зависит от массы. Во втором приближении по 1/с имеем оператор полной энергии
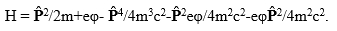(15)
Здесь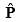 
оператор импульса. Появление двух последних членов в (15) свидетельствует о том, что полную энергию нельзя разделить на потенциальную и кинетическую. Кроме того, появляется магнитное поле с векторным потенциалом А=Pφ/mс, что является вполне естественным, так как движущийся электрон создает орбитальный магнитный момент.
Рассмотрим кратко существующие теории тонкой структуры, следуя [1]. Первая теория тонкой структуры была создана Зоммерфельдом в рамках квантовой теории Бора. Теория Зоммерфельда дает поправку на энергию уровней, согласующуюся с экспериментом
Δε=((mc2α4)/2n3)[3/4n-1/nφ], (16)
но с физической точки зрения она не верна, так как не учитывает спин - орбитальное взаимодействие. В (18) α – постоянная тонкой структуры, n-главное квантовое число, nφ-азимутальное.
Впервые спин-орбитальное взаимодействие было учтено Паули, который ввел понятие спина и матричный вектор-оператор σ, для которого справедливо соотношение
(σа)(σb)=ab+iσ[аb[, (17)
где a, b – произвольные векторы.
Он выразил в уравнении (1) импульс р через обобщенный импульс
р =(Pоб-eА/с). (18)
Так как операторы 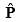об и А не коммутируют, их векторное произведение не обращается в нуль. Вводя оператор σ из (17-18) имеем
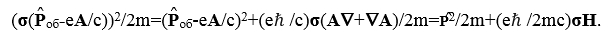(19)
Здесь H=rotA=(А∇+∇А) -магнитное поле,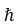 
- постоянная Планка - Дирака. Последний член в (19) представляет собой поправку на энергию спин-орбитального взаимодействия. Эта поправка оказалась вдвое больше той, которая необходима для получения поправки на энергию
Δε=(mc2α4/2n3)[3/4n-1/(j+1/2)], (20)
совпадающей с формулой Зоммерфельда (16), так как значения nφ и (j+1/2) равны (j-полный момент импульса электрона). Кроме того, введение обобщенного импульса в гамильтониан, в который он не входит, является искусственным приемом.
В настоящее время общепризнанной является теория тонкой структуры Дирака. Во втором приближении по 1/с гамильтониан в теории Дирака для двухкомпонентной волновой функции Шредингера имеет вид [1]
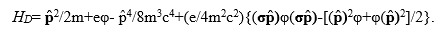(21)
Это уравнение дает поправку на энергию уровней, совпадающую с (20). Мы не будем вычислять средние значения физических величин в (21), они приведены в монографии [1].
Полученное нами уравнение (15) при учете зависимости импульса от потенциальной энергии позволяет получить гамильтониан Дирака
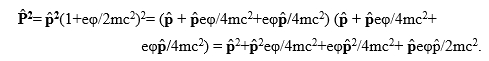(22)
Подставив (22) в (15) и, заменив оператор 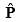произведением операторов σ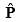, получим уравнение Дирака (21).
Предложенная нами теория тонкой структуры не претендует на замену теории Дирака, но она дает ясное физическое объяснение уменьшению поправки на энергию спин-орбитального взаимодействия вдвое по сравнению с теорией Паули. Это связано с зависимостью импульса электрона от потенциальной энергии. Если не учитывать эту зависимость, то можно получить уравнение Паули. Для этого необходимо учесть связь между векторным потенциалом магнитного поля и скалярным потенциалом электрического поля в уравнении (15) и ввести оператор σ.
Физический смысл теории Дирака не ясен даже специалистам. Так, Вейль полагал, что теория Дирака описывает атом позитрония [2]. В этом случае импульс взаимодействующих частиц уменьшается вдвое, что приводит к соответствующему уменьшению энергии спин-орбитального взаимодействия.
Применение ПСЭС в теории гравитации. Гравитационное красное смещение
Из общей теории относительности (ОТО) [3] для гравитационного красного смещения имеем
ν = ν0(1- 2GM/rc2)1/2 (23)
Здесь ν, ν0-частоты спектральных линий в гравитационном поле и вне поля.
В основе ОТО лежит принцип эквивалентности (ПЭ). По мнению авторов релятивистской теории гравитации (РТГ) [4] Эйнштейн не дал удовлетворительной формулировки ПЭ. Для точной формулировки принципа в ОТО мы не будем выписывать тензоры четвертого ранга римановой геометрии. Используем популярную формулировку: действие гравитационного поля эквивалентно действию ускорения. Ускорение никакого действия, кроме, силового, не оказывает. Гравитационное поле изменяет пространственно-временные соотношения. ПЭ ничего не дает для решения конкретных гравитационных задач. Для этого в ОТО используют ньютоново приближение. Полагают, что классический закон сохранения потенциальной и кинетической энергии в гравитационном поле выполняется точно
GMmg/r=mjv2/2. (24)
Здесь G-гравитационная постоянная, М-масса, mg-тяжёлая масса, mj- инертная масса.
Уравнение (24) является ещё одним постулатом ОТО. Из него следует, что теория тяготения Ньютона не верна. Так как правая часть уравнения (24) не является точным релятивистским значением кинетической энергии, левая часть не является точным значением потенциальной. Далее вступает в силу слабый принцип эквивалентности: тяжелая и инертная массы эквивалентны mg=mj. Затем в преобразования интервалов длины и времени СТО подставляют значение квадрата скорости из (24). Для интервалов длины и времени в гравитационном поле имеем
drg= drγ=dr (1- 2GM/rc2)1/2; dtg=dt/γ=dt/(1- 2GM/rc2)1/2. (25)
Длина отрезков и интервалы времени в гравитационном поле изменяются как в движущейся инерциальной системе отсчета. Так в теории появляется релятивистский множитель γ. Теперь ПЭ приобретает иной смысл: действие гравитационного поля в некоторой точке эквивалентно действию скорости, которую приобретает пробная частица, движущаяся из бесконечности с нулевой начальной скоростью в данной точке поля.
Подставляя в интервал СТО dr и dt из (25), получим интервал Шварцшильда вне сферически симметричного источника гравитационного поля в пустом пространстве, который лежит в основе вычислений гравитационных эффектов,
dSg2=- dr2g /(1- 2GM/rc2)+ dt2g(1- 2GM/rc2). (26)
Угловые координаты мы опустили, так как в этих направлениях длина отрезков не изменяется. Индекс "g" можно опустить, так как очевидно, что интервал относится к гравитационному полю. Если считать, что гравитационная статика Ньютона выполняется точно (сила и потенциальная энергия покоящейся частицы в теории Ньютона определены точно, поправки возникают в гравитационной динамике), из ПСЭС для интервала имеем
dSg2=- dr2g /(1- GM/rc2)2+ dt2g(1- GM/rc2)2. (27)
С точностью до членов второго порядка по 1/с интервалы (26, 27) совпадают.
Справедливость уравнений (26, 27) не очевидна. Геометрия пространства-времени определяется свойствами материи. Между изменением массы (энергии) и изменением интервалов длины и времени существует связь. В движущейся системе отсчета масса увеличивается, что приводит к уменьшению длины отрезков и замедлению скорости хода часов. В гравитационном поле островная масса уменьшается, что должно приводить к увеличению длины отрезков и ускорению хода часов. Это предположение может показаться ложным. Считают, что гравитационное красное смещение однозначно свидетельствует о замедлении скорости хода часов в гравитационном поле. В движущейся системе отсчета средняя частота источника света увеличивается, но это не говорит о том, что часы идут быстрее. Скорость хода часов определяется не частотой, а количеством излучаемых волн эталонными источниками (покоящимися и движущимися, находящимися в поле и вне поля) за единицу времени по часам наблюдателя.
Если реализуется интервал в гравитационном поле
dS2=- dr2 (1- GM/rc2)2+ dt2/(1- GM/rc2)2, (28)
то путешествия во времени отменяются. Часы в ракете, движущейся с ускорением, идут медленнее за счет увеличения скорости движения, но они во столько же раз идут быстрее за счет сил инерции, которые эквивалентны гравитационным.
Эйнштейн [5] считал, что наблюдатель в закрытом ящике (лифт Эйнштейна) не сможет установить находится ли он в инерциальной системе отсчета или свободно падает в гравитационном поле. Иначе говоря, система отсчета в таком лифте эквивалентна инерциальной. Но теория (ОТО) говорит об обратном: часы в лифте замедляют скорость хода, как вследствие увеличения скорости падения, так и вследствие уменьшения потенциала. В инерциальной системе отсчета часы идут с постоянной скоростью. В свободно падающем лифте масса и энергия частиц постоянна, происходит лишь превращение потенциальной энергии в кинетическую, поэтому частота эталонного источника постоянна. Согласно ОТО, длина лифта в радиальном направлении уменьшается по закону
L=L0(1-v2/c2)1/2(1-φg/c2)1/2. (28а)
Частота и длина волны источника в лифте остается постоянной и является эталоном длины, поэтому наблюдатель обнаружит, что длина лифта уменьшается со временем. В случае справедливости интервала (28) система отсчёта в свободно падающем лифте эквивалентна инерциальной.
Из ПСЭС для полной энергии частицы, движущейся в гравитационном поле, имеем уравнение, аналогичное уравнению (15)
ε = P2/2m+ mφg- P4/4m3с2-P2φg/4mc2- φgP2/4mc2.. (29)
Здесь φg - потенциал гравитационного поля. Если использовать ньютоново приближение (24), имеем
ε = mc2(1+2φg/c2)1/2/(1-v2/c2)1/2- mc2= P2/2m+ mφg- P4/4m3с2Pφg/4mc2- φgP2/4mc2- mφ2g/2c2. (30)
В уравнении (30) присутствует дополнительный член второго порядка по 1/с, что делает доступным экспериментальную проверку уравнений (29, 30). Потенциальная и кинетическая энергии симметрично входят в уравнение (30) вследствие симметричной зависимости массы от скорости и потенциала в ОТО.
В уравнениях (29,30) присутствуют перекрестные члены, которые можно представить в виде
P2φg/2mc2= PАg/2с (31)
где Аg= Pφg/2mc - векторный потенциал гравитационного поля, аналогичный магнитному. Уравнение (31) свидетельствует о появлении дополнительного взаимодействия между движущимися массами.
Из ПСЭС для гравитационного красного смещения имеем
hν = hν0(1- GM/rc2)= (P2/2m+eφ- P4/4m3с2- P2eφ/4m2c2-eφP2 /4m2c2)(1- GM/rc2) (32)
Вычисления в уравнении (8) можно проводить последовательно: сначала для двух взаимодействий, затем включать следующее.
ПСЭС позволяет установить, как влияет гравитационное поле на изменение потенциальной и кинетической энергий электрона. Гравитационное поле уменьшает кинетическую энергию электрона и увеличивает потенциальную. Увеличение потенциальной энергии с избытком компенсирует уменьшение кинетической, что приводит к красному смещению спектра.
При анализе космологического красного смещения не учитывают влияние гравитационного поля Метагалактики. Если она расширяется без образования новой массы и энергии, то ее потенциальная энергия увеличивается, что должно приводить к увеличению табличной массы элементарных частиц. Наблюдая космологическое красное смещение на расстоянии в миллиарды световых лет, не учитывают, что в то время масса частиц была меньше. Это само по себе дает дополнительное красное смещение, что эквивалентно ускорению расширения Метагалактики. Например, если Солнце "размазать" по всему пространству, его масса увеличится примерно на 2,2*1020кг. При этом увеличится масса электронов, а красное смещение исчезнет.
Космологическое красное смещение может быть объяснено в рамках модели статической Метагалактики. В этом случае оно является гравитационным, то есть не связано с расширением Метагалактики. Источник света всегда находится в центре Метагалактики. Это обусловлено конечной скоростью распространения сигнала. Фотон взаимодействует только с массой заключённой в сфере, которую он пролетел. Остальная Метагалактика за пределами этой сферы "не знает" о рождении фотона и не взаимодействует с ним. Масса вещества в сфере возрастает пропорционально кубу ее радиуса. На малых расстояниях красное смещение (ν0-ν)/ν0 увеличивается практически пропорционально квадрату расстояния до источника. На больших расстояниях необходимо учитывать дефект массы в сфере, обусловленный собственной гравитацией, что приводит к уменьшению зависимости красного смещения от расстояния. Зависимость (ν0-ν)/ν0 от расстояния имеет S - образный вид и стремится к единице на бесконечности.
Черные дыры
Рассмотрим два типа черных дыр: островные изолированные черные дыры (Ч1) и черные дыры в центрах скопления масс (Ч2). Существование изолированных островных черных дыр невозможно вследствие дефекта массы сжимающегося тела за счет собственной потенциальной энергии. Рассмотрим квазистатическое сжатие звезды массой М. Согласно ПСЭС, радиус черной дыры Rg=GM/c2. При сжатии до такого радиуса масса звезды уменьшается в два раза, и она не становится черной дырой
Мg=M(1-G Мg/rc2)=M/2 (33)
Здесь мы предположили, что вся потенциальная энергия излучается. В действительности часть потенциальной энергии переходит во внутреннюю энергию, но это не влияет на сделанный вывод, так как и в этом случае, оставшаяся масса меньше массы черной дыры. Многочисленные наблюдения сверхновых показывают, что они превращаются в нейтронные звезды, а не становятся черными дырами Ч1. Звезда "знает" сколько ей нужно сбросить массы, чтобы не стать черной дырой.
Черные дыры могут существовать только внутри пылевидного скопления масс (звезды здесь выступают в качестве пылинок). В центре такого однородного облака потенциальная энергия в полтора раза меньше чем на поверхности. Тело сначала необходимо удалить на поверхность, а затем на бесконечность. Это обстоятельство благоприятствует образованию черных дыр внутри таких объектов.
Определение: чёрная дыра Ч2 - это область пространства, в которой потенциальная энергия частицы по абсолютной величине равна её энергии покоя вне полей. ПСЭС дает условие образования черной дыры внутри галактик, скоплений галактик и в Метагалактике
Rпсэс =3GM/2c2. (34)
В ОТО для образования черной дыры внутри большого скопления масс условие еще более благоприятное (ОТО)
Rото =3GM/c2. (35)
Здесь R, M в (34, 35)-масса и радиус скопления масс, а не черной дыры.
При приближении к горизонту событий (сфере Шварцшильда) масса частиц и энергия связи их составляющих стремятся к нулю. В таких условиях атомы освобождаются от электронов, а их ядра распадаются. Ч2 окружена плазмой из элементарных частиц и квантов. Часть массы элементарных частиц обусловлена их зарядами (электрическими, лептонными, барионными) и спинами. Потеря этой массы ведет к исчезновению зарядов, то есть к нарушению законов их сохранения, поэтому они не могут проникнуть под сферу Шварцшильда. При расширении галактики черная дыра внутри неё уменьшается и может исчезнуть вследствие увеличения потенциальной энергии, а при сжатии - увеличивается. Черные дыры внутри скоплений масс находятся в стационарном состоянии и не могут поглотить объект, создающий их.
В РТГ [4] и в теории гравитации Фока [6] образование черных дыр невозможно. Авторы РТГ считают, что существование черных дыр противоречит принципу причинности. Из ПСЭС следует, что Ч2 ничего не поглощают и ничего не излучают, под сферой Шварцшильда нет материи, поэтому нет событий. Внутри Ч2 при минимально возможной потенциальной энергии потенциал гравитационного поля равен нулю, силы тяготения на сфере Шварцшильда и под ней отсутствуют, пространство-время плоское, а масса Ч2 равна нулю.
Заключение
Принцип суперпозиции энергий основан на специальной теории относительности. Для любого вида энергии справедлива формула Эйнштейна E=mc2. Если в результате некоторого взаимодействия масса частицы изменяется, то в другое взаимодействие частица вступает с этой изменённой массой. ПСЭС устанавливает взаимосвязь между различными взаимодействиями и может быть использован для построения теории комплексных (двух и более) взаимодействий. На основе ПСЭС построена теория тонкой структуры энергетических уровней водородоподобного атома, согласующаяся с экспериментальными данными и с теорией Дирака. Во втором приближении по 1/с гравитационное красное смещение совпадает с предсказанием ОТО, но ПСЭС дает более полное представление об эффекте. ПСЭС дает новое представление об образовании черных дыр и их свойствах.