Введение
Анализ кинетики разнообразных физико-химических процессов показывает, что в одних случаях идет прямое сложение скоростей, кинетических или энергетических характеристик, а в других – складываются их обратные величины.
В частности, такое предположение подтверждается формулой вероятности процесса переноса электрона 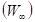 за счет перекрывания волновых функций 1 и 2 (в стационарном состоянии) при электронно-конформационных взаимодействиях [1]:
за счет перекрывания волновых функций 1 и 2 (в стационарном состоянии) при электронно-конформационных взаимодействиях [1]:
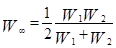 (1)
(1)
Уравнение (1) используется при оценке характеристик процессов диффузии, сопровождающейся безизлучательными переносами электронов в белках [1].
А так же: «Из классической механики известно, что относительное движение двух частиц с энергией взаимодействия U(r) происходит как движение материальной точки с приведенной массой 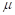 :
:
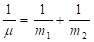 (2)
(2)
в поле центральной силы U(r), а общее поступательное движение – как свободное движение материальной точки с массой:
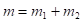 (3)
(3)
Такое положение вещей имеет место и в квантовой механике» [2].
Вместе с тем, остается нерешенной до конца проблема квантово-волнового дуализма, хотя применение уравнения де-Бройля позволяет определить границы проявления таких явлений. Но какое свойство при этом доминирует зависит от условий процесса. И определить заранее какая часть из них будет работать в каждом конкретном случае достаточно сложно, хотя известно, что волновая картина чаще имеет место при низких энергиях, а корпускулярная – при высоких.
Значительный интерес имеет и проблема многопланового проявления понятия энтропии. В теплофизических процессах энтропия (S) есть функция состояния системы, дифференциал которой в элементарном обратимом процессе равен отношению бесконечно малого количества теплоты, сообщенного системе, к ее абсолютной температуре:
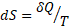 . (4)
. (4)
В статистической термодинамике энтропия изолированной и находящейся в равновесии системы равна логарифму вероятности нахождения ее в определенном макросостоянии:
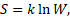 (5)
(5)
где W – число доступных состояний системы или степень вырождения микросостояний, k – постоянная Больцмана.
Поэтому применение и рассмотрение этих законов имеет многоплановые проявления, которые наиболее плодотворно используются статистической термодинамикой. Понятие энтропии, вытекающее из второго закона термодинамики, является критерием направленности процесса и степенью неупорядоченности систем.
Таким образом, эти проблемные вопросы физико-химии нуждаются в дальнейшем исследовании и обсуждении.
В данном исследовании делается попытка пояснения вышеуказанных проблем с позиции представлений о градиенте направленности физико-химических процессов при изменении их энтропийных составляющих.
1. Исходные данные
Был проведен [3] анализ характера изменения величины потенциальной энергии 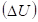 по ее знаку для различных потенциальных полей (таблица не приводится).
по ее знаку для различных потенциальных полей (таблица не приводится).
Получено, что значения –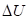 и соответственно
и соответственно 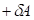 (положительная работа) соответствуют взаимодействиям, происходящим по градиенту потенциала, а +
(положительная работа) соответствуют взаимодействиям, происходящим по градиенту потенциала, а +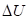 и
и 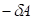 (отрицательная работа) имеют место при взаимодействиях против градиента потенциала.
(отрицательная работа) имеют место при взаимодействиях против градиента потенциала.
На основе анализа первого начала термодинамики было получено [3]:
1. В системах, в которых взаимодействие идет по градиенту потенциала (положительная работа) результирующая потенциальная энергия, как и приведенная масса, находятся по принципу сложения обратных значений соответствующих величин подсистем. Это – корпускулярный процесс, теоретической концепцией которого может являться энтропия.
2. В системах, в которых взаимодействие идет против градиента потенциала (отрицательная работа) выполняется алгебраическое сложение их масс и также соответствующих энергий подсистем. Это – волновой процесс, теоретической концепцией которого может являться негэнтропия.
3. Резонансное стационарное состояние систем выполняется при условии равенства степеней их корпускулярных и волновых взаимодействий. В термодинамике открытых систем продукция энтропии в стационарном состоянии полностью компенсируется потоком негэнтропии.
4. Все явления и процессы в природе и в Мире, включая человека, технику, экономику и экологию, идут только в двух энергетических направлениях. Или - по градиенту силового поля, с минимальной затратой энергии, или - против градиента, с максимальной затратой энергии. Первое направление соответствует понятию энтропия, а второе - понятию негэнтропия (отрицательная энтропия). В динамике процессов оба явления взаимосвязаны, и дополняют друг друга.
2. Энтропийные номограммы.
Для оценки структурных взаимодействий в простых и сложных системах классическая физика и квантовая механика широко используют кулоновские взаимодействия и их разновидности.
Так в [1] к электронно-конформационным взаимодействиям в биосистемах относят взаимодействия Ван-дер-Ваальса, ориентационные и заряд-дипольные взаимодействия. И как частный случай - обменно-резонансный перенос энергии. Но биологические и многие кластерные системы в структурной основе электронейтральные. И для них основное значение имеют равновесно-обменные энергетические взаимодействия не кулоновского типа, то есть это не зарядные электростатические процессы.
Идут структурные взаимодействия суммарных электронных плотностей валентных орбиталей соответствующих конформационных центров - процессы равновесного перетекания электронных плотностей за счет перекрывания их волновых функций. Чем ближе значения их энергетических характеристик, тем легче идет выравнивание электронных плотностей.
Еще Гейзенберг и Дирак [4] предложили обменный гамильтониан, выведенный в предположении о прямом перекрывании волновых функций взаимодействующих центров:
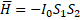 ,
,
где: 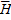 – спиновый оператор изотропного обменного взаимодействия для пары атомов,
– спиновый оператор изотропного обменного взаимодействия для пары атомов, 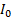 – постоянная обмена,
– постоянная обмена, 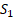 и
и 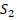 – интегралы перекрывания волновых функций.
– интегралы перекрывания волновых функций.
Каждая свободная атомная структура изначально имеет энтропийное равновесное состояние двух противоположных начал (орбиталь-ядро) в системе единой действительности (атом). В бинарной системе соответственно идут взаимодействия противоположных энтропийных составляющих от обоих атомов, пока не стабилизируется динамика энтропийного равновесия. Такие равновесно-обменные конформационные взаимодействия регулируют стабилизацию многих органических систем (кластеры, полипептидные цепи и т.д.). Поэтому, в данном подходе интегралы перекрывания волновых функций моделируются через величину относительной разности энергетических параметров взаимодействующих центров – коэффициент 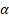 (в %) [5-6]. Такой параметр является прямой характеристикой степени энтропийного равновесия в системе. Исходные значения энергетических и размерных параметров для большинства элементов при разных валентно-активных орбиталях приведены в [3], и в других публикациях автора.
(в %) [5-6]. Такой параметр является прямой характеристикой степени энтропийного равновесия в системе. Исходные значения энергетических и размерных параметров для большинства элементов при разных валентно-активных орбиталях приведены в [3], и в других публикациях автора.
Применяя надёжные экспериментальные данные, получена номограмма зависимости степени структурных взаимодействий (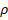 ) от коэффициента α, единая для широкого класса структур (рис. 1). В ней значения α от 0 до 5 соответствуют условиям энтропийного равновесия, при котором ρ=100%. Этот вид номограммы и ее зеркально-симметричный вариант (рис. 2) позволяют оценить степень и направление структурных взаимодействий процессов фазообразования, изоморфизма и растворимости в многочисленных системах, в том числе в молекулярных [5-6].
) от коэффициента α, единая для широкого класса структур (рис. 1). В ней значения α от 0 до 5 соответствуют условиям энтропийного равновесия, при котором ρ=100%. Этот вид номограммы и ее зеркально-симметричный вариант (рис. 2) позволяют оценить степень и направление структурных взаимодействий процессов фазообразования, изоморфизма и растворимости в многочисленных системах, в том числе в молекулярных [5-6].
Чем меньше величина α, тем выше степень волновой составляющей взаимодействия в соответствии с рисунком 2 (негэнтропийная кривая). А в рисунке 1 увеличение значений α характеризует нарастание корпускулярных и электростатических свойств в микросистемах (энтропийная кривая). Таким образом, понятие энтропии количественно моделируется через коэффициент α, а негэтропия через величину 1/ α.
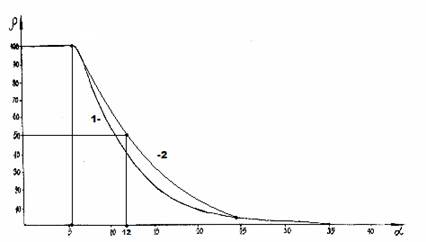
Рис. 1. Номограмма зависимости степени структурных взаимодействий (ρ) от коэффициента α
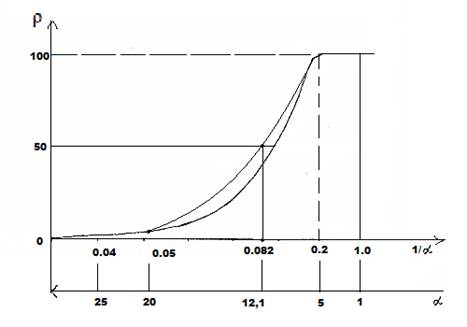
Рис. 2. Номограмма зависимости степени структурных взаимодействий (ρ) от коэффициента 1/α
Многие явления и процессы в природе, технике и даже в экономике описываются аналогичными графиками, которые называются S-кривыми. Такие S-кривые и исходные номограммы являются графическими характеристиками неравновесной динамики изменения энтропийных составляющих.
3. Условия равенства и соотношений энтропийных параметров
Выполнение пункта 3 исходных положений классифицируется в зависимости от особенности динамики процесса. Так в электромагнитной волне разность хода составляющих векторов равна 90°. В общем случае при вращательном движении системы из двух одинаковых по величине векторов (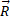 ) с разностью фаз 90° их равнодействующая:
) с разностью фаз 90° их равнодействующая:
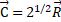 , где для данного угла tg45°=1 (6)
, где для данного угла tg45°=1 (6)
Если такой процесс дополняется движением по спиральной динамике, то вектор (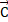 ) станет касательным вектором и образует угол спирального вращения, для которого:
) станет касательным вектором и образует угол спирального вращения, для которого:
tgφ = С/R = 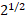 , где φ геодезический угол, равен 54,733° (7)
, где φ геодезический угол, равен 54,733° (7)
Под этим углом тутовый шелкопряд наматывает шелковую нить на основу.
Таким образом при чисто вращательном движении выполняется условие равенства составляющих векторов энтропийных характеристик, а при спиральном движении их соотношение равно 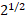 . При поступательном движении действуют условия или равенства или постоянного соотношения величин их составляющих. При этом в статистических процессах проявляются экспоненциальные зависимости. Такой подход определяет общие принципы многих физических закономерностей.
. При поступательном движении действуют условия или равенства или постоянного соотношения величин их составляющих. При этом в статистических процессах проявляются экспоненциальные зависимости. Такой подход определяет общие принципы многих физических закономерностей.
1) Характеристика спин-орбитального взаимодействия – постоянная тонкой структуры 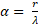 , где r – классический радиус электрона, λ – его комптоновская длина волны.
, где r – классический радиус электрона, λ – его комптоновская длина волны.
2) В работах [7; 8] используются понятия разрушающего напряжения при растяжении пластика нити на шаг ее намотки, где: σα – осевое, σβ – окружное напряжения заменяются пропорциональной им величиной Nα – осевое «усилие» и Nβ – окружное «усилие» по уравнению:
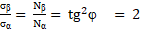 (8)
(8)
«Это условие позволяет получать равнонапряженную систему нитей с минимальной массой изделия» [8].
В гармонических колебаниях тела отношение потенциальной энергии обусловленной квазиупругой силой к кинетической энергии равно tg2δ, то есть:
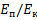 = tg2δ (8а),
= tg2δ (8а),
где δ – угловая характеристика колебаний.
При условии равенства δ=φ система получает энтропийное равновесное состояние.
3) В квантовой механике отношение магнитного момента частицы к ее механическому моменту называется магнитомеханическим (гиромагнитным) отношением – g. При этом gs = 2, если магнитный момент электрона обусловлен только спиновой составляющей и g = 1, если он создаётся орбитальным движением электронов. Такие значения g их соотношения характеризуют соответствующие энтропийные зависимости.
4) Уравнение Планка (квантовый переход):
h= E/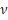 , где Е орбитальная энергия, в стационарном состоянии – величина постоянная, процесс идет по градиенту поля (энтропия),
, где Е орбитальная энергия, в стационарном состоянии – величина постоянная, процесс идет по градиенту поля (энтропия), 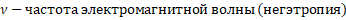 , h- постоянная Планка.
, h- постоянная Планка.
5) Уравнение скорости движения
V= S/t, где S – путь при механическом движении с затратой энергии (негэнтропия), t – время, всегда возрастает и направлено по градиенту (энтропия). Кривая Лоренца (рисунок не приводится) так же свидетельствует о проявлении пространственно-временной зависимости. Условием стационарного состояния в этих случаях является постоянство скорости движения, что выполняется как в микромире атомов и молекул, так и в макромире при движении планет.
6) При вращательном движении заряженой частицы в гравитационном поле [9]:
 )=
)=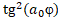 (9)
(9)
Где, 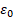 - электрическая постоянная,
- электрическая постоянная,
G — гравитационная постоянная,
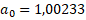 – квантовая поправка к гиромагнитному отношению электрона в атоме, которая возможно в данном случае характеризует влияние прецессии движения частиц.
– квантовая поправка к гиромагнитному отношению электрона в атоме, которая возможно в данном случае характеризует влияние прецессии движения частиц.
7) Из термодинамического определения энтропии следует:
T=dw/ds, где dw – тепловая энергия, поэтому средняя температура (T) является постоянно величиной, как в биологических системах, так и для планет.
8) В химической кинетике выполняется принцип Ле-Шателье: При внешнем воздействии на систему, находящуюся в равновесии, равновесие будет сдвигаться в направлении того процесса, который противодействует данному воздействию.
9) Исходные условия находятся в соответствии с Принципом дополнительности Н. Бора: для полного описания квантово-механических явлений необходимо применять два взаимоисключающих (дополнительных) набора классических понятий, совокупность которых дает исчерпывающую информацию об этих явлениях как о целостных. Например, описание объекта как частицы и как волны.
В таких примерах:
1. если процессы идут по градиенту (энтропия), то это параметры – t, 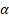 , E,
, E, 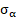 , r,
, r, 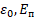 ;
;
2. Если процессы идут против градиента (негэтропия), то это параметры – S, 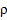 , ν,
, ν, 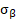 ,
,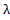 , µ, G,
, µ, G, 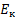 ,l.
,l.
5. S – кривые в экономике
S – кривые часто используются в экономических исследованиях, например: динамика ВВП, количество и объем продукции, прогнозирование инновационного потенциала и т.д. Так для оценки рациональной рыночной цены используются графики линии спроса (аналогия энтропии) и линии предложения (аналогия негэнтропии) – рис. 3 [10]
Из графика следует, что рациональная рыночная цена устанавливается при условии равенства линий спроса и предложения.
Показательна диаграмма мировой динамики ВВП, которая практически соответствует графику негэнтропии [11] – рис. 4. Основное уменьшение роста ВВП начинается с 2018 года и во время пандемии коронавируса становиться очень значительным.
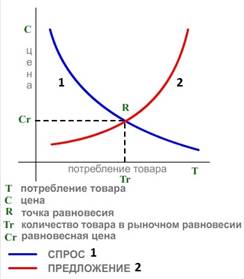
Рис. 3. График спроса и предложения
При этом ВВП Китая постоянно увеличивается, хотя и с замедлением даже в 2020 году. Чтобы не было стагнации ВВП возможно некоторым негэнтропийным экономикам необходимо дать небольшое дополнение энтропийной составляющей. В Мире уже есть опыт Китая и опыт борьбы с короновирусом. Так те государства, у которых процент госпредприятий был даже небольшим, быстрее сориентировались и лучше справляются с этой проблемой.
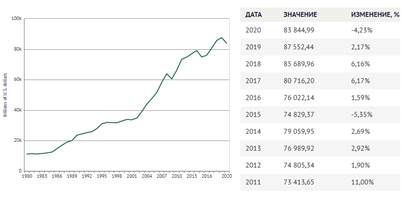
Рис. 4. График мирового ВВП.
6. S – кривые и COVID-19
Неравновесная динамика может проявляться в вирусной этиологии, которая может интерпретироваться как плавный переход от атомно-молекулярных взаимодействий на микроуровне к формально аналогичному процессу в макросистемах. Эта аналогия подтверждается графиком (рис. 5) для Российского сценария коронавируса [12] – в его наиболее сложный период, до появления омикронного вируса. Используя сравнительную методику с эталонными номограммами, можно сделать некоторые предположения о дальнейшем течении ковидного сценария [13].
Рис. 5. Количество заболеваний на данный момент времени.
7. Энтропийные принципы биоэнергетики
Биоэнергетика живых систем определяет широкий спектр их функциональных возможностей. И прежде всего – продолжительность жизни. Проблемы долголетия всегда изучались, и исследовались в мире, а их результаты учитывались и применялись, хотя с разным успехом в разное время. Наиболее резко длительность жизни людей стала расти после 20-х годов XX столетия, в основном, благодаря более развитой медицине (но не только). Для продления жизни человека теперь применяются генопротекторы, которые нормализуют нарушенные функции органов. Разработаны и используются методики лечения с применением статинов для снижения уровня холестирина низкой плотности.[14] Исследуются возможности генной инженерии, которая, меняя геном человека, могла бы способствовать в лечении наследственных болезней. В данной статье такие проблемные вопросы рассматриваются с позиции принципов энтропийных соотношений.
Так работает сердце: рабочая фаза (систола) всегда сопровождается функционально равноценной фазой отдыха (диастола). Давно установлено, что в тепловых процессах в открытой термодинамической системе энтропия полностью компенсируется потоком негэнтропии. Поэтому, условием статистической стабильности любой системы является равенство или паритетное соотношение этих энтропийных параметров. В неравновесной динамике такие энтропийные соотношения наглядно представляются в виде графиков, которые называют S-кривые. Например, кривые функциональных зависимостей параметров в эпидемиологических сценариях.
Для живых систем в плане их долголетия, и с позиции энтропийных соотношений, должны выполняться два простых общеизвестных правила:
1. Сколько калорий поглощается, ровно столько же их нужно расходовать.
2. Сколько живой организм отдыхает, столько же он должен работать (по времени и по интенсивности).
Вид питания имеет большое значение, но не всегда принципиальное по составу.
И нам важно и нужно понять, и правильно использовать такие принципы в своей биофизической философии, при построении энергообмена в собственной жизни, каким бы трудным этот подход не казался.
Заключение
Данный подход не является принципиально новым, и приведенные примеры - не единичны. В 1943 году Э. Шредингер в книге «Что такое жизнь?» объяснил, что в живой системе отрицательная энтропия, создаваемая организмом, уравновешивает поток положительной энтропии. Так, еще тысячи лет назад китайская медицина установила, что все явления мира и природы можно рассматривать как взаимодействие двух противоположных начал единой действительности. А в диалектике выполняется принцип единства и борьбы противоположностей.
С позиции этих представлений физиотерапию и рефлексотерапию можно рассматривать как методику выравнивания потенциалов двух проявлений энергетических начал, которыми по современным понятиям являются энтропия и негэнтропия. И природа в современной ситуации, как и раньше, выполняет свои принципы. Например: коллективным иммунитетом она борется против вируса. Двадцатый век – век войн эпидемий и революций имел большие человеческие потери. Но коэффициент прироста населения оказался самым высоким за всю историю человечества. В настоящее время экологических проблем есть актуальный принцип: сколько углекислого газа создается, столько его и должно поглощаться.
Установленные энтропийные принципы многопланово проявляются и в природе, и в технике, и могут эффективно использоваться.
Так, сотни лет тутовый шелкопряд наматывает шелковую нить на основу под углом 54,733 градуса (геодезический угол). В технике уже давно, при изготовлении космических аппаратов, специальная высокопрочная нить наматывается на корпус под тем же углом. Есть и другие менее известные примеры: при наматывании льна на основу или при работе некоторых устройств в сельскохозяйственной технике и т.д.
Поскольку эти закономерности неизвестны широкой научной общественности, то их применение в практике явно недостаточное. А учитывать эти принципы необходимо в технологии приготовления гибридной продукции, состоящей из двух или более компонентов (или фракций). Например, при изготовлении молокосодержащих составов. Полученная таким способом продукция будет качественно лучше обычной.
Особое значение имеет такая методология в материаловедении. Например, при легировании стали. В таких случаях возникают проблемные вопросы фазообразования и протяженности твердых растворов. Данный подход позволяет найти оптимальные решения для оценки степени взаимодействия атомно-молекулярных структур (ρ).
Используя данную энтропийную методику, и её номограмму, можно оценивать процессы изоморфизма, и формирования твердых растворов в простых и сложных системах.
Это и есть практические возможности применения данной методологии в научных исследованиях и в технологических новациях.
