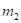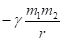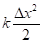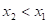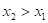Введение
При научных исследованиях в различных областях химической физики можно отметить высокую самоорганизацию и связь между многими природными явлениями и процессами. Например, в химической кинетике - принцип Ле-Шателье, а в физике – принцип дополнительности Н. Бора, и также проявляется при анализе эффективности параметров катализа. Несомненно, при этом действуют определенные общие принципы и закономерности.
Анализу глобальных процессов в живой и не живой системах посвящено много исследований.
В качестве примера можно привести статью Г.Р. Иваницкого [1]. В данной статье автор считает, что положения Э. Шредингера по соотношениям энтропийных составляющих в живой системе устарели. И для анализа глобальных процессов в живой и неживой материи он развивает метод химической кинетики.
Этот подход, конечно, может давать эффективные результаты, потому что нелинейная динамика химической кинетики находится в соответствии с принципами направленности процессов.
Например, это следует из принципа Ле-Шателье по химической кинетике:
? «При внешнем воздействии на систему, находящуюся в равновесии, равновесие будет сдвигаться в направлении того процесса, который противодействует данному воздействию». ? ? ? ? ? ?
Таким образом, значительный интерес имеет и проблема многопланового проявления понятия энтропии. Известно, что понятие энтропии, вытекающее из второго закона термодинамики, является критерием направленности процесса и степенью неупорядоченности систем. Поэтому, в данном исследовании делается попытка объяснения вышеуказанных проблем с позиции представлений о градиенте направленности физико-химических процессов при изменении их энтропийных составляющих.
- Исходные принципы.
Был проведен [2] анализ характера изменения величины потенциальной энергии 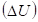 по ее знаку для различных потенциальных полей (таблица 1).
по ее знаку для различных потенциальных полей (таблица 1).
Получено, что значения –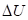 и соответственно
и соответственно 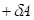 (положительная работа) соответствуют взаимодействиям, происходящим по градиенту потенциала, а +
(положительная работа) соответствуют взаимодействиям, происходящим по градиенту потенциала, а +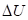 и
и  (отрицательная работа) имеют место при взаимодействиях против градиента потенциала.
(отрицательная работа) имеют место при взаимодействиях против градиента потенциала.
Таблица 1 – Направленность процессов взаимодействий
|
No |
Systems |
Type of potential field |
Process |
|
|
|
Sign
|
Sign
|
Process directedness in potential field |
|
1 |
opposite electrical charges |
electrostatic |
attraction |
|
|
|
- |
+ |
along the gradient |
|
repulsion |
|
|
|
+ |
- |
against the gradient |
|||
|
2 |
similar electrical charges |
electrostatic |
attraction |
|
|
|
+ |
- |
against the gradient |
|
repulsion |
|
|
|
- |
+ |
along the gradient |
|||
|
3 |
elementary masses |
gravitational |
attraction |
|
|
|
- |
+ |
along the gradient |
|
repulsion |
|
|
|
+ |
- |
against the gradient |
|||
|
4 |
spring deformation |
field of elastic forces |
compression |
|
|
|
+ |
- |
against the gradient |
|
extension |
|
|
|
+ |
- |
against the gradient |
|||
|
5 |
photoeffect |
electrostatic |
repulsion |
|
|
|
- |
+ |
along the gradient |
Поэтому, на основе анализа первого начала термодинамики было установлено:
1. В системах, в которых взаимодействие идет по градиенту потенциала (положительная работа) результирующая потенциальная энергия, как и приведенная масса, находятся по принципу сложения обратных значений соответствующих величин подсистем. Это – корпускулярный процесс, теоретической концепцией которого может являться энтропия.
2. В системах, в которых взаимодействие идет против градиента потенциала (отрицательная работа) выполняется алгебраическое сложение их масс и также соответствующих энергий подсистем. Это – волновой процесс, теоретической концепцией которого может являться негэнтропия.
3. Резонансное стационарное состояние систем выполняется при условии равенства степеней их корпускулярных и волновых взаимодействий. В термодинамике открытых систем продукция энтропии в стационарном состоянии полностью компенсируется потоком негэнтропии.
4. Все явления и процессы в природе и в Мире, включая человека, технику, экономику и экологию, идут только в двух энергетических направлениях. Или - по градиенту силового поля, с минимальной затратой энергии, или - против градиента, с максимальной затратой энергии. Первое направление соответствует понятию энтропия, а второе - понятию негэнтропия (отрицательная энтропия). В динамике процессов оба явления взаимосвязаны, и дополняют друг друга.
2. Графики S-кривых и энтропийные номограммы.
Еще Гейзенберг и Дирак[3] для оценки степени структурных взаимодействий предложили обменный гамильтониан, выведенный в предположении о прямом перекрывании волновых функций взаимодействующих центров:
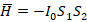 ,
,
где: 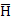 – спиновый оператор изотропного обменного взаимодействия для пары атомов,
– спиновый оператор изотропного обменного взаимодействия для пары атомов, 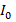 – постоянная обмена,
– постоянная обмена, 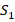 и
и 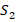 – интегралы перекрывания волновых функций.
– интегралы перекрывания волновых функций.
Каждая свободная атомная структура изначально имеет энтропийное равновесное состояние двух противоположных начал (орбиталь-ядро) в системе единой действительности (атом). В бинарной системе соответственно идут взаимодействия противоположных энтропийных составляющих от обоих атомов, пока не стабилизируется динамика энтропийного равновесия. Такие равновесно-обменные конформационные взаимодействия регулируют стабилизацию многих органических систем (кластеры, полипептидные цепи и т.д.). Поэтому, в данном подходе интегралы перекрывания волновых функций моделируются через величину относительной разности энергетических параметров взаимодействующих центров – коэффициент 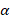 (в %). Такой параметр является прямой характеристикой степени энтропийного равновесия в системе. Исходные значения энергетических и размерных параметров для большинства элементов при разных валентно-активных орбиталях приведены в [2, 4, 5] и в других моих публикациях.
(в %). Такой параметр является прямой характеристикой степени энтропийного равновесия в системе. Исходные значения энергетических и размерных параметров для большинства элементов при разных валентно-активных орбиталях приведены в [2, 4, 5] и в других моих публикациях.
Применяя надёжные экспериментальные данные, получена номограмма зависимости степени структурных взаимодействий (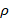 ) от коэффициента α, единая для широкого класса структур (рис. 1). В ней значения α от 0 до 5 соответствуют условиям энтропийного равновесия, при котором
) от коэффициента α, единая для широкого класса структур (рис. 1). В ней значения α от 0 до 5 соответствуют условиям энтропийного равновесия, при котором  =100%. Этот вид номограммы и ее зеркально-симметричный вариант (рис. 2) позволяют оценить степень и направление структурных взаимодействий процессов фазообразования, изоморфизма и растворимости в многочисленных системах, в том числе в молекулярных.
=100%. Этот вид номограммы и ее зеркально-симметричный вариант (рис. 2) позволяют оценить степень и направление структурных взаимодействий процессов фазообразования, изоморфизма и растворимости в многочисленных системах, в том числе в молекулярных.
Чем меньше величина α, тем выше степень волновой составляющей взаимодействия в соответствии с рисунком 2 (негэнтропийная кривая). А в рисунке 1 увеличение значений α характеризует нарастание корпускулярных и электростатических свойств в микросистемах (энтропийная кривая). Таким образом, понятие энтропии количественно моделируется через коэффициент α, а негэтропия через величину 1/ α.
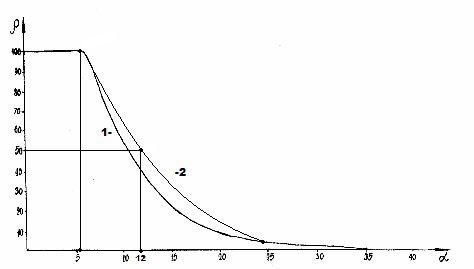
Рис. 1. Номограмма зависимости степени структурных взаимодействий (ρ) от коэффициента α
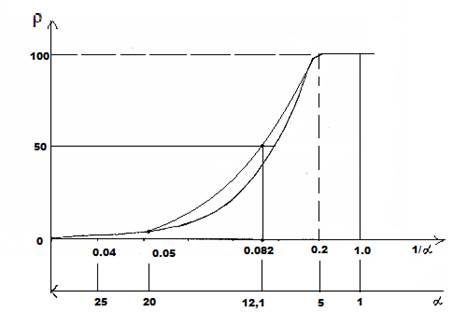
Рис. 2. Номограмма зависимости степени структурных взаимодействий (ρ) от коэффициента 1/α
Многие явления и процессы в природе, технике и даже в экономике описываются аналогичными графиками, которые называются S-кривыми. Такие S-кривые и исходные номограммы являются графическими характеристиками неравновесной динамики изменения энтропийных составляющих.
3. Условия равенства и соотношения энтропийных составляющих.
Выполнение пункта 3 исходных положений классифицируется в зависимости от особенности динамики процесса. Так в электромагнитной волне разность хода составляющих векторов равна 90°. В общем случае при вращательном движении системы из двух одинаковых по величине векторов (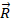 ) с разностью фаз 90° их равнодействующая:
) с разностью фаз 90° их равнодействующая:
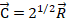 , где для данного угла tg45°=1 (1)
, где для данного угла tg45°=1 (1)
Если такой процесс дополняется движением по спиральной динамике, то вектор (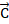 ) станет касательным вектором и образует угол спирального вращения, для которого:
) станет касательным вектором и образует угол спирального вращения, для которого:
tgφ = С/R = 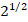 , где φ геодезический угол, равен 54,733° (2)
, где φ геодезический угол, равен 54,733° (2)
Под этим углом тутовый шелкопряд наматывает шелковую нить на основу.
Таким образом при чисто вращательном движении выполняется условие равенства составляющих векторов энтропийных характеристик, а при спиральном движении их соотношение является постоянной величиной, но при значении угла «намотки», равному геодезическому углу. При поступательном движении действуют условия или равенства или постоянного соотношения величин их составляющих. При этом в статистических процессах проявляются экспоненциальные зависимости. Такой подход определяет общие принципы многих физических закономерностей.
4. Некоторые примеры.
1) Характеристика спин-орбитального взаимодействия – постоянная тонкой структуры 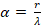 , где r – классический радиус электрона, λ – его комптоновская длина волны.
, где r – классический радиус электрона, λ – его комптоновская длина волны.
2) В гармонических колебаниях тела отношение потенциальной энергии обусловленной квазиупругой силой к кинетической энергии равно tg2δ, то есть:
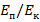 = tg2δ (3),
= tg2δ (3),
где δ – угловая характеристика колебаний.
При условии равенства 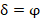 система получает энтропийное равновесное состояние.
система получает энтропийное равновесное состояние.
3) Уравнение Планка (квантовый переход):
h= E/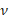 , где Е орбитальная энергия, в стационарном состоянии – величина постоянная, процесс идет по градиенту поля (энтропия), v - частота электромагнитной волны (негэнтропия), h- постоянная Планка.
, где Е орбитальная энергия, в стационарном состоянии – величина постоянная, процесс идет по градиенту поля (энтропия), v - частота электромагнитной волны (негэнтропия), h- постоянная Планка.
4) Уравнение скорости движения
V= S/t, где S – путь при механическом движении с затратой энергии (негэнтропия), t – время, всегда возрастает и направлено по градиенту (энтропия). Кривая Лоренца пространственно-временной зависимости (рисунок не приводится) так же свидетельствует об этих соотношениях. Условием стационарного состояния в этих случаях является постоянство скорости движения, что выполняется как в микромире атомов и молекул, так и в макромире при движении планет.
5) Из термодинамического определения энтропии следует:
T=dw/ds, где dw – тепловая энергия. Поэтому средняя температура (T) является постоянно величиной, как в биологических системах, так и в макромире.
6) В этом примере используются данные из [6]. При изготовлении космических аппаратов намотка высокопрочной нити на корпус проводится под геодезическим углом, в соответствии с энтропийными соотношеними:
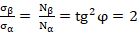 (4)
(4)
где: σα – осевое, σβ – окружное напряжения заменяются пропорциональной им величиной Nα – осевое «усилие» и Nβ – окружное «усилие».
Это условие позволяет получать равнонапряженную систему нитей с минимальной массой изделия.
7) В квантовой механике отношение магнитного момента частицы к ее механическому моменту называется магнитомеханическим (гиромагнитным) отношением – g. При этом gs = 2, если магнитный момент электрона обусловлен только спиновой составляющей, и g = 1, если он создаётся орбитальным движением электронов. Такие значения g, и их соотношения - характеризуют соответствующие энтропийные зависимости.
8) Принцип дополнительности Н. Бора: "Для полного описания квантово-механических явлений необходимо применять два взаимоисключающих (дополнительных) набора классических понятий, совокупность которых дает исчерпывающую информацию об этих явлениях как о целостных. Например, описание объекта как частицы и как волны".
5. О механизме гравитации.
Ньютоновская модель гравитации является чисто математической без какого-либо физического содержания.
Общая теория относительности Эйнштейна (ОТО) объясняет физическую сущность тяготения на основе понятия об изменении геометрических свойств и искривления 4-мерного пространства-времени.
Однако по современным представлениям «название ОТО является не адекватным и постепенно исчезает из литературы, заменяясь на теорию тяготения». Появились новые теории, уточняющие исходные принципы ОТО. Наиболее фундаментальной является квантовая теория гравитации, но она пока не считается законченной. Тяготение – единственное фундаментальное взаимодействие, по которому пока не построена общепризнанная непротиворечивая теория.
В данной работе делается попытка анализа таких проблем на основе представления о градиенте направленности корпускулярно-волновых процессов в системах различной природы.
При вращательном движении твердого тела (или математической точки) вокруг неподвижной оси вектор полного ускорения состоит из двух составляющих векторов: центростремительного ускорения и касательного ускорения.
Вектор центростремительного ускорения при неподвижной оси вращения направлен к ней, то есть по градиенту поля. Это корпускулярная часть движения. Вектор касательного ускорения направлен от системы по касательной к траектории, то есть против градиента поля – это волновая часть движения.
При аналогичном движении заряженных частиц происходит одновременно перенос ее массы и перенос заряда. Так в электродиффузионном уравнении переноса заряженных частиц общая интенсивность потока (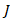 ) равна сумме интенсивностей переноса массы (
) равна сумме интенсивностей переноса массы (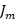 ) и переноса заряда (
) и переноса заряда (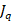 ):
):
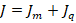 (5)
(5)
В соответствии с условием стационарного состояния (п.3 исходных данных) действие корпускулярной составляющей определяет появление волновой части процесса. Так круговое движение зарядов (корпускулярный процесс) дает магнитное поле с его полюсами (волновой процесс).При аналогичном движении массы заряженной частицы (корпускулярный процесс) должно возникать потенциальное поле (волновой процесс). Можно предположить, что такое поле является гравитационным, но тогда должно выполняться определенное соотношение между постоянной тяготения и электрической постоянной. Поэтому, применительно к кинематике механических систем, но сохраняя формализм исходных принципов, получаем:
 )=
)=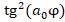 (6)
(6)
Где, 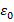 - электрическая постоянная, G - гравитационная постоянная
- электрическая постоянная, G - гравитационная постоянная
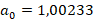 – квантовая поправка к гиромагнитному отношению электрона в атоме, которая возможно в данном случае характеризует влияние прецессии движения частиц. Данное уравнение выполняется с отклонением от исходного значения
– квантовая поправка к гиромагнитному отношению электрона в атоме, которая возможно в данном случае характеризует влияние прецессии движения частиц. Данное уравнение выполняется с отклонением от исходного значения 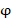 на 0,015%.
на 0,015%.
Таким образом, уравнение (6) подтверждает предположение о том, что волновой вклад массы заряженной частицы определяет наличие гравитационного поля, элементарными частицами которого могут быть гравитоны.
Поэтому сходство уравнений Кулона и Ньютона не является формальным, а имеет физическое обоснование. Кроме того, равенство гравитационной и инертной массы определяется равенством соответствующих корпускулярных и волновых составляющих.
Сила тяготения не зависит от химического состава тел или частиц. Каждое тело состоит из множества частиц в общем случае разных по природе и по размерам. При образовании гравитационного поля микросистемами, общим для всех структур представляется процесс протон-электронного взаимодействия под действием центральных сил. В неживой природе каждая система частиц, образующих данное тело может рассматриваться как закрытая. В таких случаях (согласно п.2 исходных данных) идет прямое алгебраическое сложение их интенсивностей независимо от химического состава частиц, образующих массу тела. При этом результирующая интенсивность гравитации прямо пропорциональна массе тела.
Но в живой природе каждая система является открытой, поэтому идут процессы взаимодействия ее с внешней средой, но с сохранением гравитацией специфических особенностей каждой частицы.
В любом живом организме выполняются сложные биоэлектрические процессы. Например, в молекуле ДНК при закручивании или раскручивании ее структурной спирали направление таких взаимодействий может идти по геодезическому углу.
В динамике конформации ДНК большое значение имеют так же протон-электронные взаимодействия между подсистемами этой молекулы. Возникающее при этом гравитационное поле несет в себе энергетическую и генетическую информацию от каждой молекулы ДНК.
В виду специфичности и слабой интенсивности такого поля, оно не регистрируется обычными приборами, но может контактировать с такими системами, которые способны настраиваться в резонанс с исходной системой. Очевидно, в этом и находится главная причина известных эффектов так называемой телепатии. Но это процесс биогравитации.
Выводы о механизме тяготения
1) Используя условие стационарного состояния в корпускулярно-волновых взаимодействиях и в рамках нерелятивистской механики проведен анализ механизма процессов тяготения.
2) Получено уравнение функциональной зависимости постоянной тяготения от электрической постоянной.
3) Предполагается, что тяготение есть волновой вклад от массы заряженных частиц при движении их в поле центральных сил.
6. S-кривые в экономике.
S – кривые часто используются в экономических исследованиях, например: динамика ВВП, количество и объем продукции, прогнозирование инновационного потенциала и т.д. Так для оценки рациональной рыночной цены используются [7] графики линии спроса (аналогия энтропии) и линии предложения (аналогия негэнтропии) – рис. 3
Из графика следует, что рациональная рыночная цена устанавливается при условии равенства линий спроса и предложения.

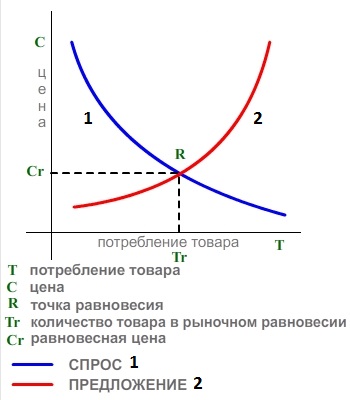
Рис. 3. График спроса и предложения
7. S-кривые в вирусной этиологии
Неравновесная энтропийная динамика проявляется в вирусной этиологии, которая может интерпретироваться как плавный переход от атомно-молекулярных взаимодействий на микроуровне к формально аналогичному процессу в макросистемах. Эта аналогия подтверждается графиком (рис. 4) для Российского сценария коронавируса в наиболее агрессивный период, до появления омикронного штамма[8].
Используя сравнительную методику с эталонными номограммами, можно делать некоторые предположения о дальнейшем течении ковидного сценария[9].

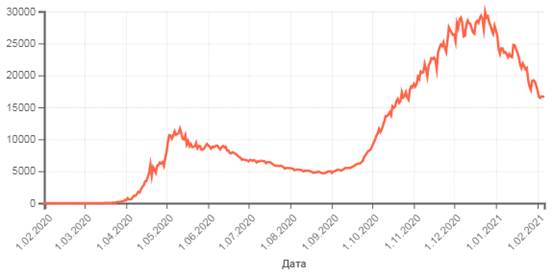
Рис. 4. Количество заболеваний на данный момент времени.
8. О биоэнергетике живых систем
Энтропийные принципы биоэнергетики живых систем определяет широкий спектр их функциональных возможностей. И прежде всего – продолжительность жизни.
Проблемы долголетия всегда изучались, и исследовались в мире, а их результаты учитывались и применялись, хотя с разным успехом в разное время.
Для продления жизни человека теперь применяются генопротекторы, которые нормализуют нарушенные функции органов [10].
Такие проблемные вопросы можно рассматривать с позиции принципов энтропийных соотношений.
Условием статистической стабильности любой системы является равенство или паритетное соотношение этих энтропийных параметров.
Так работает сердце: рабочая фаза (систола) всегда сопровождается функционально равноценной фазой отдыха (диастола). Поэтому для стабильной живой системы выполняется принцип: физическая активность и движение должны адекватно компенсироваться покоем и отдыхом. И наоборот. Аналогично в энергетике питания: сколько калорий поглощается, столько должно расходоваться.
Заключение
Данный подход применения энтропийной методологии не является принципиально новым, и приведенные примеры - не единичны. В 1943 году Э. Шредингер в книге «Что такое жизнь?» объяснил, что в живой системе отрицательная энтропия, создаваемая организмом, уравновешивает поток положительной энтропии. Так, еще тысячи лет назад китайская медицина установила, что все явления мира и природы можно рассматривать как взаимодействие двух противоположных начал единой действительности. А в диалектике выполняется принцип единства и борьбы противоположностей.
С позиции этих представлений физиотерапию и рефлексотерапию можно рассматривать как методику выравнивания потенциалов двух проявлений энергетических начал, которыми являются энтропия и негэнтропия. И природа в современной ситуации, как и раньше, выполняет свои принципы. Например: коллективным иммунитетом она борется против вируса.
В настоящее время экологических проблем есть актуальный принцип: сколько углекислого газа создается, столько его и должно поглощаться.
Поскольку исходные принципы этих закономерностей неизвестны широкой научной общественности, то их применение в практике явно недостаточное. А учитывать эти принципы необходимо, например, в технологии приготовления гибридной продукции, состоящей из двух или более компонентов (или фракций).? Полученная таким способом продукция будет качественно лучше обычной.
Особое значение имеет такая методология в материаловедении. В таких случаях возникают проблемные вопросы фазообразования и протяженности твердых растворов. Но данный подход позволяет найти оптимальные решения для оценки степени взаимодействия атомно-молекулярных структур.
Общие выводы:
1) Энтропийная методология функционально дает базисную основу физико-химических закономерностей во всех основных научных направлениях.
2) Адекватное применение геодезического угла в структурных взаимодействиях может повышать эффективность исходных энергетических параметров.
3) Приведённые в работе концепции дают теоретические и практические возможности использования энтропийной методологии в научных исследованиях и в технологических новациях.
Библиографическая ссылка
Кораблев Г.А. ЭНТРОПИЙНАЯ МЕТОДОЛОГИЯ ФИЗИКО-ХИМИЧЕСКИХ ПРОЦЕССОВ // Научное обозрение. Фундаментальные и прикладные исследования. 2023. № 3. ;URL: https://scientificreview.ru/ru/article/view?id=111 (дата обращения: 03.01.2026).
DOI: https://doi.org/10.17513/srfar.111

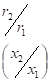
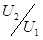
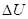
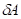
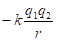
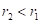
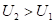
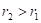
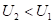
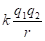
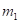 and
and