Введение
Матричные модели представляют собой модели, построенные в виде таблиц(матриц). Эти модели находят широкое применение при решении плановых и экономических задач и при обработке больших массивов информации. В курсе высшей алгебры часто встречаются материалы о вычислениях значений квадратных определителей. А словосочетание "неквадратный матриц", "определителей неквадратный матриц" есть, но до сих пор не были рассмотрены вопросы нахождения их значений. Поэтому в этой статье мы впервые вводим новое понятие "раскулантов ( определителей неквадратных матриц)" или значение раскулантов(значение определителей неквадратных матриц), и покажем методы их вычислений.
Цель исследования:
1.Раскрыть понятие раскулантов 1хn и mхn;
2.Выявить понятие значение раскулантов и показать методы их вычислений.
3.Найти общий способ решение диофантовых систем неопределенных уравнений;
Новизна исследования:
1.Впервые вводится новое понятие раскуланты и методы вычисления значений раскулантов 1хn, 2хп и mхn;
2.Определены взаимосвязи между теорией квадратных определителей и теорией раскулантов(неквадратных определителей).
3.Найдены методы вычисления значений следующих видов раскулантов 2х3 ,2х4,.. состоящих из двух строк, трех столбцов. Способы вычисления придуманы нами так:
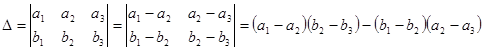
4.Правила применения при решении системы неопределенных уравнений методом вычисления значений раскулантов 2х3 ( состоящих из двух строк, трех столбцов),2х4( состоящих из двух строк, четырех столбцов)
Материал и методы исследования
При решении экономических задач применяются методы экономико-математического моделирования, использующие решение систем линейных алгебраических уравнений. Для изучения новых методов решения систем уравнений введем понятия раскулантов.
Определение. Таблица m x n чисел aij вида 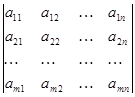 , состоящая из m строк и n столбцов, при m
, состоящая из m строк и n столбцов, при m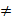 n, называется раскулантом.
n, называется раскулантом.
Числа aij, стоящие на пересечении i-й строки и j-го столбца, называются элементами раскуланта.
Раскуланты А=(аij) и В=(bij) называются равными, если они имеют одинаковые размеры и для каждой пары индексов выполняется равенство aij= bij.
В курсе алгебры решаются системы линейных уравнений с несколькими способами. Наши способы именуются под методом раскулантов. Этот метод является самым эффективным в решении системы неопределенных уравнений.
Систему m линейных уравнений с n неизвестными будем записывать в следующем виде:

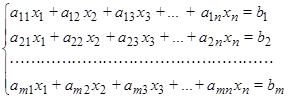 .
.
Здесь x1, x2, ¼, xn–неизвестные величины, aij (i = 1,2, ..., m; j =1, 2, ¼, n) – числа, называемые коэффициентами системы (первый индекс фиксирует номер уравнения, второй — номер неизвестной), b1, b2, ..., bm –числа, называемые свободными членами.
Решением системы будем называть упорядоченный набор чисел x1, x2, ..., xn, обращающий каждое уравнение системы в верное равенство.
Решить систему — значит найти все ее решения или доказать, что ни одного решения нет.
Система, имеющая решение, называется совместной.
Если система имеет только одно решение, то она называется определенной. Система, имеющая более чем одно решение, называется неопределенной (совместной и неопределенной).
Если система не имеет решений, то она называется несовместной.
Система, у которой все свободные члены равны нулю (b1 = b2 =...= bn = 0), называются однородными. Однородная система всегда совместна, так как набор из n нулей удовлетворяет любому уравнению такой системы.Если число уравнений системы совпадает с числом неизвестных (m=n), то система называется квадратной. Такие системы уравнений решаются при помощи метода Крамера.
Результаты исследования и их обсуждение.
В средней школе часто встречаются определенные и неопределенные уравнений.Для решение неопределенных уравнений работа Диофанта Александрийского является основами. Диофант Александрийский показал решения неопределенных уравнений и система уравнений различными искусственными методами, но общего метода решения до сих пор не найден . В курсе алгебры часто встречаются термины матрицы и определители. В работах известных ученых З.И.Боревич [2] , М.Оразбаев [3] , И.М.Виноградов [4], А.Г.Курош [5], Д.К.Фаддеев [6], В.Серпинский [7], В.А.Ильин [8] , А.И.Кострикин [9] , рассмотрены проблема матрицы и определителей. В работах указанных ученых больше всего рассматриваются квадратные матрицы и их определители. Однако, последние время некоторые ученые начали рассматривать не квадратные матрицы и вычислять значения их определителей. Например, Х.Минк [10]
. В курсе алгебры часто встречаются термины матрицы и определители. В работах известных ученых З.И.Боревич [2] , М.Оразбаев [3] , И.М.Виноградов [4], А.Г.Курош [5], Д.К.Фаддеев [6], В.Серпинский [7], В.А.Ильин [8] , А.И.Кострикин [9] , рассмотрены проблема матрицы и определителей. В работах указанных ученых больше всего рассматриваются квадратные матрицы и их определители. Однако, последние время некоторые ученые начали рассматривать не квадратные матрицы и вычислять значения их определителей. Например, Х.Минк [10]
(такие матрицы он называл неквадратные матрицы или перманентам) рассматривал неквадратные матрицы и вычисления их определителей, но его метод очень сложно и он как признал его метод для решения уравнении не пригоден. Поэтому мы определителей не квадратных матриц называли раскулантами, их виды очень много. Ввиду многочисленности их, мы старались, каждому виду дать отдельно определение и дать метод вычисления их значений. И так, одну из тысялетних проблем, мы при помощи раскуланта сумели решить( по нашему мнению). Наш метод решения неопреденных уравнений и систем, возможно, применим во многих областях математики. Мы ограничимся только некоторыми видами уравнений.
В этой работе метод нахождения корней неопределенных уравнений и систем заменяется методам нахождения значений раскулантов. Закономерно встают вопросы:
1. Существует ли связь между теорией квадратных определителей и теорией раскулантов (неквадратных определителей)?
2. И можно ли связать методы нахождения значений раскулантов (неквадратного определителя) с методом нахождения значений квадратных определителей?
Чтобы ответить на эти вопросы мы вводим понятия следующих трех определений.
1-определение. Имеет место равенство для 3-х столбцового, 2-х строчного раскуланта (неквадратного определителя) с 2-х столбцовым, 2-х строчным квадратными определителями.
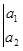
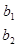
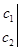 =
=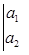

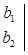 -
- 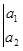
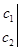 +
+ 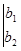
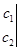 (1)
(1)
2-определение. Имеет место равенство 4-х столбцового , 2-х строчного раскуланта (неквадратного определителя) и 6-ти 2-х столбцовых , 2-х строчных квадратных определителей.
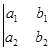
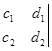 =
=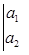

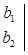 - 2
- 2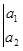
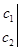 +
+ 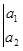
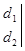 + 3
+ 3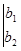
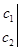 -2
-2 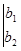
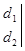 +
+ 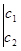
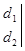 (2)
(2)
3-определение. Имеет место равенство 5-ти столбцового, 2-х строчного раскуланта (неквадратного определителя) и 10-ти 2-х столбцовых, 2-х строчных квадратных определителей.
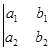
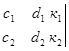 =
= 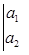

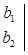 - 3
- 3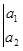
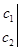 -
-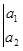
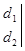 -
- 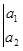
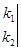 + 2
+ 2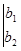
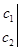 - 8
- 8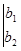
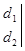 -
-
-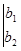
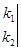 + 6
+ 6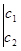
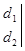 - 3
- 3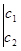
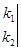 +
+ 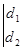
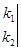 (3)
(3)
Теперь покажем, как мы пришли к этому выводу, т.е. результаты использования методов вычисления значений раскулантов и новый способ решения системы неопределенных уравнений.
При решении любых таких систем неопределенных уравнений, как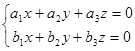
и 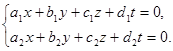 не применим метод Крамера.
не применим метод Крамера.
Мы поставили себе такой вопрос: Как в этом случае действовать? Мы словесно(совершенно случайно) ввели новое виды раскулантов 2х3 (неквадратных определителей) состоящих из двух строк, трех столбцов. Мы вычисляли значения нижеследующих раскулантов 2х3 (неквадратных определителей), различные способы вычисления придуманы нами так:
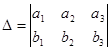 =
=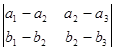 =
=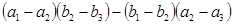 ;
;
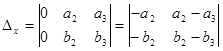 =
=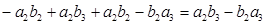 ;
;
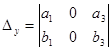 =
=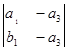 =
=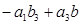 ;
;
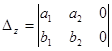 =
=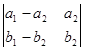 =
=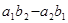 ;
;
Далее нашли неизвестные ( как у способа Крамера) нижеследующими формулами:
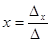 ;
; 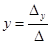 ;
; 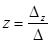 ;
;
Итак , общее решение находим с помощью нижеследующих равенств:
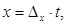
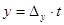 ,
, 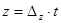 .
.
Здесь t: 0,± 1, ± 2,± 3 ...
Теперь приведем решение нескольких таких систем уравнений.
Пример 1 :
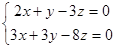 (1)
(1)
Решите системы уравнений. Такие уравнения называются однороднымы. Любые однородные системы неопределенных уравнений можно решить нашими способами.
Решение:
Решим вышеприведенную систему уравнений(1) с помощью метода нахождения раскулантов (находим воспользовавшись формулой (1) , значения неквадратных определителей с двумя строками, с тремя столбцами).
Вычисляем значения нижеследующих 2х3 раскулантов, состоящих из двух строк, трех столбцов :
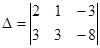 =11,
=11, 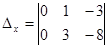 = 1,
= 1, 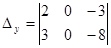 =7,
=7, 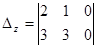 =3
=3
Тогда,можно найти частное решение 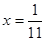 ,
,  ,
, 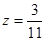 . Общее решение системы уравнений находим равенствами:
. Общее решение системы уравнений находим равенствами:  ,
, 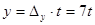 ,
, 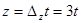 Здесь t: 0,± 1, ± 2,± 3 ...
Здесь t: 0,± 1, ± 2,± 3 ...
Пример 2.
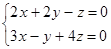 Вычисляем следующие значения неквадратных определителей с двумя строками, с тремя столбцами:
Вычисляем следующие значения неквадратных определителей с двумя строками, с тремя столбцами:
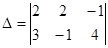 =-12,
=-12,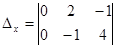 =7,
=7, 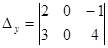 =-11,
=-11, 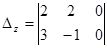 =-8;
=-8;
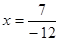 ,
, 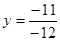 ,
, 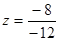 .
.
2. 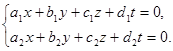 (2)
(2)
Для решения таких уравнении вычисляем нижеследующие раскуланты.
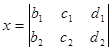 ,
,  ,
, 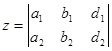
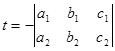 .
.
Привидем примеры решения следующих систем неопределенных уравнений.
Пример 3
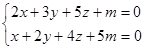
Решение:
х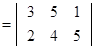 =10,
=10, 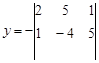 =-15,
=-15,
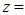
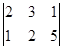 =5,
=5, 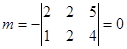 .
.
Общее решение имеет вид:
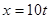 ,
, 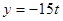 ,
, 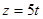 , т
, т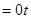 , где
, где 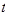 -любое число.
-любое число.
Пример 4 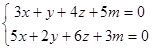
Решите системы уравнений. Решение:
х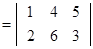 =-13 ,
=-13 , 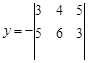 =4 ,
=4 , 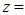
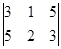 =10,
=10, 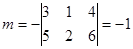 .
.
Общее решение: 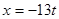 ,
, 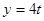 ,
, 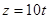 , т
, т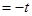 . где
. где 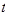 -любое число.
-любое число.
Пример 5 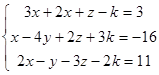
Решите системы уравнений.
Решение: Вычисляем нижеследующих раскулантов 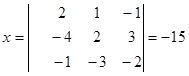
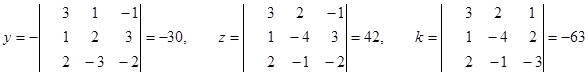

Общее решение: x=-15t, y=-30t, z=42t, k=-63t, где 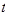 -любое число.
-любое число.
Выводы
Мы анализируя разные способы и методы решения однородных неопределенных систем уравнений пришли к такому мнению:
1.Для решения любого однородного 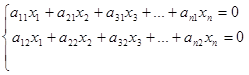 системы неопределенных уравнений можно использовать раскуланты состоящие из 2 строк и n стобцов. Из этого исходит то, что в любом случае можно решить систему уравнений состоящую из n – неизвестных, m – уравнений, с помощью раскулантов типа n строк и m столбцов.
системы неопределенных уравнений можно использовать раскуланты состоящие из 2 строк и n стобцов. Из этого исходит то, что в любом случае можно решить систему уравнений состоящую из n – неизвестных, m – уравнений, с помощью раскулантов типа n строк и m столбцов.
2.Для решения любого неоднородного 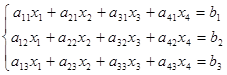 системы неопределенных уравнений также используем раскуланты состоящие из 3 строк и n стобцов.
системы неопределенных уравнений также используем раскуланты состоящие из 3 строк и n стобцов.
Библиографическая ссылка
Ибрагимов Р., Киргизбаев Ж., Парманов М. ПРИМЕНЕНИЕ РАСКУЛАНТОВ ПРИ РЕШЕНИИ НЕОПРЕДЕЛЕННЫХ УРАВНЕНИЙ И СИСТЕМЫ УРАВНЕНИЙ // Научное обозрение. Фундаментальные и прикладные исследования. 2018. № 1. ;URL: https://scientificreview.ru/ru/article/view?id=16 (дата обращения: 18.01.2026).
