1.Введение. Основные определения многокритериальной оптимизации.
Предположим, что задана математическая модель исследуемой системы,
и модель эта зависит от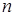 
параметров 
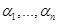. Пусть a =( 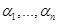). Как правило, специалисты задают пределы изменения каждого из параметров, которые мы будем называть параметрическими ограничениями
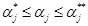
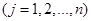. (1)
Ограничения (1) выделяют в пространстве параметров параллелепипед П.
Кроме параметрических ограничений обычно в условия задачи включаются функциональные ограничения
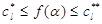
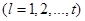. (2)
Здесь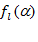 
— некоторые непрерывные функции от параметров.
Имеются критерии качества - непрерывные функции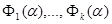 
которые желательно уменьшить. Очевидно, что не все значения 
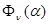одинаково приемлемы в смысле допустимого функционирования системы. Чтобы избежать такой ситуации необходимо ввести критериальные ограничения
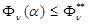
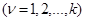. (3)
Критериальное ограничение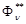 
— это максимальное (минимальное) допустимое значение критерия .
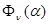Пусть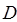 
— множество точек 
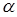, которые удовлетворяют всем ограничениям (1), (2) и (3).Естественно назвать 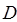множеством допустимых точек(параметров).
Сформулируем одну из основных задач векторной оптимизации.
Необходимо найти такое множество Р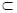
D, для которого
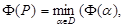(4)
где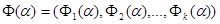 
- вектор критериев [1].
Р называется множеством Парето, также как его образ в пространстве критериев -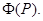 
Предположим, что критерии являются непрерывными функциями, удовлетворяющими условию Липшица, т.е. для всех векторов a и b из области определения критерия Фn существует число Ln такое, что
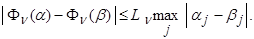
Или эквивалентно: существует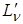 
такое что
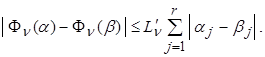
2. Цель исследования.
Целью данного исследования является создание методов и алгоритмов аппроксимации и регуляризации множества Парето – оптимальных решений.
Задача построения множества Парето достаточно сложна. Это объясняется тем, что аппроксимируя допустимое множество с заданной точностью, нельзя гарантировать аппроксимацию множества Парето. Такие задачи называются некорректными по Тихонову. В ряде работ предлагается решение этой проблемы при достаточно сильных ограничениях, накладываемых на критерии или систему предпочтений специалиста. Предлагаемые ниже результаты получены только в предположении о непрерывности критериев и выполнении условия Липшица [2].
3.Материалы и методы исследования.
Пусть P – множество Парето в пространстве параметров; Ф(P) – его образ; e - набор допустимых погрешностей. Необходимо построить конечное множество Парето Ф(Pe), аппроксимирующее Ф(P) с точностью до e .Пусть Ф(De) - e-аппроксимация Ф(D) и Pe - Парето-оптимальное подмножество в De. Как уже говорилось, задача аппроксимации Ф(P) является некорректной по Тихонову. Приведем определение этого понятия. Пусть P - функционал (оператор) на пространстве X, P: X®Y. Предположим, что существует y* = inf P(x), и Ve(y*) - окрестность искомого решения y*. Выделим элемент x* (или множество элементов) в пространстве X и его d-окрестность Vd (x*). Назовем решением задачи нахождения экстремального значения функционала P такое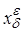 
, которое одновременно удовлетворяет условиям 
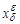ÎVd (x*) и P(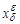)ÎVe (y*). Если по крайней мере одно из этих условий не вынолняется при произвольных e и d, то такая задача называется некорректной по Тихонову.
Аналогичное определение может быть дано в случае, когда P - оператор из пространства X в пространство Y. Пусть X={Ф(De), Ф(D)}; Y={Ф(Pe), Ф(P)}, где e® 0, и пусть P : X ® Y - оператор, сопоставляющий каждому элементу из X его Парето оптимальное подмножество. Тогда в соответствии с ранее сказанным, задача построения множеств Ф(De) и Ф(Pe), принадлежащих одновременно e-окрестностям Ф(D) и Ф(P) соответственно, является некорректной по Тихонову. В этом случае в пространствах X и Y должна быть определена метрика или топология [2,3], соответствующая системе предпочтений специалиста на Ф(D).
Зададим топологию на Х с помощью окрестности произвольной точки х. Пусть
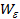(x) cостоит из таких Ф(De), что для любых Ф(a ) Îх, существует Ф(b)ÎФ(De), для которого 
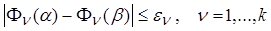. Либо к 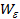(x) принадлежат такие Ф(De),что для любых Ф(a ) Î Ф(De) существует Ф(b)Îх такое, что 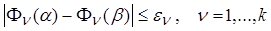. Аналогично зададим окрестность 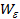(у) для произвольного у Î У, а значит и топологию на У.Зададим Ve-окрестность точки Ф(a0)ÎФ(П)
.
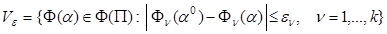В приведенной ниже теореме 3 строится Парето оптимальное множество, Ф(Pe) , в котором для любой точки Ф(a0)Î Ф(P) и любой ее e-окрестности Ve имеется точка Ф(b)ÎФ(Pe), принадлежащая Ve. Обратно, в e-окрестности любой точки Ф(b)ÎФ(Pe) существует точка Ф(a0)ÎФ(P). Множество Ф(Pe) называется аппроксимацией, обладающей свойством M Пусть построена Ф(De)-аппроксимация множества Ф(D).
Будем говорить, что аппроксимация Ф(Pe) обладает свойством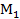 
, если для любой точки Ф(a0)ÎФ(P) любой ее e-окрестности Ve существует точка Ф(b)ÎФ(Pe), принадлежащая Ve .
Пусть имеется Ф(De) – аппроксимация Ф(D) [4,5].
Лемма 1.Если критерии непрерывны и удовлетворяют условию Липшица, то существует аппроксимация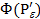 
, обладающая свойством .
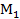Доказательство. Доказательство леммы проводится с помощью анализа окрестностей т.н. подозрительных точек из Ф(De), т.е. таких точек, в окрестностях которых могут находиться истинно паретовские точки. Если в окрестностях подозрительных точек имеются новые Парето-оптимальные решения, то они добавляются к Ф(Pe). Вместе с Ф(Pe), они образуют искомую e-аппроксимацию множества Парето. Определим множество подозрительных точек. Рассмотрим некоторую точку
Ф(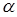)ÎФ(Pe), и пусть 
=
,
= 
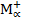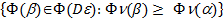
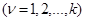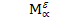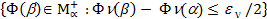при некотором n. Пусть
= 
(
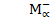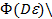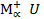Ф(Pe)), 
=
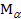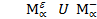, М =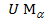
.
Рассмотрим Ф(a0) из М. Если для нее не найдется в Ф(Pe) ни одной точки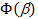 
такой, что 
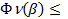Фn(a0) - en ,то Ф(a0) будем называть подозрительной точкой. Множество подозрительных точек обозначим ПМ.
Нетрудно видеть, что только в e-окрестностях точек из ПМ могут лежать точки из Ф(Р), не аппроксимированные с точностью до e множеством Ф(Pe).Таким образом, если мы построили куб 
с центром в некоторой точке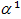 
такой, что Ф(
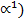Î ПМ,
и длиной ребра min 2en /Ln 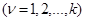, то этот куб может содержать Парето - оптимальные точки из Ф(Р),не аппроксимированные ни одной точкой из Ф(Pe).
Пусть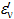 
-столь малые погрешности, которыми можно пренебречь. Аппроксимируем пересечение множеств Ф(
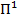) и Ф(D) с точностью до 
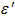.По крайней мере одна из рассматриваемых точек в принадлежит окреcтности Парето -оптимальной точки Ф(a0), если такая точка существует. Обозначим такую точку Ф(µ). Если Ф(a0) – паретовская точка, то Ф(µ) улучшает значение по крайней мере одного критерия произвольной точки
Ф(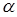)ÎФ(Pe).Если такая Ф(µ) существует, то добавляем ее к Ф(Pe). В противном случае не содержит точку Ф(a0) ÎФ(P) с точностью до 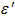.Эта операция повторяется для всех точек,
принадлежащих ПМ. Пусть UФ(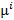
) U Ф(Pe) = Ф(
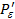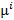) и U U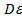
= 
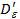для всех i , где 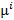- точка, полученная после выполнения упомянутой процедуры. Так что Ф(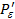) может содержать точки, которые не являются Парето-оптимальными и должны быть отброшены. В результате мы получаем множество Ф(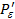), которое является парето- оптимальным подмножеством в Ф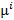(U U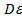 ) и e -аппроксимацией Ф(P). Это завершает доказательство леммы.
Полученная таким образом аппроксимация Ф(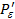) обладает свойством 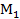.Однако, обратное утверждение, в общем случае, не верно, т.к. Ф(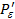) может содержать лишние точки, анализ которых бесполезен.
Будем говорить, что аппроксимация Парето- оптимального множества Ф(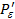), построенного в лемме 1, обладает свойством 
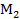, если существует точка 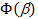ÎФ(P) внутри e -окрестности любой точки из 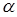Ф()ÎФ() .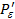
Лемма 2. Существует подмножество Ф(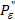
) множества Ф(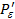),обладающее свойством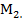 
Доказательство. Пусть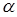 Ф()ÎФ(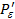) , В – произвольное подмножество в
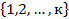и 
= 
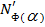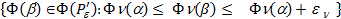для
любого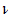 
из В.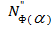
=
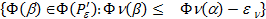для любого
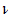
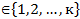В. Пусть также 
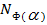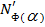=U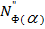 
. Как и ранее будем исследовать окрестности точек 
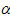и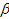 
, для которых 
.
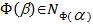Если для всех точек Pτ –сетки [1], принадлежащих кубам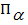 
и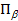 
и, удовлетворяющих предыдущим требованиям для аппроксимации допустимых множеств
выполняется условие: для любого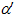 
, принадлежащего пересечению 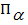и 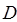существует µ, принадлежащая пересечению 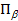и 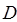так, что имеет место 
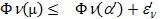для любого 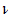из В, где 
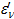-достаточно малая величина, то точку Ф(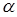) можно исключить из Ф(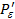), т.к. ее e-окрестность не содержит какой либо точки из Ф(P). Проводя аналогичную процедуру для всех 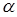Ф()ÎФ(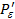), мы получим подмножество Ф(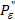) множества
Ф(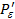),обладающее свойством 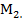Нетрудно показать, что с помощью процедур, описанных в леммах 1 и 2, и вычисляя Ф(),
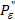мы в действительности доказали следующее:
Теорема 3. Если критерии непрерывны и удовлетворяют условию Липшица, то Ф(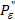)- есть аппроксимация множества Парето Ф(P),
обладающая свойством M.
Пусть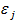 
- сходящаяся к 0, убывающая последовательпость положительных чисел. Известно, что решение некорректной задачи, какой является задача аппроксимации множества Парето, сводится к построению регуляризирующей последовательности. В данном случае это последовательность множеств Ф(
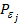), j=1,2,… ,такая, что для любой соответствующей последовательности Ф(
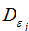) и любых 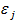– окрестностях множеств Ф(P) и Ф(D), множества Ф(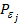) и Ф(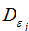), начиная Ф(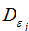) с некоторого 
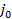, принадлежат соответствующим окрестностям.
Предположим, что в соответствии с леммами 1 и 2 последовательности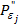 Ф(
), Ф(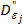
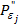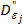), , построены для последовательности 
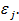Тогда справедлива следующая
Теорема 4. Последовательность Ф(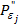) – регуляризирующая.
Доказательство. Из свойства М, справедливого для любого Ф(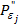), и определения окрестностей 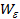(Ф(P)) и 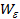(Ф(D)) непосредственно следует, что условия, определяющие регуляризирующую последовательность, выполнены.
4. Результаты исследования и их обсуждение.
В ряде работ решается задача регуляризации множества Парето при помощи метрики Хаусдорфа. Известно, тем не менее, что построить на допустимой области решений метрику, соответствующую системе предпочтений специалиста, невозможно или весьма затруднительно. Класс задач, описываемых метрикой Хаусдорфа, весьма узок, т.к. при применению ее к сколько - нибудь общему случаю, как правило произойдет искажение структуры предпочтений специалиста. Кроме того возникает вопрос: почему эта метрика должна порождаться каким- либо наперед заданным расстоянием? Ведь с изменением этого расстояния может измениться сходимость.
Поэтому в общем случае необходимо введение топологии, подобно тому, как это делалось выше. Эта топология является обобщением метрики Хаусдорфа, но при этом не искажает систему предпочтений специалиста.
Так как в практических задачах многокритериального проектирования количество векторов, принадлежащих множеству Парето-оптимальных решений, невелико вследствие наличия сильных функциональных и критериальных ограничений, то процедура исследования окрестностей подозрительных точек конструктивна, т.е. реализуема на компьютере в приемлемое время. Если, тем не менее для решения какой-либо конкретной задаче потребуется слишком много времени, то его можно сократить следующим образом. После аппроксимации Ф(D) множеством Ф(De) выделим из него Парето- оптимальное подмножество Ф(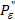) и множество подозрительных точек. Их объединение будет e - аппроксимацией множества Ф(P).
Аналогично можно получит аппроксимацию и регуляризацию множества Парето в пространстве параметров. Последнее особенно важно для решения задач многокритериальной идентификации.
5. Выводы
1. Разработана методика аппроксимации множества Парето-оптимальных решений с заданной точностью.
2. Приведен алгоритм аппроксимации.
3. Решена задача регуляризации множества Парето.
Библиографическая ссылка
Матусов Л.Б. О РЕГУЛЯРИЗАЦИИ МНОЖЕСТВА ПАРЕТО В ЗАДАЧАХ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ // Научное обозрение. Фундаментальные и прикладные исследования. – 2020. – № 1. ;URL: https://scientificreview.ru/ru/article/view?id=76 (дата обращения: 30.12.2024).