Введение. Проблема доказательства Великой теоремы Ферма в свете математической психологии.
Проблема интерпретации Великой теоремы Ферма (сокращенно ВТФ), возникающая при изучении ее основного уравнения:
zn = xn + yn (1)
где z, x, y, n – положительные целые числа, n > 2, постепенно осознавалась и прояснялась автором по мере продвижения его интуитивного подхода к доказательству теоремы в различных научных изданиях [1, 2, 3]. Данный подход следует отнести к области математической психологии, разрабатывающей математические средства описания психологических объектов. Психологическими объектами в данном случае являются все интеллектуально воспринимаемые математические объекты с известными и неизвестными отношениями между ними. Метод исследования в математической психологии заключается в нахождении новых математических свойств воспринимаемых объектов с помощью правдоподобных рассуждений, не всегда совпадающих со стандартами профессионального языка, и процедуре их использования для решения какой-либо математической задачи (прикладной или фундаментальной). Содержательная и эвристическая сторона математической психологии хорошо была раскрыта в известных книгах Д. Пойа «Математическое открытие» и «Математика и правдоподобные рассуждения».
Однако, излишняя полемичность статьи [3] и последующих за ней [4, 5, 6] не позволила автору четко изложить идею доказательства в строгих математических рамках, к чему автор вплотную подошел лишь в своих последних работах [7, 8, 9]. Эта идея коренится в проблеме интерпретации ВТФ, рассматриваемой с позиций различных математических объектов, представляющих утверждение ВТФ или приводящих к нему посредством каких-либо преобразований. Такими объектами могут быть либо абстрактные числа в виде целых, рациональных или других действительных чисел, либо это могут быть какие-либо числа, наполненные геометрическим содержанием. Выбор математических объектов для решения проблемы Ферма является принципиальным и определяет весь дальнейший ход рассуждений вплоть до получения конечного результата. Неопределенность в этом вопросе может привести к методологическим ошибкам и неверным результатам. Именно о таких задачах с неопределенным смыслом говорил Гаусс как об утверждениях, которые невозможно ни доказать, ни опровергнуть в какой-либо известной формальной системе Чаще всего эти предложения формулируются относительно самых простых очевидных объектов. Таким предложением и является теорема Ферма о целых числах.
В работе [2] отмечалось, что проблема интерпретации ВТФ лежит в основаниях математики, в частности, в аксиоматических представлениях о числовых множествах. Выяснилось [3], что теорема Ферма не укладывается в прокрустово ложе линейной действительной оси, когда существует взаимно однозначное соответствие между множеством действительных чисел и множеством точек, равномерно расположенных на всей прямой. Другими словами, существуют такие действительные числа (например, арифметические квадратные корни из целых чисел), для операций с которыми нужны другие аксиоматические формы и, значит, аналитическая теория чисел должна быть дополнена новой аксиоматикой геометрического представления чисел, а последняя может взяться только из опыта и окружающей действительности. Все эти моменты не были учтены в доказательстве Уайлса ВТФ [4], что привело, в конечном счете, к иллюзорной эллиптической кривой, не существующей в линейном топологическом пространстве, и замыканию доказательства в «порочном круге» [5].
В работе автора [6] и последующих проблема интерпретации ВТФ решается феноменологически, т.е. предлагается рассматривать отдельные члены уравнения Ферма (1) в виде совокупности единичных многомерных кубиков, из которых следует построить три больших многомерных куба, удовлетворяющих уравнению (1) (это построение иллюстрируется геометрически с учетом аксиоматических свойств чисел, входящих в уравнение Ферма). Такой геометрический подход для изучения и решения проблемы Ферма высвобождает огромный потенциал скрытых возможностей аксиоматического построения числовых соотношений. Он также лежит в основе всех квантовых теорий современной науки. В нашем случае единичные многомерные объекты теоремы Ферма и их совокупности можно считать квантами натуральных чисел [7]. Запись теоремы Ферма в виде обозначений из абстрактных целых чисел без учета их геометрического содержания не оставляет никаких шансов для более глубокого проникновения в мир чисел. Так, например, если разделить уравнение Ферма с взаимно простыми z, x, y на zn -1, то получим разбиение z на дроби, а не целые части, как можно было бы ожидать при квантовом подходе и увеличении масштаба уравнения (1). Однако, подбирая общий масштабный множитель для всех членов уравнения Ферма, можно получить подобное разбиение (1) в целых числах и, значит, уравнение Ферма обладает свойством масштабной инвариантности, называемым в квантовой теории скейлингом. При этом степенная структура уравнения Ферма (1), записанного в виде разбиения: (z’d)n = (x’d)n + (y’d)n, где целое число d не является взаимно простым с z’, x’, y’ , сохраняется в скрытом виде. С классической точки зрения, такое умножение сущности (примитивных троек Ферма с взаимно простыми z’, x’, y’) является сущим безумием, нарушающим закон достаточного основания, известный как принцип экономии мышления или «бритва Оккама».
Чтобы получить подобное разбиение (1) в целых числах для степеней z и z2, надо осуществить правильную калибровку уравнения Пифагора, получаемого масштабированием вниз из уравнения Ферма. В результате проведенной калибровки получаем уравнение Пифагора для чисел, названных прямоугольно-треугольными (или просто прямоугольными), являющимися арифметическими квадратными корнями из целых чисел: а + в = с, где а, в, с – целые числа. Среди множества прямоугольных чисел могут оказаться пифагоровы тройки чисел, так что а, в, с будут квадратами целых чисел. Пифагоровы тройки являются определяющими при построении степеней целых чисел в уравнении (1). Ниже будет показано, что сама структура уравнения Ферма однозначно определяет подобное разбиение (1) в виде уравнения Пифагора в целых числах. Однако спонтанное происхождение пифагоровых троек на всем множестве целых чисел остается загадкой, лежащей в основаниях квантовой теории чисел. Здесь важно также отметить, что именно прямоугольные числа являются операторами рождения и уничтожения квантов физических полей, определяющими амплитуды квантовых процессов. С точки зрения происхождения целых чисел, прямоугольные числа являются генераторами натурального ряда чисел.
Перейдем теперь к рассмотрению проблемы ВТФ с точки зрения ее возможного доказательства в интерпретации гипотезы Биля [8, 9], которая утверждает, что если уравнение (1) существует, где x, y, z – положитедьные целые числа, а показатель степени n может одновременно иметь спектр значений: n = (m ,p, q,) ≥3 при независимом значении n для каждого терма, то x, y, z имеют общий множитель. Фактически гипотеза Биля, как Обобщенная теорема Ферма, констатирует масштабную инвариантность уравнения (1), выражающуюся в подобных разбиениях различных степеней z на две целые части. Другими словами, предполагается, что если обобщенное уравнение (1) существует в виде суммы натуральных чисел: А + В = С, где C = zm , A = xp , В = yq, то А, В, С имеют общий делитель zm-1. Это означает, что натуральное число z также может быть разбито на сумму натуральных чисел вследствие масштабной инвариантности уравнения (1) (если это не так, то уравнение (1) не может быть записано в натуральных числах).
Рассмотрим уравнение (1) как разбиение целой степени zn на сумму других целых степеней xn и yn . Основания целых степеней также могут быть разбиты на целые части, исходя из квантовой парадигмы, при этом уравнение (1) можно представить как уравнение Пифагора:. z2 = xn/ zn–2 + yn/ zn–2 , в котором целые числа слагаемых трактуются как квадраты арифметических корней из тех же чисел. Введем теперь понятие прямоугольного числа (эти числа, вообще говоря, отличны от чисел прямоугольного треугольника, называемых пифагоровыми тройками, хотя и включают их в свое множество). Прямоугольное число – это такое неотрицательное действительное число, квадрат которого есть целое неотрицательное число. Множество прямоугольных чисел: Р = {0, 1, √2 , √3 , 2, √5, …} счетно, система прямоугольных чисел: P = áР,+,·,0,1ñ определена операциями сложения и умножения и двумя выделенными элементами (нулем и единицей). По отношению к сложению система P незамкнута. Множество неотрицательных целых чисел является подмножеством множества прямоугольных чисел. Для приведения (1) к виду уравнения Пифагора в системе прямоугольных чисел перепишем (1) как равенство для некоторых взаимно простых x’, y’, z’ и общего целого множителя d: (z’d)m = (x’d)p + (y’d)q и выполним масштабирование вниз:
(z’d)2 = (x’d)p / (z’d)m-2 + (y’d)q / (z’d)m-2 = (x’)p d p–m+2 / (z’)m–2 + (y’)q d q–m+2 / (z’)m–2 = xo2 + yo2 , где xo2 и yo2 с подходящим d - это квадраты некоторых прямоугольных чисел xo и yo. После масштабирования вверх возвращаемся к уравнению (1):
zm = xp + y q = (xp/m)m + (yq/m)m = zm–2 (xo2 + yo2) = xm + ym (2)
где xo и yo – целые прямоугольные числа по построению из уравнения (1), так как квадраты средних пропорциональных между xo2 и zm–2, yo2 и zm–2 - это целые числа xm, ym (для простоты записи в (2) обозначения для целых x, y оставлены прежними, хотя показатели p и q могут отличаться от m). Другими словами, xp/m и y q/m могут быть только целыми, потому что при иррациональных прямоугольных аргументах уравнение (2), не выполняется (подобные уравнения рассматривал еще Теэтет, живший до новой эры до Евклида) (см. аналогичные выкладки в [3]). Разные пары чисел (х,у) можно было бы выделить разным цветом, что очень важно для понимания качественной стороны дела, но для единообразия текста от этого пришлось отказаться.
Применим теперь древний метод построения степеней целых чисел, исходя из геометрической теоремы Евклида и записывая две цепочки пропорций, связанных между собой равенством z = k + l , где k и l – целые части z, получаемые из процедуры масштабирования вниз:
z/xo = xo/k = k/k1 = … = km–3 /km–2 (3)
z/yo = yo/l = l/l1 = … = lm–3 /lm–2
где z, xo , yo – прямоугольные числа из (2), m – натуральный индекс, не меньший 3, z = k + l , k и l - целые числа, полученные из скейлинга.
Из пропорций (3) можно получить следующие формулы:
xo2 = kz = (k1z /xo)z , xo3 = k1z2 = (k2z /xo)z2 , … , xom = km–2 zm–1, (4)
yo2 = lz = (l1z /yo)z , yo3 = l1z2 = (l2z /yo)z2 , … , yom = lm–2 zm–1,
где k и l находятся из предполагаемого равенства (1):
z = (z’d) = (x’d)p /(z’d)m–1 + (y’d)q /(z’d)m–1 = (x’)p d p-m+1/(z’)m–1 + (y’)q d q-m+1/(z’)m–1 = k + l
Если показатели p и q больше или равны m, тогда числа k и l будут целыми при d, кратном (z’)m–1 (d может быть очень большим целым числом, кратным также другим калибровочным множителям, выявляемым в процессе бесконечного спуска Ферма). Для получения примитивных пифагоровых троек в (2), необходимо провести калибровку (4). Покажем , как это можно было бы сделать. Итак, имеем:
z = (z’d) = (x’)p d p-m+1 /(z’)m–1 +(y’)q d q-m+1/(z’)m–1,
z2 = (z’d)2 = (x’)p d p-m+2 /(z’)m–2 + (y’)q d q-m+2 /(z’)m–2
После умножения z2 на калибровочный множитель (z’)m–2 получаем гипотетическую примитивную тройку Пифагора. Например, при p и q равных m получим примитивную тройку (z’)m/2, (x’)m/2, (y’)m/2 для уравнения: (z’)m = (x’)m + (y’)m .
Итак, из (2) и (4) получаем равные подобные разбиения zn на две целые части:
zm = xp + yq = zm–2(xo2 + yo2) = xm + ym (5)
где xo2 = (x’)p d p-m+2 /(z’)m–2, yo2 = (y’)q d q-m+2 /(z’)m–2 - это квадраты целых чисел, определяемые целыми x и y в (5). Другими словами, геометрическая структура уравнения (1) предопределяет пифагорову тройку чисел z , xo , yo для этого уравнения.
Квадратные корни из xm, ym являются средними пропорциональными между xo2 и zm–2, yo2 и zm–2 и описывают большой прямоугольный треугольник, определяемый скрытым пифагоровым равенством zm = xm + ym, находимым из соотношений: xm = k zm–1, ym = l zm–1, где k = xo2/z, l = yo2/z . Предполагаемый треугольник подобен треугольнику с целыми сторонами z , xo , yo .
Таким образом, обобщенное уравнение (1) сводится к гипотетическому уравнению с одинаковыми показателями степени при p, q ≥m (при p, q меньших m число z в уравнении (1) не может быть разбито на сумму натуральных чисел и уравнение (1) с целыми z, x, y не может существовать):
zm = xm + ym, m ≥3 (6)
с целыми x = x’d, y = y’d, z = z’d, и целым множителем d, который может быть разложен на произведение простых чисел. Теперь можно приступить к доказательству ВТФ и получить решение гипотезы Биля в полном объеме и единым способом.
Запишем теорему Ферма в ее обычной форме гипотетического равенства:
zn = xn + yn , n > 2 , x, y, z, n натуральные числа. (7)
Доказательство Обобщенной теоремы Ферма.
Предположим, что по крайней мере одно решение (7) существует. Тогда постараемся построить это решение и убедимся в его невозможности. Будем работать в системе прямоугольных чисел. Для того, чтобы получить степени целых чисел в (7), запишем две цепочки непрерывных пропорций, связанных между собой нормой прямоугольных чисел (см.[3]): z2 = x02 + y02 :
z/x0 = x0/k = k/k1 = … = kn–3 /kn–2
z/y0 = y0/l = l/l1 = … = ln–3/ln–2 (8)
где натуральные индексы последних термов каждой цепочки в (8) получаются из n > 2. Непрерывные пропорции в (8) дают следующие формулы:
z/x0 = x0/k = k/k1 = … = kn–3 /kn–2
z/y0 = y0/l = l/l1 = … = ln–3/ln–2
kz = x02, k1z = x0k, k2z = x0k1, …, kn-2z = x0kn-3 (9)
lz = y02, l1z = y0l, l2z = y0l1, …, ln-2z = y0ln-3
x02 = kz = (k1z /x0)z, x03 = k1z2 =(k2z /x0)z2, … , x0n = kn-2zn-1 (10)
y02 = lz = (l1z /y0)z, y03 = l1z2 =(l2z /y0)z2, … , y0n = ln-2zn-1
Теперь необходимо зафиксировать норму z для разбиения zn на две такие же степени в (7). Как и в случае гипотезы Биля, предположим, что z, x, y из равенства (7) имеют общий множитель d : z = (z’d), x = (x’d), y = (y’d), where z’, x’. y’ взаимно простые числа. После этого разделим равенство (7) на zn-1 и получим: z = (z’d) = (x’d)n /(z’d)n-1 + (y’d)n /(z’d)n-1 = k + l , где k и l целые, если d кратно (z’)n-1. После этого необходимо провести калибровку квадратов прямоугольных чисел с помощью подходящего d и модифицированных k и l : k = xo2/z, l = yo2/z . Отсюда и из (9)-(10) следует, что z2 = x02 + y02 и zn = zn-2 ( x02 + y02 ) как масштабированная модификация нормы z2 = x02 + y02 .
Далее можно получить единственное разбиение zn на три слагаемых из (10) для данной нормы при n > 2 :
zn = x0n + y0n + λn (11)
где λn = zn-1 [ (k – kn-2) + (l – ln-2) ] – остаток после вычитания x0n и y0n из zn, такой, что λn > 0 при n > 2 и x0 y0 ≠ 0, λn = 0 при n = 2 и x0 y0 ≠ 0 , x0 , y0 ∈ [0, z], z ∈ (0, ∞) .
Таким образом, имеется взаимно однозначное соответствие между каждой парой прямоугольных чисел (x0 , y0) с нормой z2 = x02 + y02 из 2- мерного арифметического пространства и каждым соответствующим разбиением любой целой степени с n > 2 целого числа z из n - мерного арифметического пространства на сумму таких же степеней чисел x0 , y0 с остаткомn из λ (11). Изоморфизм (взаимно однозначное соответствие) между множеством точек 2 – мерного евклидова пространства с вектором длиной z и координатами x0 , y0 , множеством разбиений z2 на квадраты прямоугольных чисел и множеством разбиений (11) для любого целого n > 2 может быть записан следующим образом:{z ⇒ (x0, y0) } ↔ { z2 = x02 + y02 }↔ { zn = x0n + y0n + λn}, где множества разбиений получаются из степенных подобий: z↔ z2 ↔zn , x0 ↔x02 ↔x0n , y0 ↔y02 ↔y0n .
Равенство (11) может быть сведено к норме, из которой оно было получено, тем самым предоставляя возможность для построения (7) из равных подобных разбиений:
zn = x0n + y0n + λn = zn-2 ( x02 + y02 ) = xn + yn (12)
Формула (12) представляет собой комбинаторное равенство двух разбиений на три и на два терма, вследствие взаимно однозначного соответствия между парами (x0 , y0) и предполагаемым разбиением (7). Это означает, что разбиение (7) строится в виде разбиения (11) из одних и тех же x0,, y0 . Для прямоугольных чисел это равенство может быть выполнено в предположении существования (7) только если x0, y0 целые. Алгоритм такого соответствия представлен формулой (13). Таким образом, масштабная инвариантность нормы z2 = ( x02 + y02 ) ведет к равенству между собой различных фрагментов разбиений (12):
x0n + y0n = ( xn or yn ) (13)
и соответственно λn = (yn or xn). Следует отметить, что x0n ≠ zn-2y02= yn и y0n ≠ zn-2x02 = xn из-за несовпадения разложений на простые множители для чисел x0n и yn, y0n и xn . Очевидно, что x0n ≠ zn-2•x02 и y0n ≠ zn-2•y02. Здесь также можно показать, что x0 and y0 не могут быть иррациональными в (13) из-за целого разбиения zn на xn и yn при n > 2 [3].
Вернемся теперь к предположению в начале доказательства о том, что целое решение (7) существует. Это предположение обосновано, только если существует конкретное решение (13) в целых числах. Для того, чтобы проверить справедливость (13), необходимо его построить с помощью тех же самых рассуждений, что и раньше, так как уравнения (7) и (13) одинаковы по своим свойствам. Эту процедуру можно выполнять до бесконечности в направлении уменьшения целых чисел при условии, что последовательность уменьшающихся равенств никогда не заканчивается и числа x02 и y02 в (12) всегда будут целыми. Если это было бы не так и числа x02 и y02 в цепочке равенств (13) оказались бы дробями, то значит решение (7) не существует в системе прямоугольных чисел, т.е. x, y, z в (7) не являлись бы целыми, что противоречит изначальной постановке задачи (основание степени z может быть разбито только на целые части по определению с одновременной калибровкой z2 на сумму целых квадратов x02 и y02) . С другой стороны, бесконечная последовательность зацепляющихся равенств (13) ведет к бесконечному уменьшению положительных целых чисел, что невозможно, и следовательно предположение о существовании целого решения (7) при n >2 не является истинным. Таким образом, теорема доказана как для всех четных, так и для всех нечетных степеней целых чисел для любых конечных целых x, y, z, d.
Выводы. Завершая доказательство Обобщенной теоремы Ферма, нужно сказать несколько слов о методе бесконечного спуска, который следовало бы отнести к метаматематическим методам. Действительно, по мере того, как в доказательстве появляются все меньшие и меньшие равенства (1), в масштабном множителе d обнаруживаются все новые и новые калибровочные факторы, Принципиальная разница здесь состоит в том, что d по определению конечно, хотя и неопределенно велико, а сам бесконечный спуск бесконечен, как следует из его названия. Таким образом, при конечных целых x, y, z, d бесконечный спуск не реализуется. Другими словами, цепочка зацепляющихся равенств (12) не приведет к спрямлению кривой Ферма (7) в целых числах, поскольку при суммировании линейных членов λn в целых числах в разбиении (7) по типу (11) доля целых степеней x0n и y0n в цепочке зацепляющихся равенств уменьшается, но никогда не исчезает полностью, что невозможно.
Итак, чему нас научила Великая теорема Ферма? Прежде всего, новой интерпретации целых чисел в общей системе наук и называемой нами квантовым подходом в прикладной и чистой математике [10]. Хотя название «квантовый» пришло из физики, основания квантовой математики коренятся в древних пифагорейских учениях и трудах древнегреческих математиков. Автору данной статьи удалось только прояснить понимание целых чисел как квадратов скрытых в их целостной природе прямоугольных чисел, образующих эффективную систему раскрытия внутренних свойств квантовых объектов. Геометрическое изображение математического кванта со структурой поверхностного фрактала [11], взятое из работы [6], дано в конце статье в виде Рис.1 (обозначения на рисунке объяснены в тексте статьи и в [6]). Таким образом, метаматематическое решение проблемы ВТФ оказалось возможным благодаря найденной системе прямоугольных чисел, составляющих основу квантовой математики.
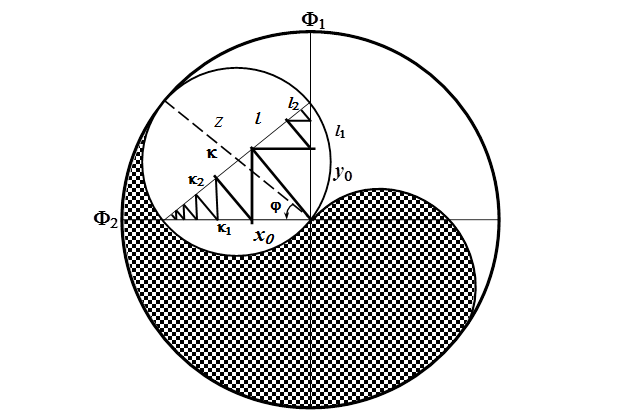
Рис. 1
Библиографическая ссылка
Ивлиев Ю.А. АЛЬТЕРНАТИВНОЕ ДОКАЗАТЕЛЬСТВО ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА КАК НАУЧНОЕ ОТКРЫТИЕ В МАТЕМАТИЧЕСКОЙ ПСИХОЛОГИИ // Научное обозрение. Фундаментальные и прикладные исследования. 2020. № 3. ;URL: https://scientificreview.ru/ru/article/view?id=89 (дата обращения: 27.01.2026).
DOI: https://doi.org/10.17513/srfar.89
