Введение
Современные вызовы для России требуют ответов на ряд принципиальных вопросов в аспекте новых реалий для решения приоритетов развития экономики страны: о месте России в мировой экономике и выборе пути и тенденций устойчивого развития в конкурентном мире в условиях многофакторных процессов и проблем многополярного мира по разным направлениям.
Но при решении этих общих задач в настоящее время возникла большая проблема/испытание с коронавирусом. Как оказалось – все это очень сильно связанные друг с другом сферы, которые надо решать в жесткой корреляции в рамках разумного протокола взаимодействия [1].
По оценке Председателя Счетной палаты А. Кудрина даже сейчас ясно, что экономика России просядет на 7% ВВП [2]. Но в этих условиях, когда экономические связи разных регионов нарушены, трудно ожидать устойчивости экономики. Однако, многие страны даже в этих непростых условиях быстро снимали ограничения на экономическую
деятельность [3]. Роспотребнадзор у нас был изначально вне этих тенденций с особым мнением без объективного обоснования, которое не может оспаривать даже губернатор на своей территории, и до сих пор продолжает перестраховываться со всякими условиями и с ожиданием новых волн пандемии [4].
В среднем в мире в 2018 г. на 1000 чел. населения приходилось около 13 (в России), 10 (в Италии) и 8 (в США) умерших человек [5]. Учет численности населения конкретной страны, – например Италии (порядка 50 млн. чел.), в которой начало пандемии получило большой общественный резонанс в Европе и всеобщую нестабильность, и последующего деления на 365 дней в году, приводит к оценке числа смертей в день (число погибших, подчеркиваем, а не зараженных). И это – долговременный процесс. Не правомерно говорить о трагических цифрах в аспекте жертв коронавируса – но это «обычная ситуация» с коррекцией для стандартной распространяющейся вирусной инфекции/эпидемии. В данном случае – почти все жертвы коронавируса в Италии имели другие серьезные проблемы со здоровьем [6].
Сравним со схожими историями развития эпидемий – см. в табл.1 [7].
Таблица 1. Данные по разным типам эпидемий. ТАСС, 2020.
Источник ФКУС РосНИПЧИ «Микроб» Роспотребнадзора.
|
Летальность |
Заболело |
Умерло |
Страны |
|
|
Птичий грипп 2003 |
53,0% |
861 |
455 |
17 |
|
Новый птичий грипп 2013-2018 |
39,0% |
1 568 |
615 |
3 |
|
Ближневосточный респираторный синдром 2012-н.в. Данные на 05.01.2020 |
35,6% |
2 535 |
921 |
27 |
|
Атипичная пневмония 2002-2003 |
9,6% |
8 096 |
774 |
32 |
|
Коронавирус 2019-н.в. Данные на 11.03.2020 |
3,4% |
119 303 |
4 290 |
115 |
|
Свиной грипп 2009-2010 |
0,2% |
Нет данных* |
18 499 |
214 |
*С августа 2009 года подсчет случаев прекращен из-за невозможности отследить все случаи заражения
О причинах возникновения пандемии существуют разные мнения, в том числе и предположения о вышедшей из-под контроля/самопроизвольной утечке разработанного бактериологического оружия, да еще с заложенным алгоритмом непрерывной трансформации вируса через фиксированное время (см. например [8]). Судя по быстрой, беспрецедентной, начальной реакции Китая, США – это возможно, и здесь возникает много вопросов, но глобальную мировую проблему создать удалось. ВОЗ в этой ситуации показал свою некомпетентность и отсутствие прогнозных технологий для вырабатываемых рекомендаций, часто противоречивых друг другу в разные дни.
Для России приведенные выше цифры по умершим в обычные годы соответствуют более 5000 смертей в день. За 3 месяца пандемии в России погибло такое же количество людей (данные за 15.06.2020) [9]. Но при тотальном освобождении больниц от «обычных» больных в пользу ожидаемого наплыва «коронавирусных» пациентов, первые же никуда не делись, однако перестали относиться к приоритетам оказания помощи [10]. Тогда трудно говорить о статистически обоснованной демографически-экономической оценке ситуации и качестве жизни населения в отсутствие элементарного права на медпомощь в условиях страховой медицины с ее огромными финансовыми средствами. Но ведь и в «обычные времена» больницы были переполнены, и была огромная нехватка первичного медперсонала в последние годы [11]. Cейчас это пытаются исправить, хотя парадокс заключается в том, что больничное руководство и не очень-то в этом заинтересовано экономически – они могут лишаться экстремальных бюджетных денежных средств, выделяемых адресно под коронавирус.
В данной нашей статье делается попытка провести анализ на основе базовых принципов (Раздел 1) и определенной модели динамического процесса (Раздел 2) – ср. с [12]. В Разделе 3 обсуждаются вероятностные модели перехода между возможными состояниями в экономической системе с устойчивыми режимами распространения определенного признака. Речь идет о некоторых особенностях протокола взаимодействия медицины и экономики с обоснованием некой стратегии действий в предшествующей и нынешней ситуации на принципах простой рекомендации – вернуться к нормальным экономическим отношениям в России. В первую очередь, это касается высокотехнологических секторов промышленности, для которых в условиях эпидемии можно временно работать «на склад», а не непосредственно на «замороженный» рынок (см. например [13,14]). В Заключении даются некоторые возможные рекомендации по результатам проведенного моделирования при принятии управленческих решений.
1. Базовые принципы – устойчивость экономики в форматах офисной on-line е-активности и добывающих и/или обрабатывающих отраслей
Первый вопрос, который требует обсуждения – on-line технологии и опосредованные контакты в науке и образовании, при которых, очевидно, происходит приостановка работ по прорывным технологиям и новому производству, по научному поиску в высокотехнологичных секторах промышленности (конкурентных непроизводственной ИКТ-индустрии). Не надо забывать и об утечке информации через такие on-line технологии как в аспекте know-how и производственных секретов, так и в аспекте вопросов национальной безопасности.
Отдельное направление рисков и угроз – возникающие масштабы кибермошенничества и злоупотреблений вокруг всей этой on-line индустрии и создаваемой инфраструктуры. Данный сегмент – большие объемы прямого экономического ущерба как для отдельных граждан, так и для государства в целом, а также для задач национальной безопасности в условиях утечек информации из-за несовершенства и ненадежности информационных сетей массового пользования из разных незащищенных on-line бытовых точек коммуникаций (см. напр. [15]).
Стоит еще раз прислушаться к главе Счетной палаты Алексею Кудрину, который определенно считает, что потери экономики России от коронавируса составят заметный процент ВВП. При этом он не исключает и более пессимистичного развития экономической ситуации в стране [16].
В США и ряде других стран реализуется другая – прагматичная и компромиссная – модель, когда не был введен жесткий карантин в связи с распространением коронавируса. По официальным данным в этих странах регистрируются немалые случаи заражения [17-19], но доминанта проблемы связывается с будущим местом экономики этих стран в мире после эпидемии. При этом все ограничения, в разных странах носили, в основном, рекомендательный характер.
Единственное, что известно на сегодняшний день в формате доказательной
медицины — это ослабление иммунитета у заразившегося, а дальше — у каждого по-разному, в зависимости от состояния его здоровья; и возраст здесь далеко не самое главное как и в СПИДе/AIDS. Несмотря на колоссальное число больных у нас, реакция общества в этом случае является вполне толерантной: ни тотальной изоляции, ни тотального строительства больниц с соответствующим оборудованием. По словам главы Счетной палаты, вирус иммунодефицита представляет для России более серьезную угрозу, чем коронавирус: по официальным данным в стране живут 1 млн. человек с ВИЧ [20]. Но тем не менее, ЧС не обозначивается.
Очевидно, что на все это надо смотреть в комплексе — здоровье человека и психологическое состояние граждан (и не по одной болезни), состояние общества в целом и его социально-ориентированные приоритеты на деле, экономическая ситуация в стране (в т.ч. на перспективу — после эпидемии – все службы сервиса, заводы и фабрики мгновенно не восстановятся), компетентность и профессионализм властей на разных уровнях и их способность принимать взвешенные решения. Это требует анализа, моделирования и прогнозирования, в том числе и исходя из исторического опыта.
К сожалению, несмотря на жесткие меры карантина в России, здесь много вопросов: за сутки регулярно фиксируется значительное число заболевших и рост смертности (см. например рекордные данные за 11.05.2020 [21], и текущие цифры так называемого «плато» не безупречны [22]), а также трудно объяснимую причину заболевания на высоком государственном уровне [23]. Все это постоянный, по-видимому, фактор. С его учетом и надо выстраивать социально-экономические ориентиры в стране.
В следующем разделе 2 мы попытаемся продемонстрировать, как с помощью математического моделирования и компьютерной симуляции можно разработать обоснованный ландшафт возможной деятельности соответствующих госслужб при эпидемии. Это основывается на результатах предсказательного моделирования развития сложной ситуации в условиях многофакторного динамического процесса с учетом необходимости сохранения стабильности экономики при работе людей на своих привычных местах с естественными рекомендательными ограничениями.
2. Моделирование распространения коронавирусной инфекции методом клеточных автоматов в инфекционной/генетической модели
Рассмотрим агент-ориентированный подход SIR [24], который оперирует с населением/популяцией на отдельной территории, на которой распространяется инфекция: население делится на 3 класса: S(t) — восприимчивые к инфекции (уязвимые), но еще не зараженные люди в текущий момент времени t; I(t) — зараженные индивиды, способные передавать инфекцию восприимчивым к ней лицам; R(t) — вылечившиеся и приобретшие иммунитет к данному заболеванию, неспособные более заболеть и/или передать инфекцию, с очевидным условием S(t)+I(t)+R(t)=const=N, где N – число индивидов на данной территории. При этом ключевыми параметрами являются: β – представляет собой частоту контактов (вероятность того, что кто-то заразится этой болезнью при контакте с кем-то, кто болен) и γ – скорость восстановления, которая показывает, насколько быстро люди выздоравливают (и становятся иммунными). Решение соответствующей системы уравнений по методу клеточного автомата, описывающей динамику этих трех обозначенных классов (мы его для краткости не приводим – см. [12,14,25]), обеспечивает временной ход и наглядную пространственную оценку процесса распространения эпидемии. Мы сфокусируем свое исследование только на общих тенденциях и ключевых параметрах. Хотя, такой принципиальный фактор как тяжесть болезни в данной простой модели не учитывается, но, в принципе, это можно сделать с дополнительным введением соответствующих весовых коэффициентов в усовершенствованные параметры задачи.
Предложенная модель была реализована с параметрами, характерными для коронавирусной инфекции для случая начального экспоненциального ее роста, присущего пандемии. Расчет основывается на продолжительности протекания болезни (например, по имеющейся практике – 22 дня) и базового репродуктивного коэффициента R0 (скорость распространения инфекции) – R0=2.5. Тогда имеем в относительных единицах для обозначенных выше параметров: β=0.1125, γ≈0.045 (ср. с [26]). При этом, для крайне заразных заболеваний β стремится к 1, а γ – к 0.
На рис.1 приведены результаты моделирования процесса распространения эпидемии (в относительных единицах) на территории с указанными выше параметрами, где для определенности задачи в качестве начальных условий задавалось случайное распределение в пространстве (на территории) восприимчивых индивидов (на примере первых дней распространения инфекции в виртуальном городе с количеством населения порядка его значения для г. Москва, находящегося в данный момент в контактом состоянии):
11.9 млн человек (отмечено красным цветом на рис 1а), с числом уже зараженных людей – 50646 человек (зеленый цвет), иммунных по разным причинам индивидов – полагаем 30% от населения, а также уже переболевших/выздоровевших – 4610 человек (синий цвет). Указанные параметры соответствовали статистике распространения коронавирусной инфекции в г. Москва на 29.04.2020 [27]. При этом оценивался маршрут (рис. 1г) распространения инфекции с градацией по каждым двум соседним пунктам – отмечены точками, с учетом потока возможных заболевших в относительных единицах.
Анализируя проведенные расчеты, можно заключить, что в начале процесса – с 1-ый по 20-ый день от исходного появления инфекции – наблюдается быстрое ее распространение с уменьшением восприимчивых индивидов до нуля при совпадении количества зараженных и переболевших-иммунных людей; к 30-му дню прослеживается уменьшение заболевших людей в два раза, пик заболеваемости считается пройденным и наблюдается явная тенденция к окончанию эпидемии; а затем, спустя 171 - 180 дней, вся популяция перейдет в группу иммунных (все выздоровели), и распространение инфекции можно считать закончившимся.
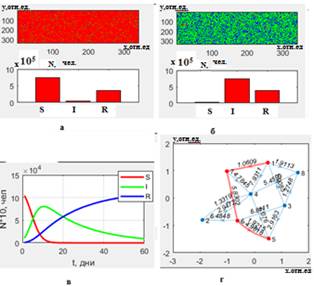
Рис. 1. Начальное пространственное распределение модели SIR в относительных единицах (а); распределение SIR после 14 дней эпидемии (б); динамика изменения численности людей в классах S,I, R за 60 дней (в); маршрут распространения инфекции на случайном графе между фиксированными соседними территориями (они отмечены цифрами 1-7) из-за, например, транспортных потоков (г). Внизу рисунков а,б показаны гистограммы для разных классов населения. Координаты х, у по осям показывают размеры исследуемой территории на плоскости.
На основе результатов моделирования, в рамках модели графов [28], можно сделать заключение о неоднозначности мер по ограничению контактов и самоизоляции в целях контроля распространения коронавирусной инфекции, поскольку рост числа заболевших людей становится субэкспоненциальным при любом начальном распределении числа контактирующих людей, находящихся в потенциальном риске заразиться. Только после этого можно говорить о стабилизации эпидемиологического процесса. Этот факт насыщения признака является универсальным для любой нелинейной динамической системы с потерями при ограниченности ее ресурсов [29].
Другие результаты моделирования продемонстрированы на рис. 2-6, включая территориальные связи.
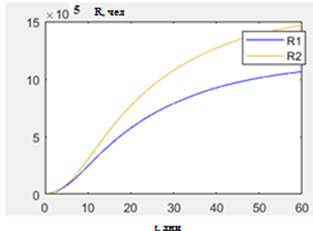
Рис.2. Число переболевших людей от времени при различных значениях численности населения: R1 при 16 млн населения, R2 при 11.9 млн населения.
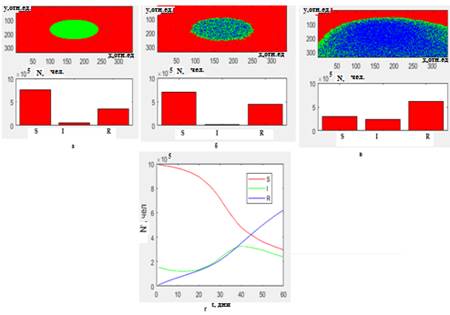
Рис. 3. Распространение эпидемии из изолированного центра с соответствующим гистограммами: начальное распределение модели SIR (а); распределение SIR после 14 дней (б) и 60 дней (в); динамика изменения численности людей в классах S,I, R за 60 дней (г).
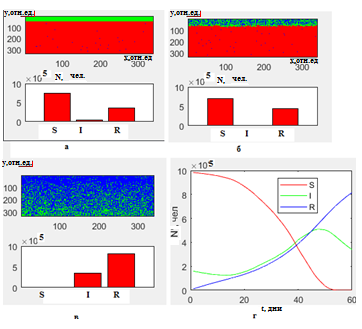
Рис. 4. Распространение эпидемии от верхней границы для соседних территорий с соответствующими гистограммами: начальное распределение модели SIR (а); распределение SIR после 14 дней эпидемии (б) и 60 дней (в); динамика изменения численности людей в классах S,I, R за 60 дней (г).
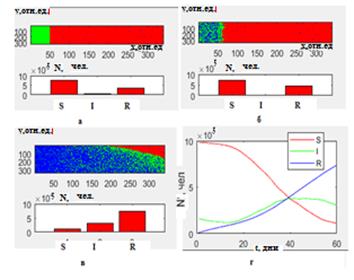
Рис. 5. Распространение эпидемии от левой границы для соседних территорий с соответствующими гистограммами: начальное распределение модели SIR (а); распределение SIR после 14 дней (б) и 60 дней (в); динамика изменения численности людей в группах S,I, R за 60 дней (г).
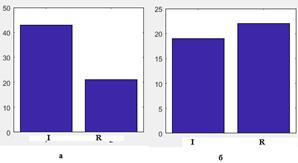
Рис 6. Число людей (N) в классах I и R после 2-го дня заражения при R0=2.5 (а) и
R0= 1.5 (б).
3. Медицина и экономика – новый протокол взаимодействия
Взаимоотношения между двумя сегментами – медициной и экономикой – должны базироваться на разумном компромиссе в формате «здоровье людей-их экономическое положение». На этом пути, по-видимому, в том числе и по уже имеющемуся опыту пандемии за последние месяцы, можно сформулировать некоторые возможные рекомендации для принятия управленческих решений в едином комплексе развития ситуации по разным критериям с просчетом экономических последствий их реализации. Здесь полезными могут быть вероятностные подходы и модели для перехода между разными состояниями с выбором определенных режимов для реализации конечных устойчивых состояний.
Для процессов диффузионного типа базовым уравнением является соответствующее дифференциальное кинетическое уравнение для вероятности W(y2|y1) перехода из начального состояния y1 в конечное состояние y2 за единичное время на множестве событий Y [30,31]. В нашем случае эти состояния можно связать либо с развитием эпидемии, либо с инновационным процессом перехода от выпуска стандартной продукции y1 к инновационной y2 за определённое время t, т.е. Wt(y2|y1)≥0.
В простейшем случае − на начальном, обычно затратном, этапе – это одномерный/однонаправленный волновой процесс: с интенсивностью/амплитудой определенного признака/параметра u(t,x), изменяющегося во времени (t) и в конфигурационном пространстве (x) с фиксированным темпом/скоростью v изменения x, что и определяет скорость изменения самого признака. Такой процесс описывается хорошо известным волновым уравнением с периодическими решениями во времени и по пространству [29].
Но мы сразу обратимся к модели нелинейного процесса и для краткости приведем только конечные результаты моделирования. Они представлены на рис. 7 при решении базового уравнения (в нелинейной теории волн оно носит название уравнения
Кортевега – де Вриза с солитонного типа решениями [32,33]).
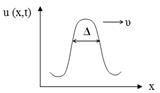
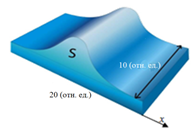
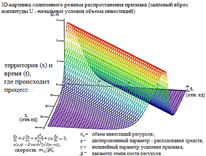
Рис.7. Солитонный характер решений – схематическое изображение при разных размерностях объекта. Параметры указаны на рисунке справа для численного 3D-анализа (триггерный/flash процесс распространения).
Профиль такого волнового объекта представляет собой возмущение колоколообразной формы с некоторой максимальной амплитудой u (которая может определять и объем финансирования/ инвестиций), не изменяющейся по форме со временем для разных x – устойчивый сценарий развития динамического процесса по признаку u.
Следствием такого решения является факт, что скорость движения v солитона/признака (финансового потока, например) прямо пропорциональна амплитуде (по объему средств) солитона (v ~ u), а его «ширина» Δ – обратно пропорциональна корню квадратному из амплитуды, т.е. скорости/темпу изменения переменной x, определяющей скорость v 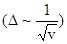 .
.
Данный факт имеет принципиальное значение для состояния солитона и определяет при таком моделировании функционирование экономической системы и/или распространение эпидемии как устойчивого/когерентного динамического процесса/объекта до определенного/управляемого внешнего воздействия через соответствующие критические параметры. Это и дает основу для принятия оптимального управленческого решения. Главная проблема здесь – нахождение значений этих критических параметров для реальных условий.
Заключение
В связи с продолжающейся опасностью эпидемии COVID-19 и, возможно, будущими ее волнами, необходимо рассмотреть дальнейшее усовершенствование используемых моделей в едином медико-экономическом и инфраструктурном аспектах с перезагрузкой приоритетов развития экономики России с соответствующими новыми экономическими ориентирами. Данные исследования необходимо продолжать, поскольку в настоящее время наблюдается определенный оптимизм в исчезновении коронавируса, пока еще ни на чем объективном не основанный, как и, впрочем, предшествующие драматические негативные выводы [34,35]. При этом необходимо оценивать распространение эпидемии и ее экономические последствия, в абсолютных (а не относительных) единицах для управляющих параметров динамической модели. Здесь возможны и фрактальные всплески, которые требуют также проверки на устойчивость в том числе, и с пространственным подобием развития очагов эпидемии на разных территориях. Поэтому экономическая жизнь в стране должна быть устроена с учетом данного обстоятельства (ср. с [36,37]), но в приоритете – с прорывом в наукоемких технологиях на отечественных достижениях (ср. с [13,14].
Однако, тотальное падение машиностроительной отрасли в стране за многие годы, как гаранта ее самодостаточности и развития России по всем другим направлениям, не обсуждается как доминанта. Из объявленных особо нуждающихся в помощи государства отраслей нет абсолютного приоритета промышленности и сервиса вокруг нее [38] (ср. с [39]).
Именно для решения этой проблемы в аспекте новой промышленной политики и трансфера технологий в задачах отраслевого импортозамещения нужен научно-обоснованный прогноз развития обрабатывающей промышленности России в экстремальных и неожиданных условиях типа нынешней пандемии.
В заключение один принципиальный урок пандемии. Сейчас уже признано на многих уровнях, что относительно «мягкий» процесс пандемии в России по сравнению с другими странами мира связан с сохранением основ советского формата санитарно-эпидемиологических служб практически на всех территориях страны [40]. Не будем продолжать далее, что еще было эффективно в СССР, но в нынешних реалиях развитие возможно на путях отечественного государственно-частного партнерства по стратегическим направлениям экономики при движении по траектории создания истинно социально-ориентированного государства [41].
Библиографическая ссылка
Бухаров Д.Н., Трифонова Т.А., Аракелян С.М. МОДЕЛИРОВАНИЕ ПРОЦЕССА РАСПРОСТРАНЕНИЯ COVID-19 – СИГНАЛ ДЛЯ ПЕРЕЗАГРУЗКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ОРИЕНТИРОВ РОССИИ // Научное обозрение. Фундаментальные и прикладные исследования. 2020. № 4. ;URL: https://scientificreview.ru/ru/article/view?id=90 (дата обращения: 01.03.2026).
DOI: https://doi.org/10.17513/srfar.90
