Введение
В работе проводится обзор способов умножения, с дополнениями, произведений двух сомножителей, первый из которых состоит из однородных цифр, главном образом, девяток в произвольном количестве, как наиболее удобных для выполнения торговых и других расчетов. Второй сомножитель при этом может состоять из различного количества произвольных цифр. Девяткой можно воспользоваться и в случаях, когда первый сомножитель состоит из других однородных цифр.
Цель работы
Целью работы является определение вариантов более простых способов нахождения ответов указанных произведений первых сомножителей на двучлены, трехчлены и так далее, и некоторых других вариантов произведений.
Результаты исследований и их обсуждение
Напомним структуру произведений, изложенную в [1-2]. Количество цифр первого сомножителя обозначим 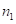 , второго
, второго 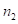 . Ответ произведения, в общем случае, состоит из трех частей: 1-ой (начальной), 2-ой (средней), 3-ей (последней). Наиболее консервативная 3-я часть ответа; в 1-ой при определённых обстоятельствах может измениться последняя цифра. Первая и третья части ответа состоят из одинакового количества цифр, равного их количеству в наименьшем из сомножителей. Средняя, т.е. 2-ая часть, наиболее вариабельная. Она состоит из периодических цифр в количестве
. Ответ произведения, в общем случае, состоит из трех частей: 1-ой (начальной), 2-ой (средней), 3-ей (последней). Наиболее консервативная 3-я часть ответа; в 1-ой при определённых обстоятельствах может измениться последняя цифра. Первая и третья части ответа состоят из одинакового количества цифр, равного их количеству в наименьшем из сомножителей. Средняя, т.е. 2-ая часть, наиболее вариабельная. Она состоит из периодических цифр в количестве 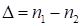 , при
, при 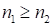 или из периодических цифр в количестве
или из периодических цифр в количестве 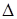 , последняя цифра из которых на единицу меньше (т.е. имеет место сбой в ответе). В этом случае последняя цифра первой части ответа увеличивается на единицу.
, последняя цифра из которых на единицу меньше (т.е. имеет место сбой в ответе). В этом случае последняя цифра первой части ответа увеличивается на единицу.
Замечание 1. Общее количество цифр в ответе равно сумме их в обоих сомножителях.
Замечание 2. Если цифры 1-го сомножителя состоят из девяток, то средняя часть ответа состоит только из периодических девяток в количестве равным 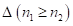 . Случаи, когда
. Случаи, когда 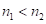 рассмотрены по ходу применения их в работе [2].
рассмотрены по ходу применения их в работе [2].
Особенностью ответа всех произведений 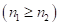 является равенство суммы величин 1-ой и 3-ей частей их средней части ответа, состоящей из такого же количества цифр, если даже их нет в реальном ответе. В этом случае 2-ую часть называют средним числом. Если известны две какие-либо части ответа, всегда можно найти 3-ью. Периодическое число 2-ой части, может быть найдено независимо от 1-ой и 3-ей частей ответа, путем сведения к “простому” (коренному, одной цифре) числу произведения суммы цифр 2-го сомножителя на цифру 1-го. Если средняя часть ответа, состоящая из этих периодических чисел в количестве равном 1-ой или 3-ей части, окажется меньше какой-либо из них, то в ответе имеем сбой.
является равенство суммы величин 1-ой и 3-ей частей их средней части ответа, состоящей из такого же количества цифр, если даже их нет в реальном ответе. В этом случае 2-ую часть называют средним числом. Если известны две какие-либо части ответа, всегда можно найти 3-ью. Периодическое число 2-ой части, может быть найдено независимо от 1-ой и 3-ей частей ответа, путем сведения к “простому” (коренному, одной цифре) числу произведения суммы цифр 2-го сомножителя на цифру 1-го. Если средняя часть ответа, состоящая из этих периодических чисел в количестве равном 1-ой или 3-ей части, окажется меньше какой-либо из них, то в ответе имеем сбой.
1 Приведем методы умножения первых сомножителей, составленных из девяток.
1. Общий универсальный метод для всех разновидностей 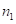 и
и 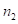 , использующий таблицу умножения [1].
, использующий таблицу умножения [1].
2. Метод “зануления” девяток (общеизвестный, [1]). Пример: 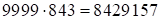 . Получаем: a)
. Получаем: a) 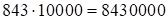 ; б)
; б) 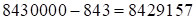 .
.
Здесь 842 – 1-ая часть ответа, 9 – 2-ая часть, а второе число средней части 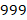 ; 3-я часть – 157. Все – 1-ая, 3-я части и 2-ое число (виртуальная, [3]) – трехчлены, т.к.
; 3-я часть – 157. Все – 1-ая, 3-я части и 2-ое число (виртуальная, [3]) – трехчлены, т.к. 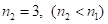 . Вторая часть – 9, т.к.
. Вторая часть – 9, т.к. 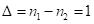 .
.
3. Пример: 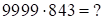
Метод произведения соответствующих цифр обоих сомножителей
(метод “скобок” – 1, [2]). Перемножая, получим: 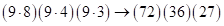 . Затем справа налево суммируем соседние цифры скобок в количествах
. Затем справа налево суммируем соседние цифры скобок в количествах 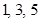 , а затем т.к.
, а затем т.к. 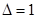 , суммируем один раз все цифры, а далее слева направо в количествах
, суммируем один раз все цифры, а далее слева направо в количествах 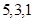 (аналогично поступаем в подобных случаях в дальнейшем).
(аналогично поступаем в подобных случаях в дальнейшем).
1) 7 ; 2) 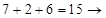 5 ?; 3)
5 ?; 3) 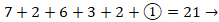 1 ?; 4)
1 ?; 4) 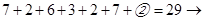 9 ?; 5)
9 ?; 5) 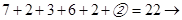 2 ?; 6)
2 ?; 6) 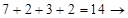 4 ?; 7)
4 ?; 7) 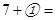 8
8
С конца (в обратном порядке) записываем цифры в квадратах (здесь и далее). Получим 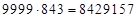 .
.
Замечание: индексы (цифры в кружочках) прибавляем к последующим суммам цифр (здесь и далее).
4. Метод пошагового суммирования (метод “скобок” – 2, 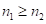 ). [2]
). [2]
Примеры:
а) 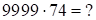
Перемножаем, смещая двучлен пошагово налево до совпадения первых цифр сомножителей следующим образом:
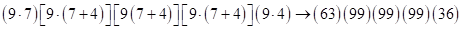 – пошагово суммируем справа налево, получаем: 1) 6 ; 2)
– пошагово суммируем справа налево, получаем: 1) 6 ; 2) 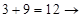 2 ?; 3)
2 ?; 3) 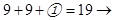 9 ?;
9 ?;
4) 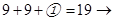 9 ?; 5)
9 ?; 5) 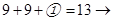 3 ?; 6)
3 ?; 6) 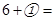 7
7
Ответ: 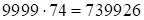 .
.
б) 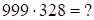
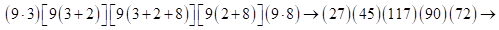 переходим к двучленам в каждой скобке, прибавляя сотни к десяткам предыдущей скобки
переходим к двучленам в каждой скобке, прибавляя сотни к десяткам предыдущей скобки 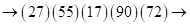 пошагово суммируем справа налево, десятки каждой скобки с единицами соседней левой скобки
пошагово суммируем справа налево, десятки каждой скобки с единицами соседней левой скобки 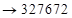 .
.
Ответ: 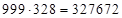 .
.
5. Умножение “столбиком” (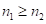 ), [2]. Примеры:
), [2]. Примеры:
а) 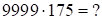
Сначала записываем произведения крайних цифр сомножителей (в виде двучленов), затем суммы цифр крайних двучленов, второго сомножителя умноженные на 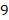 , и складываем их следующим образом:
, и складываем их следующим образом:
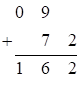 и
и 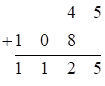 , где
, где 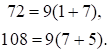
Т.к. количество цифр в каждой части равно 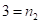 , то старшая цифра второй суммы (единица) прибавляется к единицам первой. Получаем
, то старшая цифра второй суммы (единица) прибавляется к единицам первой. Получаем 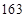 и
и 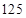 – 1-ая и 3-я части произведения, затем произведение
– 1-ая и 3-я части произведения, затем произведение 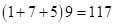 располагаем между трехчленами 1-ой и 3-ей части и распределяем
располагаем между трехчленами 1-ой и 3-ей части и распределяем  между ними:
между ними:
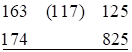 , где
, где 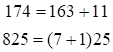
т.е. единицы прибавляем к старшему разряду правой части ответа (3-ей), а остальные цифры 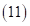 к соответствующим разрядам первой части. Но в примере
к соответствующим разрядам первой части. Но в примере 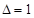 , следовательно, существует средняя часть ответа в виде одной цифры. В случае первого сомножителя, состоящего из девяток, вторая часть ответа –
, следовательно, существует средняя часть ответа в виде одной цифры. В случае первого сомножителя, состоящего из девяток, вторая часть ответа – 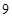 . Проверим:
. Проверим: 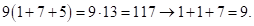 Итак, ответ:
Итак, ответ: 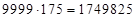 .
.
б) 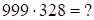
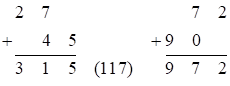 , где
, где 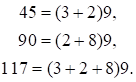 далее
далее 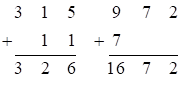
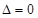 , средней части нет. Ответ:
, средней части нет. Ответ: 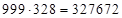 .
.
6. Самый простой способ умножения первого сомножителя, состоящего из девяток на произвольный второй сомножитель для случая 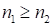 , [2].
, [2].
Суть способа: сразу записываем части ответа, первая часть – это второй сомножитель, уменьшенный на единицу, третья часть – разность между второй (виртуальной) частью, состоящей из девяток в количестве 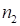 и первой частью ответа. Вторая часть ответа состоит из девяток в количестве
и первой частью ответа. Вторая часть ответа состоит из девяток в количестве 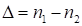 .
.
Пример: 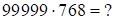 . Ответ:
. Ответ: 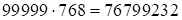 , где
, где 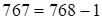 – первая часть ответа,
– первая часть ответа, 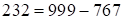 – третья часть ответа,
– третья часть ответа, 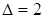 , следовательно, средняя часть ответа 99.
, следовательно, средняя часть ответа 99.
Замечание: для случая 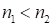 , первая и третья часть ответа находятся несколько иначе. Первая и третья часть ответа по количеству цифр равны
, первая и третья часть ответа находятся несколько иначе. Первая и третья часть ответа по количеству цифр равны 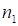 , только первая часть – это первые числа второго сомножителя, причем последняя цифра на единицу меньше. Третья часть – это разность между числом, состоящим из девяток в количестве
, только первая часть – это первые числа второго сомножителя, причем последняя цифра на единицу меньше. Третья часть – это разность между числом, состоящим из девяток в количестве 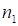 и количеством последних цифр второго сомножителя, уменьшенных на единицу. Между ними располагается средняя часть ответа. Она находится как сумма последних цифр второго сомножителя в количестве
и количеством последних цифр второго сомножителя, уменьшенных на единицу. Между ними располагается средняя часть ответа. Она находится как сумма последних цифр второго сомножителя в количестве 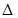 и разности между числом девяток и первых цифр второго сомножителя.
и разности между числом девяток и первых цифр второго сомножителя.
Рассмотрим на примере (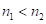 ):
): 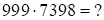
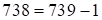 – первая часть ответа,
– первая часть ответа, 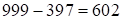 – третья часть ответа, так как
– третья часть ответа, так как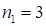 . Средняя часть:
. Средняя часть: 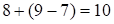 , так как
, так как 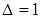 . Получим
. Получим 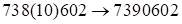 , так как
, так как 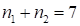 . Итак, ответ:
. Итак, ответ: 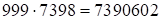 .
.
7. Добавим еще один способ умножения первого сомножителя, состоящего из девяток на любой второй сомножитель для случая 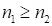 и
и 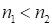 . Это способ “разделения на десятки и единицы”.
. Это способ “разделения на десятки и единицы”.
В этом случае каждую цифру второго сомножителя умножаем на 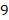 и записываем последовательно десятки произведения слева, а соответствующие единицы справа. Затем при
и записываем последовательно десятки произведения слева, а соответствующие единицы справа. Затем при 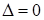 от каждой цифры правой части (единиц), кроме последней, отнимается единица и прибавляется к советующим десяткам левой части (кроме последней цифры десятков).
от каждой цифры правой части (единиц), кроме последней, отнимается единица и прибавляется к советующим десяткам левой части (кроме последней цифры десятков).
Примеры (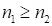 ):
):
а) 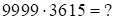
1) 2504 – десятки, 7495 – единицы;
2) 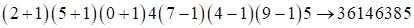 ,
, 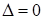 , следовательно, средней части в ответе нет. Итак, ответ:
, следовательно, средней части в ответе нет. Итак, ответ: 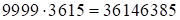 .
.
б) 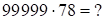 Найдем первую и третью части ответа
Найдем первую и третью части ответа
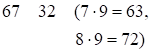
Последние цифры произведения 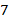 и
и 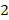 – неизменны, а первые
– неизменны, а первые 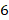 и
и 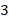 изменяются на единицу: первая (десятки) увеличивается, вторая (единицы) – уменьшается. Получаем
изменяются на единицу: первая (десятки) увеличивается, вторая (единицы) – уменьшается. Получаем 
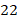 . Так как
. Так как 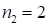 , где
, где  – первая часть ответа, а
– первая часть ответа, а 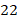 – третья. Вторая часть ответа состоит из девяток в количестве
– третья. Вторая часть ответа состоит из девяток в количестве 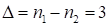 , т.е. равна
, т.е. равна 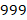 . Итак, ответ:
. Итак, ответ: 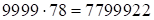 .
.
Случаи, когда 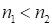 . В этом случае первая и третья части ответов – крайние цифры у десяток (слева) и единиц (справа) соответственно. Каждая из них содержит количество цифр, равное их количеству в меньшем сомножителе. Без изменения остаются последние цифры, остальные изменяются на единицу, как ранее указано. Средняя часть есть сумма оставшихся цифр в количестве, равном меньшему сомножителю.
. В этом случае первая и третья части ответов – крайние цифры у десяток (слева) и единиц (справа) соответственно. Каждая из них содержит количество цифр, равное их количеству в меньшем сомножителе. Без изменения остаются последние цифры, остальные изменяются на единицу, как ранее указано. Средняя часть есть сумма оставшихся цифр в количестве, равном меньшему сомножителю.
Примеры:
а) 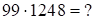
Решение: перемножаем и разделяем соответствующие десятки и единицы. Получим 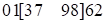 . За квадратными скобками цифры первой и третей части – двучлены. Т.к.
. За квадратными скобками цифры первой и третей части – двучлены. Т.к. 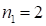 , то их последние цифры неизменны, а предыдущие изменяются на единицу, т.е.
, то их последние цифры неизменны, а предыдущие изменяются на единицу, т.е. 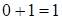 ; а
; а 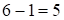 получим:
получим: 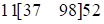 . Средняя часть есть сумма оставшихся двучленов (в скобках), т.е.
. Средняя часть есть сумма оставшихся двучленов (в скобках), т.е. 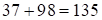 . Получили
. Получили 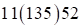 , но
, но 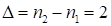 , следовательно, в ответе должно быть
, следовательно, в ответе должно быть 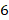 цифр. Первую цифру скобки прибавляем к единицам первой части. Получим ответ:
цифр. Первую цифру скобки прибавляем к единицам первой части. Получим ответ: 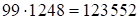 .
.
б) 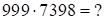
Решение: умножаем и отделяем первую и третью части 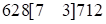 , первая и третья части ответа – трехчлены, т.к.
, первая и третья части ответа – трехчлены, т.к. 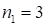 (вне скобок). Следовательно, две первые цифры первой части увеличиваются на единицу, а две первые цифры третьей части уменьшаются на единицу, третьи их последние цифры – без перемен. Получим
(вне скобок). Следовательно, две первые цифры первой части увеличиваются на единицу, а две первые цифры третьей части уменьшаются на единицу, третьи их последние цифры – без перемен. Получим 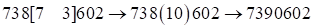 . Итак, ответ:
. Итак, ответ: 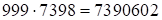 .
.
в) 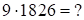
Решение: 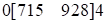 . Здесь первая и третья части – однозначные, следовательно, остаются без перемен. Среднюю часть находим как сумму трехчленов в скобках по разрядам. Получим
. Здесь первая и третья части – однозначные, следовательно, остаются без перемен. Среднюю часть находим как сумму трехчленов в скобках по разрядам. Получим 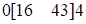 , а т.к.
, а т.к. 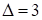 , то имеем
, то имеем 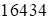 , где
, где 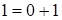 . Итак, ответ:
. Итак, ответ: 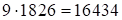 .
.
Замечание: способ разделения десяток и единиц (способ 7) можно применять для нахождения ответа произведения второго сомножителя на любое однозначное число первого сомножителя.
Пример: 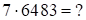
Решение: 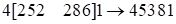 , где
, где 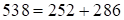 .
.
Ответ: 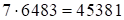 .
.
Отметим, что из всех приведенных способов умножения, способы 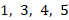 могут использоваться также, если первый сомножитель состоит из других однородных цифр.
могут использоваться также, если первый сомножитель состоит из других однородных цифр.
Примеры:
а) метод 3: 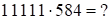
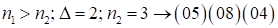 . Суммируем справа налево цифры в количествах
. Суммируем справа налево цифры в количествах 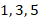 , а затем для получения средней части суммируем дважды по шесть цифр т.к.
, а затем для получения средней части суммируем дважды по шесть цифр т.к. 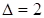 , а затем слева направо – цифры в количестве
, а затем слева направо – цифры в количестве 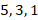 . Везде с учетом индексов.
. Везде с учетом индексов.
Получим: 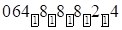 . Итак, ответ:
. Итак, ответ: 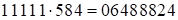 . Ноль добавлен впереди для формализации ответа, т.к. количество цифр в ответе должно равняется
. Ноль добавлен впереди для формализации ответа, т.к. количество цифр в ответе должно равняется 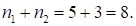
б) метод 4: 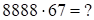
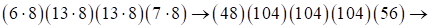 переходим к двучленам
переходим к двучленам 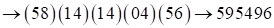 .
.
Ответ: 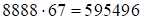 .
.
2 Цифра 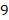 может применятся при нахождении первой и второй, а, следовательно, и третьей частей ответа произведения, в которых первый сомножитель может состоять из других однородных цифр (не девяток), а второй – из произвольных цифр (для случаев
может применятся при нахождении первой и второй, а, следовательно, и третьей частей ответа произведения, в которых первый сомножитель может состоять из других однородных цифр (не девяток), а второй – из произвольных цифр (для случаев 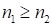 ). Рассмотрим несколько вариантов.
). Рассмотрим несколько вариантов.
? Число 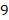 делится на цифру 1-го сомножителя, затем 2-ой сомножитель делится на полученный результат. В результате получаем, как правило, дробное число, целая часть которого и есть первая часть ответа, а первая цифра десятичной дроби – периодическая цифра второй части ответа. Если в результате деления получаем целое число, то от него отнимаем единицу, а в качестве дробной части (второй части ответа) записываем девятки в количестве равном
делится на цифру 1-го сомножителя, затем 2-ой сомножитель делится на полученный результат. В результате получаем, как правило, дробное число, целая часть которого и есть первая часть ответа, а первая цифра десятичной дроби – периодическая цифра второй части ответа. Если в результате деления получаем целое число, то от него отнимаем единицу, а в качестве дробной части (второй части ответа) записываем девятки в количестве равном 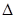 . Третья часть ответа находится, как разность второй и первой частей ответа, причем вторая часть берется с количеством цифр равным
. Третья часть ответа находится, как разность второй и первой частей ответа, причем вторая часть берется с количеством цифр равным 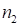 .
.
Примеры:
1) 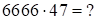
Решение: 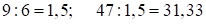 . Первая часть ответа – 31 (
. Первая часть ответа – 31 (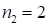 ), а периодическое число второй части
), а периодическое число второй части 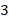 , но
, но 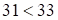 , следовательно сбоя нет. Тогда третья часть ответа равна
, следовательно сбоя нет. Тогда третья часть ответа равна 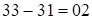 . Итак, ответ:
. Итак, ответ: 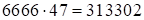 .
.
2) 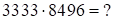
Решение: 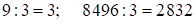 – целое. В этом случае результат записываем как
– целое. В этом случае результат записываем как 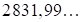 , где
, где 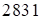 – первая часть ответа, а
– первая часть ответа, а 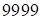 – вторая часть, тогда третья часть
– вторая часть, тогда третья часть 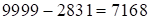 , а т.к.
, а т.к. 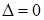 , получаем ответ, состоящий из первой и третьей части.
, получаем ответ, состоящий из первой и третьей части.
Ответ: 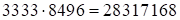 .
.
3) 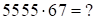
Решение: 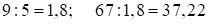
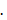 В этом случае
В этом случае 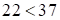 , следовательно, имеем сбой в средней части. Средняя часть ответа
, следовательно, имеем сбой в средней части. Средняя часть ответа 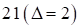 . В этом случае, чтобы найти третью часть ответа находим
. В этом случае, чтобы найти третью часть ответа находим 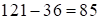 . Итак, ответ:
. Итак, ответ: 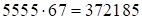 .
.
4) 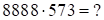
Решение: 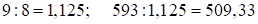 . Средняя часть ответа (виртуальной)
. Средняя часть ответа (виртуальной) 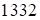 , тогда третья часть:
, тогда третья часть: 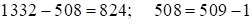 (в случае сбоя отнимается 1).
(в случае сбоя отнимается 1).
Ответ: 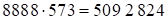 . Средняя часть ответа 2 – число сбоя, т.к.
. Средняя часть ответа 2 – число сбоя, т.к. 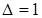 .
.
Составим таблицу результатов деления девятки на различные однозначные цифры 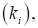 где
где 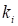 – периодическое число первого сомножителя.
– периодическое число первого сомножителя.
Таблица 1
Деление девятки на однозначные числа
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
9 |
|
|
9 |
4,5 |
3 |
2,25 |
1,8 |
1,5 |
1,285714286… |
1,125 |
|
1 |
Из таблицы 1 следует, что самой неудобной цифрой для этого метода является цифра 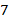 . В этом случае можно воспользоваться другими приемами умножения.
. В этом случае можно воспользоваться другими приемами умножения.
? 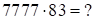
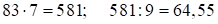 . Но
. Но 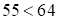 , имеет место сбой. Т.к.
, имеет место сбой. Т.к. 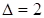 , то средняя часть ответа 54, тогда третью часть (в случае сбоя) находим как разность
, то средняя часть ответа 54, тогда третью часть (в случае сбоя) находим как разность 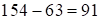 , где
, где 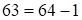 . Итак, ответ:
. Итак, ответ: 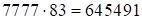 .
.
? Способ
1) 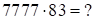
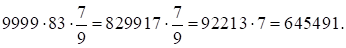 Итак, ответ:
Итак, ответ: 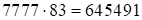 .
.
2) 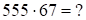
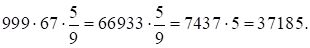 Итак, ответ:
Итак, ответ: 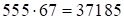 .
.
Замечание: можно использовать при нахождении ответа, первый сомножитель, состоящий из единиц в количестве 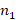 , при умножении его на второй сомножитель, а затем результат произведения умножим на цифру первого сомножителя. Но умножения с помощью девяток – более простой вариант, особенно для случаев, когда второй сомножитель трехчлен, четырёхчлен и т.д. (
, при умножении его на второй сомножитель, а затем результат произведения умножим на цифру первого сомножителя. Но умножения с помощью девяток – более простой вариант, особенно для случаев, когда второй сомножитель трехчлен, четырёхчлен и т.д. (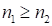 ).
).
Заключение
Обзор различных методов указанных произведений двух сомножителей позволяет в различных случаях применять упрощенные способы любых аналогичных произведений. (Некоторые методы будут рассмотрены в приложениях 1 и 2 к данной статье). Кроме того, методы могут быть актуальны в связи с процессами, разворачивающимися в пространстве Земли и космоса, и переходом в новую частотную среду обитания [4], где все технические средства могут выйти из строя [5].
Библиографическая ссылка
Селиверстова И.Ф. О НЕКОТОРЫХ СПОСОБАХ УМНОЖЕНИЯ // Научное обозрение. Фундаментальные и прикладные исследования. 2022. № 1. ;URL: https://scientificreview.ru/ru/article/view?id=100 (дата обращения: 01.03.2026).