Научный журнал

Научное обозрение. Фундаментальные и прикладные исследования

Цель статьи: применяя рассмотренные ранее способы нахождения произведения двух сомножителей, указанные в работах [1,2,3], находить ответы произведения при различных вариациях количества однородных периодических цифр первого сомножителя по известному ответу произведения какого-либо одного из них.

Введение

В работе рассматриваются различные методы составления ответов произведения двух сомножителей, вторые из которых неизменны (двучлены, трехчлены, …), а первые могут иметь различные количества однородных цифр, если известен ответ какого-либо одного (базового) из них. Методы нахождения базовых произведений приведены в статье автора «О некоторых способах умножения» [1].

Материалы и методы исследования

В статье используются арифметические и алгебраические методы нахождения различных произведений.

Результаты исследований и их обсуждение

Рассмотрим нахождение произведений, первый сомножитель у которых состоит из девяток, когда 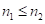при различных количествах 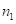, если известно произведение одного из них (*), на один и тот же второй сомножитель.

Примеры:

Дано (*) .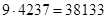

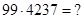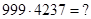Найти 1) ; 2) ; 3) .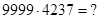

Решение:

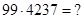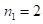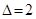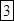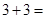
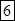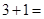
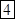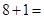
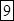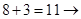
1) Решение:, . Для нахождения произведения (1), цифры ответа произведения (*) пошагово суммируем справа налево (результаты каждого шага помещаем в квадрат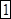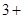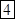): ; ; ; ; ?. ?=. Индексы здесь и далее учитываются как обычно. Цифры в ответе, везде в подобных случаях, записываются в обратном порядке, их получения.

Ответ: .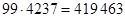

2) 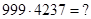Решение: здесь суммирование цифр ответа (*) производится пошагово справа налево в количествах 1, 2, 3, 3, 3, 2, 1. Получим: ; ; ; ?. ?=?. ??; ?=.

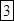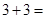
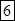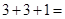
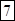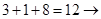
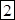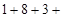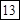
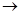
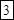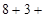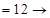
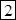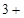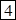Ответ: .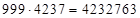

3) 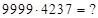Решение: здесь в ответе (*) суммирование цифр производится последовательно в количествах 1, 2, 3, 4, 3, 2, 1 справа налево. Получим:

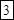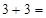
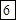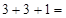
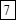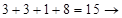
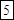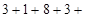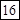
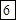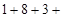; ; ; ?. ?=?; ?=13 ?; ?=?; ?=.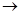

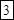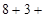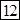
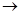
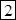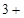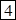Ответ: .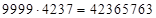

При дальнейшем увеличении числа девяток в первом сомножителе, девятками заполняется средняя часть ответа в количестве .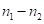

Пример: 1) 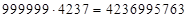. Решение: первая и третья части ответа те же что и в случае 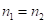. Вторая часть 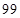, т. к. 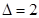. Можно за базовое произведение взять произведение сомножителей, когда .

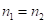Пример, (*) .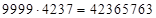

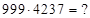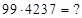Найти: 1) ; 2) ; 3) .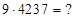

1) 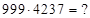Решение: 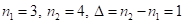. Первая и третья части сохраняются как в (*) в количестве цифр равном 3 каждая (как у наименьшего сомножителя), т.е. 423 – первая, а 763 – третья части ответа. Среднюю часть находим, суммируя цифры: последнюю цифру первой части (6) ответа и первую с третьей части (5), а затем отнимаем от суммы периодическое число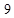, т.е. 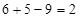– средняя часть данного произведения. Итак, ответ: .

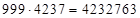2) 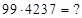Решение: 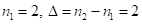, тогда из 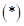первая часть ответа – 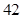, а третья – (первые и последние двучлены ответа (*)). Найдем среднюю часть. Для этого в ответе (*) суммируем двучлены: последний первой части ответа и первый третьей части, т.е. 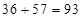. От 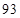отнимаем периодическое число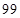 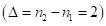, но т.к. 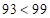, то занимаем единицу из предыдущего разряда первой части ответа. Получим 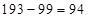, а первая часть ответа будет равна 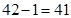. Итак, ответ: .

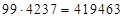3) 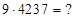Решение: 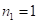. Следовательно, первая и третья части – одночлены – крайние цифры ответа (*), т.е. 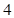и 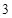. Для нахождения средней части суммируем в (*) (т.к. 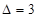) ближайшие к центру трёхчлены и отнимаем 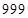. Получим: 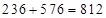; 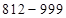. В этом случае опять занимаем единицу у предыдущего старшего разряда в ответе (*). Получим: 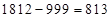, а первая часть ответа становится на единицу меньше: 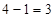. Итак, ответ: .

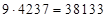Рассмотрим случаи, когда в базовом произведении первый сомножитель может состоять из другого количества девяток: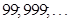

Примеры:

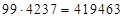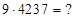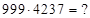Дано (*): . Найти: 1) 2) 3)

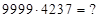
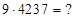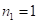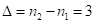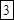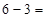
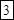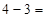
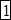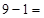
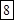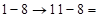
1) Решение: , . Последняя цифра ответа (*) – сохраняется. А далее от цифр предыдущего разряда отнимаем пошагово предыдущее найденное число. Получим: ; ; ; ; 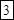(единицу заняли у предыдущей цифры соседнего разряда);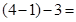 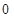. Ответ: .

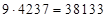2) 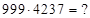Решение: здесь можно найти произведение 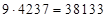и прибавить его к ответу 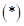, учитывая необходимый сдвиг разрядов, т.е.

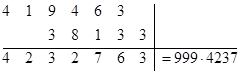
Можно воспользоваться другими, указанными ранее способами умножения.

3) 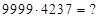Решение: здесь самое простое – непосредственно записать ответ по правилу [1]. Получим ответ: 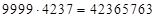. Можно воспользоваться другим способом.

а) Пусть (*) 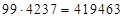. Найти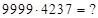

Решение: из (*) 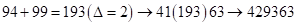. Здесь первая и третья части – двучлены, а в искомом произведении четырехчлены. Неизвестные цифры обозначим неизвестными 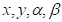. Тогда искомые части примут вид 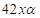и 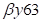– первая и третья части ответа, а среднее число (виртуальное) искомого произведения – 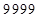. Тогда

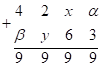
то есть 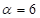; ; 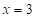; 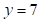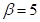. Искомый ответ: 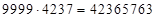(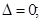средней части нет).

б) Пусть (*) 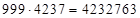. Найти 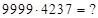Решение: здесь неизвестны две цифры искомого ответа – последняя в первой части и первая в – третьей. Обозначим их соответственно 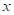и 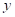, т.е. 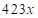– первая часть ответа, а 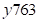– третья часть. Средняя часть ответа 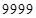(виртуальное) тогда

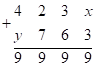
то есть 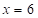; 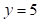. Получим: первая часть ответа 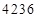, третья – 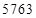, а 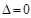, средней части нет. Итак, ответ: .

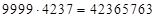Пусть дано 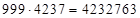. Найти 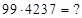Решение: в этом случае от результата произведения (*) надо отнять результат 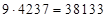, расположив советующим образом порядки, а именно:

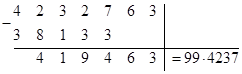
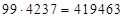. Или просто применить обычные правила умножения [1], где действия производятся главным образом с двумя сомножителями: 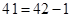, 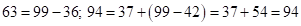– средняя часть ответа. А произведение, когда 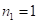(девятке) можно быстро подсчитать разными способами. Наиболее удобный – разделение на десятки и единицы (способ 7, [1]).

Пример: найти 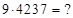Умножая каждую цифру второго сомножителя, пошагово на 9, десятки и единицы произведения записываем раздельно, получим: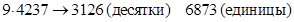 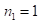, следовательно, первая и третья части ответа – одночлены. Выделим их: 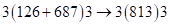. Итак, ответ: .

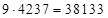В работе [3] рассмотрены случаи нахождения ответов промежуточных произведений по базовым произведениям 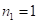с и с 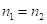при одном и том же втором сомножителе (произвольном), а первый может состоять из произвольных однородных цифр. Приведем примеры таких произведений и дополним их случаями, когда базовым произведением может быть произвольное из них. Рассмотрим случаи, когда второй сомножитель, главным образом, – трехчлен.

а) Число второй части ответа – без сбоя.

Пусть (*) 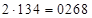, здесь 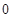впереди добавлен для формализации ответа, в котором количество цифр должно быть равно .

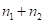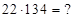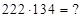Найти 1) 2) 3)

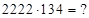
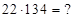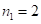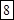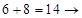
1) Решение: здесь . Ответ находим пошаговым суммированием соседних цифр ответа (*), начиная (как и везде) с конца. Имеем из (*): ; 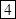?; ?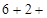=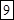; 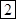. Начало ответа, как обычно, записываем с конца 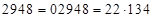– ответ.

2) 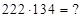Здесь 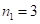. Производим пошаговое суммирование соседних цифр ответа (*) в количествах 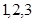, справа налево, а затем 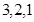слева направо. Получим: ; ?; ? ?. ?= ; ; .

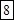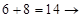
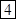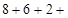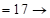
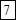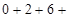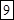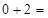
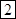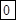Ответ: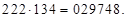

3) 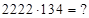В таких случаях всегда проще найти среднюю часть ответа произведения (3) и поместить ее в среднюю часть ответа произведения (2). Средняя часть: 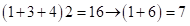– периодическое число, а 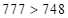, следовательно, сбоя нет. Количество цифр в ответе второй части равно 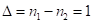, т.е. вторая часть ответа (3) равна 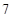первая часть 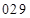, третья – 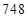– из ответа (2) или 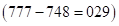. Получим ответ: .

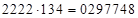Рассмотрим произвольные базовые варианты этих сомножителей:

Дано (*) 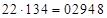. Найти 1) 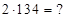2)

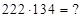
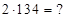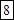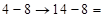
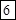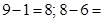
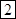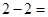
1) Решение: из (*) имеем ; . (здесь единица занята из предыдущего разряда). Его цифра стала ; 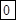. Получим 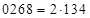– ответ.

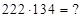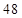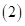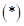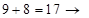
2) Решение: из (*) найдем третью часть ответа: – две последние цифры т.к. они совпадают (по наименьшему количеству цифр, входящих в первый сомножитель (*) и ). Затем находим первую цифру третьей части из : 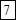. Тогда третья часть ответа (2) – 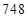. Первую часть находим как разность второй (виртуальной) и третьей частей, т.е. 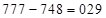. Итак, имеем 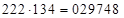– ответ.

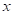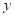Можно применить другой способ. Ответ произведения (*) содержит крайние (внешние) двучлены первой и третьей части ответа (2)Для формализации трехчленов ответа (2) введем неизвестные и , т.е. первая часть 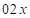, а третья – 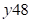. Их сумма должна равняться среднему числу ответа 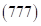, т. е.

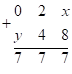
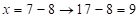; 1 – заняли у предыдущего разряда среднего числа ответа, а 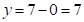. Получим: первая часть – 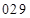, третья часть – 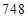. Ответ: .

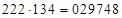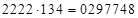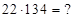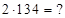Рассмотрим ход процесса в обратном порядке. Дано (*)1 . Найти 1) 2) Средняя часть в (*)1 – 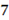– без сбоя.

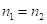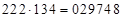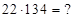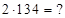Решение: перейдем от (*)1 к (*)2, где (убрали среднюю часть из (*)1). Дано (*)2 . Найти 1) 2) Решение. Здесь – 7 первая цифра третьей части ответа (*)1 – 748. Чтобы найти первую часть ответа суммируем в (*)2 первую часть и первую цифру третьей части 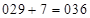, а затем от результата отнимаем среднее число 7 (так как 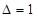), получим: 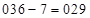– первая часть ответа. А т.к. 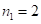, то последние две цифры ответа (*)1 сохраняются. Получим 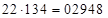– ответ.

2) 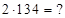Решение: 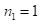. В ответе здесь сохраняется последняя цифра 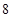из (*)2. А т. к. 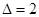, имеем: 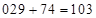, 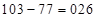– первая часть ответа. Ответ: .

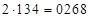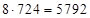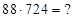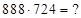Пример: Дано (*) . Найти 1) ; 2) ; 3) 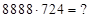Средняя часть ответа перемножаемых сомножителей – со сбоем.

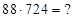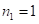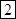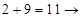
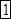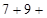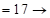
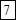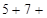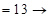
1) Решение: ответ находим методом пошагового суммирования соседних цифр (*) справа налево: из (*) последняя цифра 2 неизменна (). Получим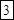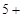: ; ?; ? ?. ? ?; ? = . Ответ: .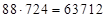

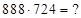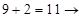
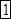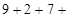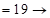
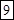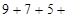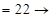
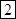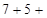
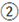
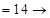
2) Аналогично ранее указанному, метод суммирования производится справа налево в порядке 1, 2, 3, а затем слева направо в порядке 3, 2, 1. Получим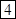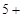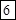: ; ?; ? ?. ? ?; ?. ?=. Ответ: .

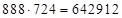В этом случае (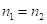) получим две части ответа: первую – 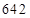и третью – 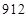. Средняя часть равно 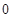, т.к. 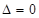. Дальнейшее увеличении 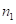приведет к появлению чисел второй части в количестве, равном 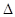. Так как в этом случае имеет место сбой, то сначала во второй части ответа появляется цифра сбоя и одновременно увеличивается на единицу первая часть, а с увеличением 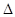пошагово увеличивается количество периодических цифр второй части ответа. Итак, можем записать: 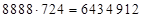, здесь средняя часть ответа 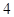– число сбоя (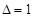), , 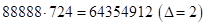средняя часть 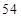и т.д. Первая часть увеличивается на единицу начиная с 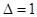, т.е. .

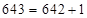Зная ответ для 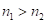, всегда автоматически можно его записать для случая .

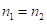3) Найдем: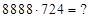

Ответ для случаев 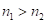можно найти и путем суммирования цифр ответа (*), [1].

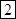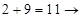
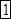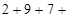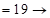
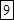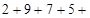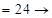
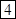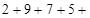
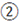
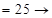
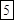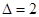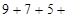
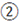
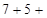
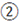
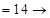
Решение: из ответа (*) имеем: ; ?; ??. ? ?; ? (суммируем все цифра ответа (*) дважды, т.к. ) ? ; ?; 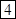?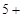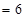. Тогда получим .

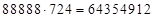Нахождение ответов произведений с одинаковым вторым сомножителем, когда количество цифр первого сомножителя меньше, чем базового.

Дано (*) 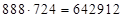. Найти 1) 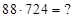2)

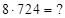
1) 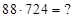Решение: цифры последней части ответа (*) в количестве 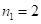, т.е. 12 – не меняются. Затем суммируем первую часть с первой цифрой третьей части (т.к. 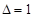) и отнимаем 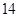(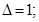4 – цифра сбоя, а единица забирается от первой части ответа). Получим: 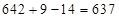. Тогда ответ: .

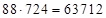2) 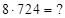Решение: из ответа (*) 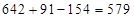, т.к. 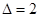, а средняя часть 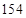, а так как 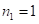, то последняя цифра ответа (*) неизменна. Получим ответ: .

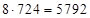Рассмотрим случаи, когда базовым произведением является (*) 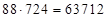. Найти 1) 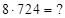2)

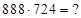
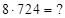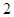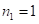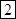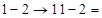
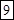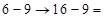
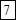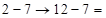
Решение: 1) Здесь применяем метод последовательного вычитания. Последняя цифра из ответа (*) неизменна, т. к. в (1): ; . Здесь, как и всегда в таких случаях единицу занимаем в соседнем предыдущем разряде. ; ; 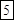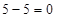. Ответ: .

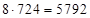2) 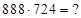Решение: чтобы найти первую и третью части ответа при 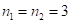, надо найти по три составляющих их цифры. Из ответа (*) имеем в первой части ответа две первые цифры – 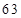, а в третьем две последние – 12. Заменим недостающие цифры неизвестным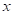и и 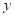, т.е. получим 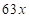и 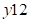соответственно и воспользуемся свойством равенства суммы первой и третьей частей ответа среднему числу 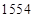(в нашем случае – виртуальному):

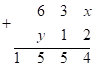
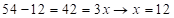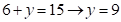где , а . Но 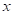– однозначное число поэтому число десятков переходит к предыдущему разряду 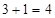. Получаем: первая часть ответа – 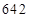, а третья – 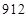. Ответ: .

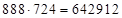Рассмотрим еще один способ вариации ответов произведений при заданном базовом произведении 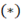независимо от наличия сбоя во второй части ответа.

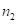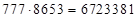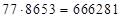Примеры. Пусть – четырёхзначное число. Рассмотрим произведения: 1) ; 2) ; 3) 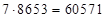. Будем выбирать базовым произведением (*) любое из них и находить ответы остальных, используя метод скобок [3].

1) Пусть (*) 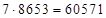. Найти 2)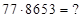

Решение: запишем ответ (*) в виде скобок, полученных пошаговым перемножением 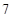на каждую цифру второго сомножителя: 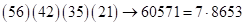– ответ. При получении ответа произведения (2) крайние скобки остаются неизменными. Суммируем цифры двух первых и двух последних скобок: 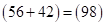и 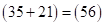. Располагаем 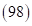и 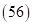между крайними двучленам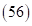и и 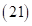. Затем суммируем цифры двух внутренних скобок 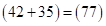и результат помещаем в середине: 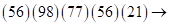(суммируя пошагово) 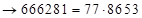– ответ.

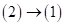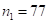Чтобы пойти обратным путем (от к 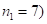, ответ произведения (2) записываем в виде скобок: 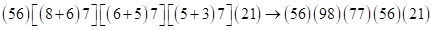. Затем удаляем среднюю скобку, а в соседних (справа и слева от нее) записываем разность цифр второй и первой скобок слева и третьей и четвертой – справа, т.е. 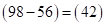и 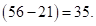Крайние скобки – без перемен. Получим 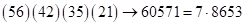– ответ.

2) Дано (*) 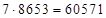. Найти 1)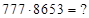

Решение: записываем ответ произведения (*) в виде скобок: 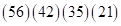. Далее суммируем цифры скобок в последовательности: слева направо в количествах 1, 2, 3, а затем справа налево в количествах 3, 2, 1. Получим:

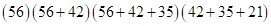
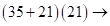
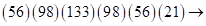
(переходим к двучленам) 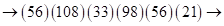еще раз 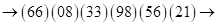пошагово суммируем справа налево 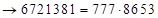– ответ.

В случае обратного перехода (от 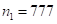к 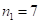) из ответа в виде скобок для произведения (2), т. е. 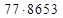, получаем:

,

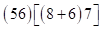
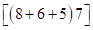
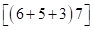
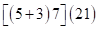
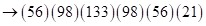далее удаляем скобки, в которых 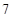умножается на сумму трех цифр. Получим 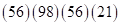, а затем, вместо второй скобки, записываем разность цифр второй и первой скобок 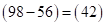, а вместо третьей – разность цифр третьей и четвертой скобок, т.е. 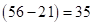. Получим: 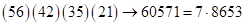– ответ.

3) Дано (*) 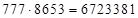. Найти 2)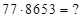

Решение: записываем ответ произведения (*) в виде скобок:

.

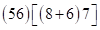
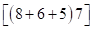
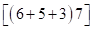
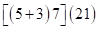
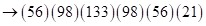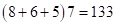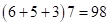Удаляем произведения с суммой трех цифр и , получим 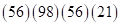. Среднюю скобку для полученного выражения можно найти как разность цифр третьей и первой скобок произведения (*) 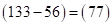или четвертой и шестой скобок, т. к. 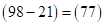. Скобку 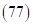помещаем в середину скобок, полученных после удаления произведений трех слагаемых. Получим 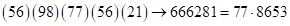– ответ.

Чтобы перейти от ответа произведения с 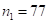к ответу произведения с 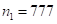надо последовательно просуммировать цифры третьей и первой скобок, а затем третьей и пятой и записать их как третью и четвертую скобки в окончательное выражение. Получим 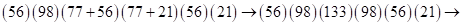(переходим к двучленам в скобках) 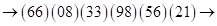(пошагово суммируем) 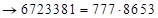– ответ.

При необходимости на практике можно использовать любой из этих методов.

Методы могут быть полезны при проведении расчётов с большими массивами данных (в торговых операциях, научных исследованиях и так далее), особенно в связи с изменениями, идущими сейчас в процессе Великого Перехода [4,5] и, в частности, с выходом из строя связи, всех высокочастотных технологических изделий [6-9].

Заключение

Указанные методы расширяют возможности нахождения произведений двух сомножителей в случаях, когда первый сомножитель состоит из различного количества однородных цифр, а второй – из произвольных, но неизменных цифр в каждой группе преобразования.